Тригонометрические функции. Синус

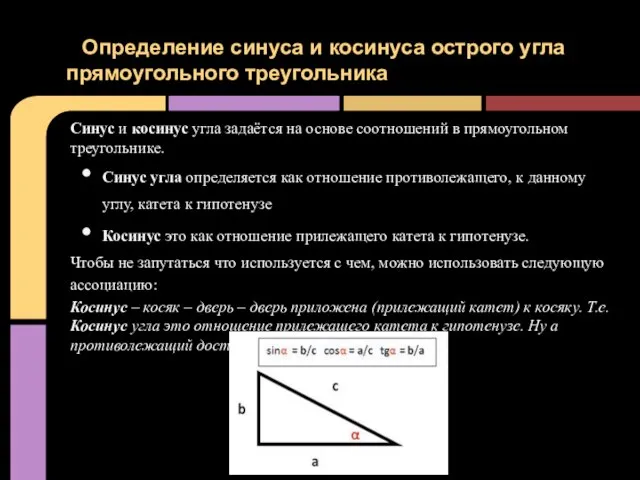
Синус и косинус угла задаётся на основе соотношений в прямоугольном треугольнике.
Синус угла определяется как отношение противолежащего, к данному углу, катета к гипотенузе
Косинус это как отношение прилежащего катета к гипотенузе.
Чтобы не запутаться что используется с чем, можно использовать следующую ассоциацию:
Косинус – косяк – дверь – дверь приложена (прилежащий катет) к косяку. Т.е. Косинус угла это отношение прилежащего катета к гипотенузе. Ну а противолежащий достаётся синусу.
Определение синуса и косинуса
Определение синуса и косинуса острого угла прямоугольного треугольника

Вспомни синусы некоторых углов. Посмотри фильм.

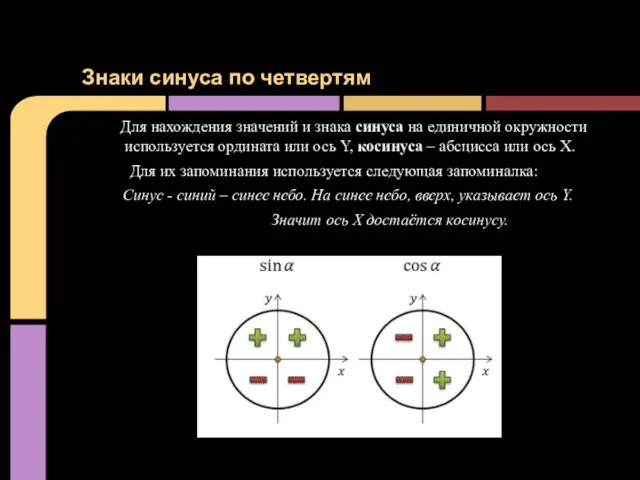
Для нахождения значений и знака синуса на единичной окружности используется ордината или ось Y, косинуса – абсцисса или ось X.
Для их запоминания используется следующая запоминалка:
Синус - синий – синее небо. На синее небо, вверх, указывает ось Y.
Значит ось X достаётся косинусу.
Значения и знаки синуса и косинуса
Значения и знаки синуса и косинуса
Знаки синуса по четвертям

Областью определения функции синус является множество всех действительных чисел, т. е.
D(y) = R.
Каждому действительному числу х соответствует единственная точка единичной окружности Рx, получаемая поворотом точки Р0(1; 0) на угол, равный х радиан. Точка Рx имеет ординату, равную sinх. Следовательно, для любого х определено значение функции синус.
Свойства функции синус

Свойства функции синус
2. Множеством значений функции синус является промежуток [-1; 1], т. е. Е(у) = [-1;1]
Это следует из определения синуса: ордината любой точки единичной окружности удовлетворяет условию -1≤y≤1

Пусть точка Рx получена при повороте точки Р0 на x радиан, а точка Р-x получена при повороте точки Р0 на -х радиан.
Треугольник ОРxР-x является равнобедренным; ON — биссектриса угла РxОР-x, значит, ON является медианой и высотой, проведенной к стороне РxР-x. Следовательно, PxN = Р-xN, т. е. ординаты точек Рx и Р-x одинаковы по модулю и противоположны по знаку. Это означает,
что sin(-x) = -sinx.
Свойства функции синус
3. Функция синус является нечетной, т. е. для любого x∈R выполняется равенство sin⁡(-x)=-sin⁡x

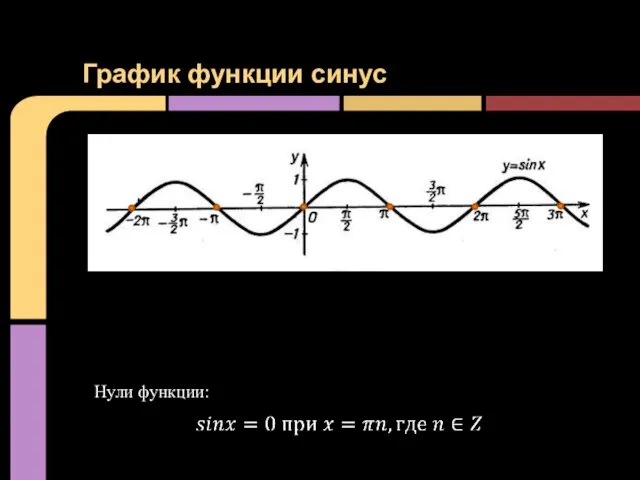
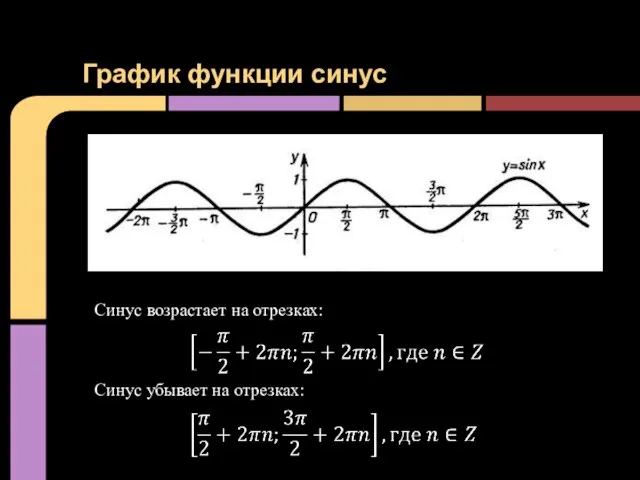
График функции синус
Нули функции:

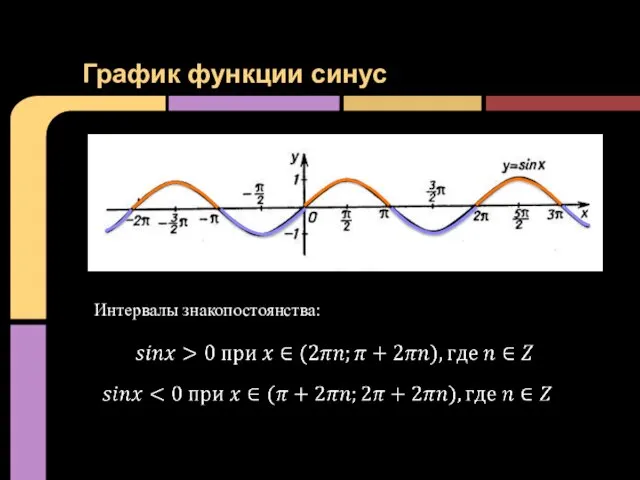
График функции синус
Интервалы знакопостоянства:

График функции синус
Синус возрастает на отрезках:
Синус убывает на отрезках: