Ты, я и тригонометрия!

Счастливая случайность выпадает лишь на долю подготовленных умов.
Луи Пастер

Дидактические цели проекта:
Обобщить и систематизировать знания учащихся о тригонометрических функциях;
Развить творческую активность;
Расширить кругозор учащихся
Развить навыки самостоятельной работы и работы в группе;
Сформировать учебные навыки по работе с информационными источниками;

Задачи проекта:
Научить самостоятельно искать, изучать и обобщать учебный материал;
Научить планировать, проводить анализ построения графиков тригонометрических функций;
Выполнять построения графиков тригонометрических функций;

Направляющие вопросы:
Основополагающий вопрос:
В чём загадка тригонометрических функций?
Проблемные вопросы:
Чем отличаются графики тригонометрических
функций от других графиков функций?
В чём сходство и различие тригонометрических
Функций?
Обратные тригонометрические функции, какие они? Почему так называют?

Учебные вопросы:
Что такое функция?
Что такое тригонометрическая функция?
Какими свойствами обладают
тригонометрические функции?
Обратные тригонометрические функции, как
получить их и что они из себя
представляют?
Как построить графики этих функций?

Что мы будем делать?
Проект рассчитан на изучение темы в большей мере самостоятельно: поэтапная подготовка к каждому уроку, развёрнутые ответы на проблемные вопросы, изучение различной литературы, самоанализ выполненных работ, обсуждение с одноклассниками и работа в группах.

Работа в группах!
Класс делится на 4 группы. Группа синусов, косинусов, тангенсов и котангенсов. Каждая группа готовит девиз, небольшое стихотворение об участниках и развёрнутый материал по заданной функции: определение, происхождение (история), график, простейшие свойства.
Оценивается: правильность, точность, чёткость, творчество.
Желаю успехов!

А теперь представляю вам краткий курс изучения нашей темы:

Задача тригонометрии.
Определение сторон и углов треугольника,
когда уже известны некоторые из них.
Определение.
Тригонометрические функции - это
неалгебраические функции, устанавливающие
зависимость между сторонами и углами
треугольника. Тригонометрические функции угла α
определяются при помощи числовой окружности, а
также из прямоугольного треугольника (для острых
углов).
Тригонометрические функции

Непрерывность.
y=Sin x и y=Cos x – непрерывные функции.
2. Чётность, нечётность.
Sin (-x)=-Sin x – нечётная функция
Cos (-x)=Cos x – чётная функция
Tg (-x)=-Tg x – нечётная функция
Ctg (-x)=-Ctg x – нечётная функция
3. Периодичность.
Sin (x+2П)=Sin x
Cos (x+2П)=Cos x
Tg (x+П)=Tg x
Ctg (x+П)=Ctg x
Простейшие свойства:

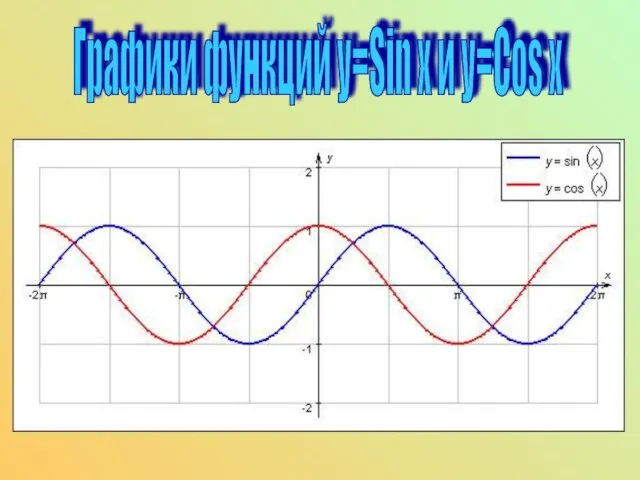
Графики функций y=Sin x и y=Cos x

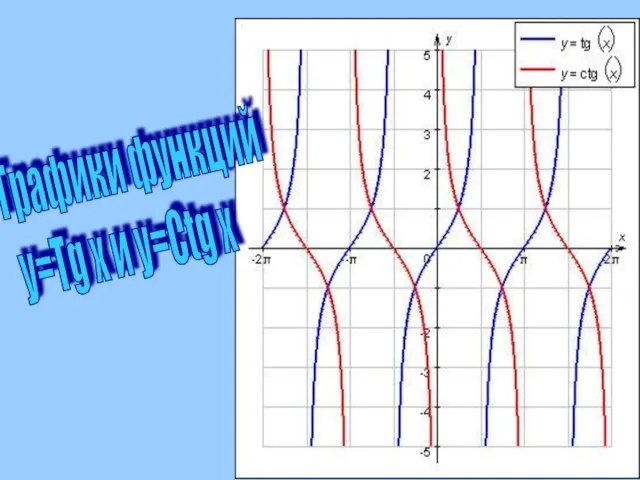
Графики функций y=Tg x и y=Ctg x

Первые Тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции встречающиеся уже в III веке до н.э. в работах великих математиков – Евклида, Архимеда, Апполония Пергского. Древнегреческие астрономы успешно решали отдельные вопросы из тригонометрии, связанные с астрономией.
История развития!

В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты. Отрезок CB он назвал ардхаджива (ардха –половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. (синус)
Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке Аль - Батани (850-929) и Абу-ль-Вефа Мухамед-бен Мухаммед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604.

В середине 9 века среднеазиатский ученый аль-Хорезми написал сочинение «Об индийском счете». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Постепенно тригонометрия органически вошла в математический анализ, механику, физику и технические дисциплины.