Содержание
- 2. Многопроцессорные системы с распределенной памятью с общей памятью Гибридные Модель выполнения программ Методы взаимодействия процессов Методы
- 3. Транспьютерная материнская плата МТБ-8 Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В.
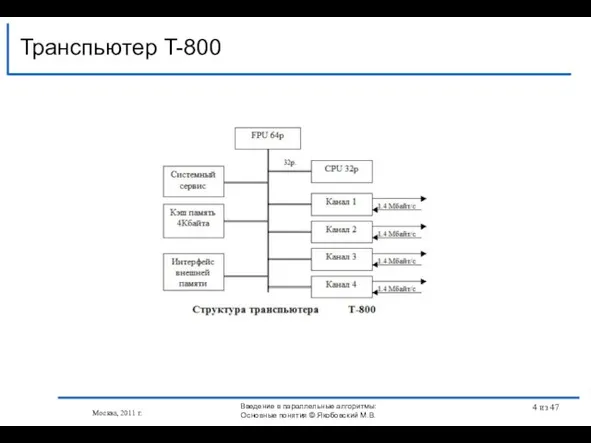
- 4. Транспьютер T-800 Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В. из 47
- 5. Транспьютерная материнская плата МТБ-8 Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В.
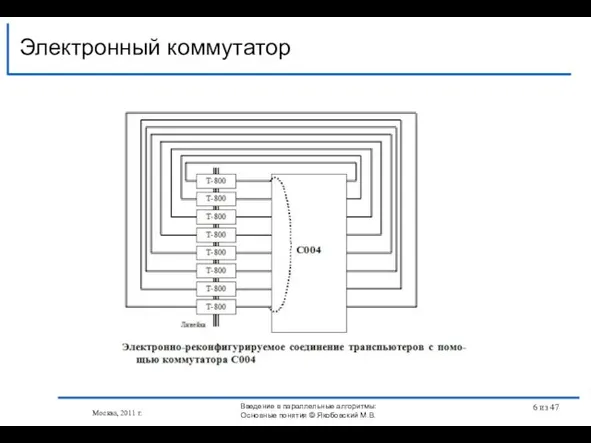
- 6. Электронный коммутатор Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В. из 47
- 7. Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В. из 47
- 8. Узел с общей памятью – два процессора Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия
- 9. Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В. из 47
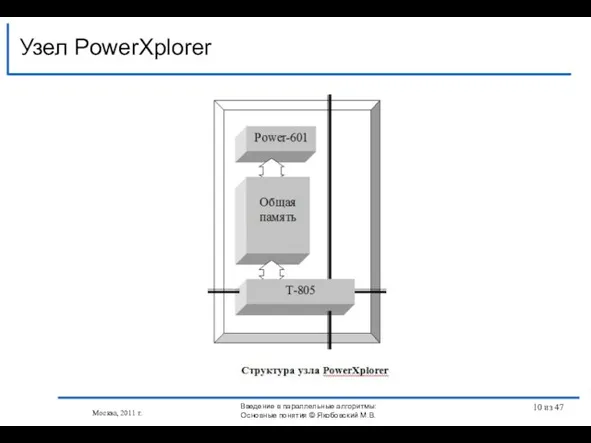
- 10. Узел PowerXplorer Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В. из 47
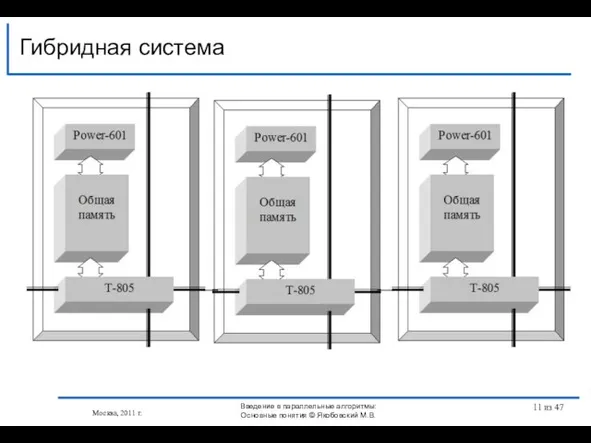
- 11. Гибридная система Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В. из 47
- 12. Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В. из 47
- 13. Плата и 4 модуля Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский М.В.
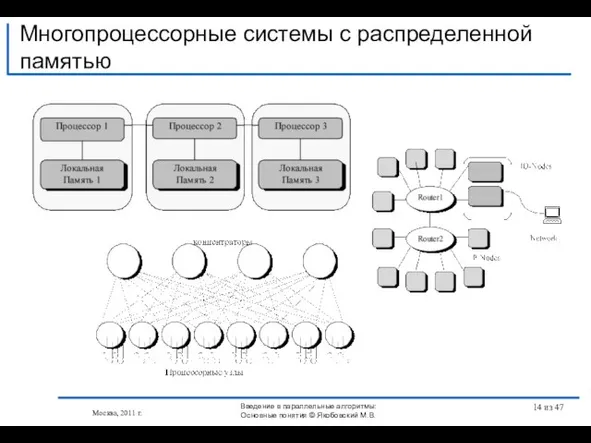
- 14. Многопроцессорные системы с распределенной памятью Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский
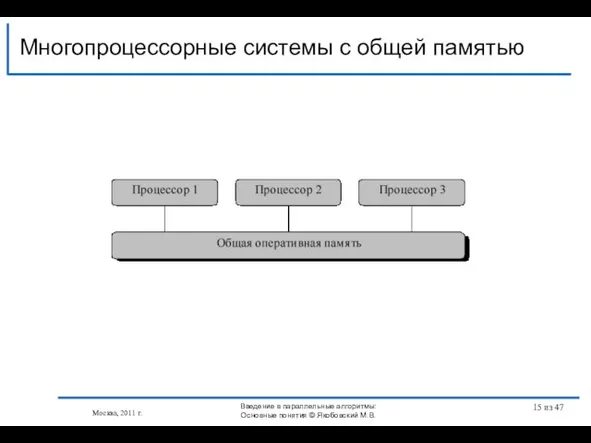
- 15. Многопроцессорные системы с общей памятью Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия © Якобовский
- 16. При запуске указываем число требуемых процессоров Np и название программы На выделенных для расчета узлах запускается
- 17. Работа начинается с запуска одной программы При необходимости программа порождает новые процессы, эти процессы: Обладают собственными
- 18. Синхронный метод Send(адрес данных, размер, номер процессора) Recv(адрес данных, размер, номер процессора) Асинхронные методы Небуферизованный ASend(адрес
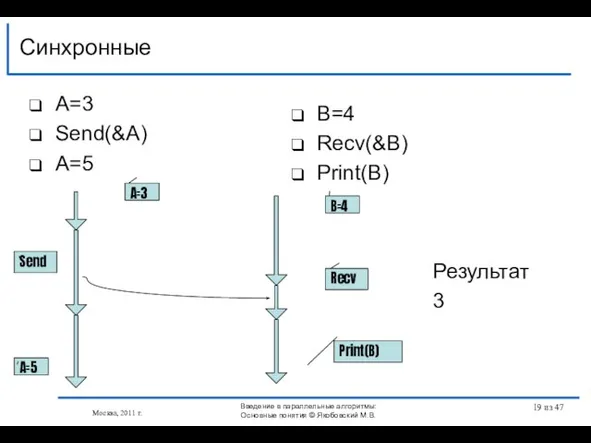
- 19. A=3 Send(&A) A=5 Синхронные Москва, 2011 г. B=4 Recv(&B) Print(B) Send Recv Print(B) A=5 B=4 A=3
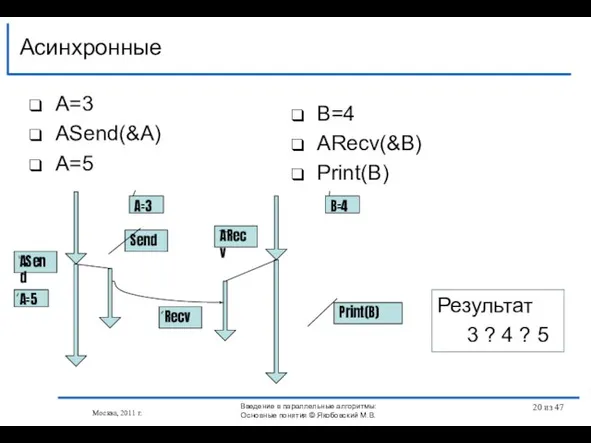
- 20. A=3 АSend(&A) A=5 Асинхронные Москва, 2011 г. B=4 АRecv(&B) Print(B) Send ASend Recv ARecv Print(B) A=5
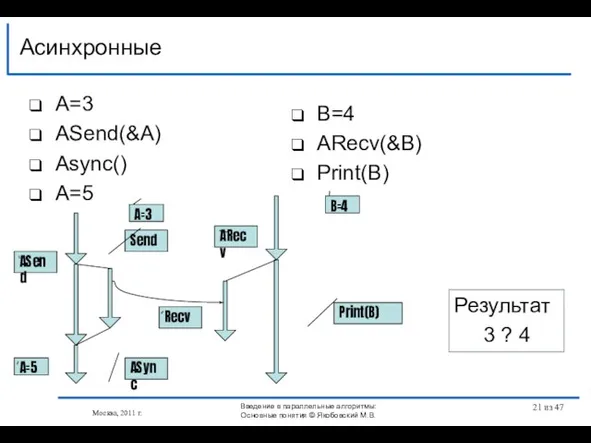
- 21. A=3 АSend(&A) Async() A=5 Асинхронные Москва, 2011 г. B=4 АRecv(&B) Print(B) ASync Send ASend Recv ARecv
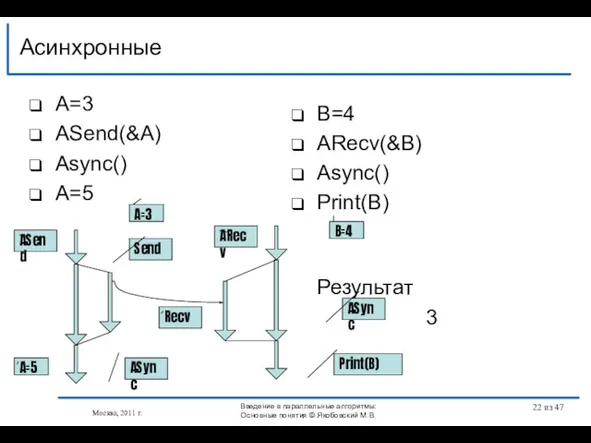
- 22. A=3 АSend(&A) Async() A=5 Асинхронные Москва, 2011 г. B=4 АRecv(&B) Async() Print(B) Результат 3 ASync Send
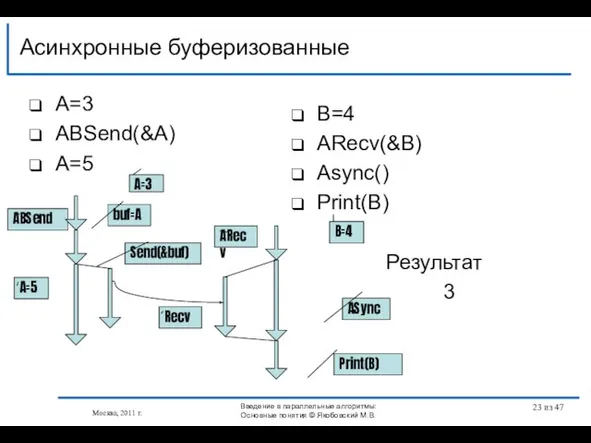
- 23. A=3 АBSend(&A) A=5 Асинхронные буферизованные Москва, 2011 г. B=4 АRecv(&B) Async() Print(B) Результат 3 Send(&buf) ABSend
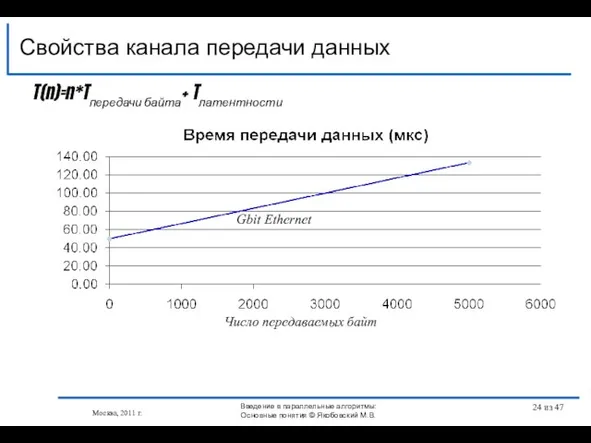
- 24. Свойства канала передачи данных Москва, 2011 г. Gbit Ethernet Число передаваемых байт Введение в параллельные алгоритмы:
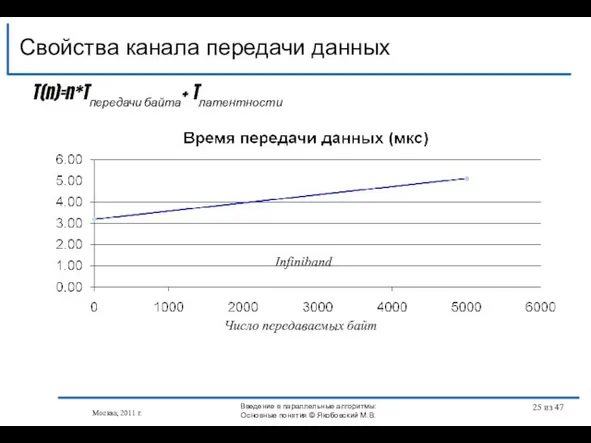
- 25. Свойства канала передачи данных Москва, 2011 г. T(n)=n*Tпередачи байта+ Tлатентности Число передаваемых байт Infiniband Введение в
- 26. Целочисленная неотрицательная переменная Две атомарные операции, не считая инициализации V(S) Увеличивает значение S на 1 P(S)
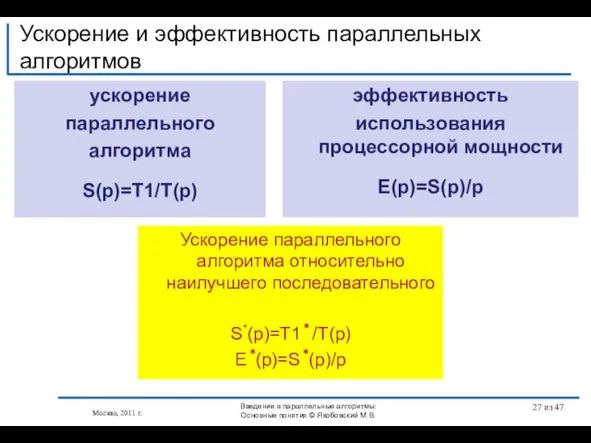
- 27. ускорение параллельного алгоритма S(p)=T1/T(p) Ускорение и эффективность параллельных алгоритмов Москва, 2011 г. Ускорение параллельного алгоритма относительно
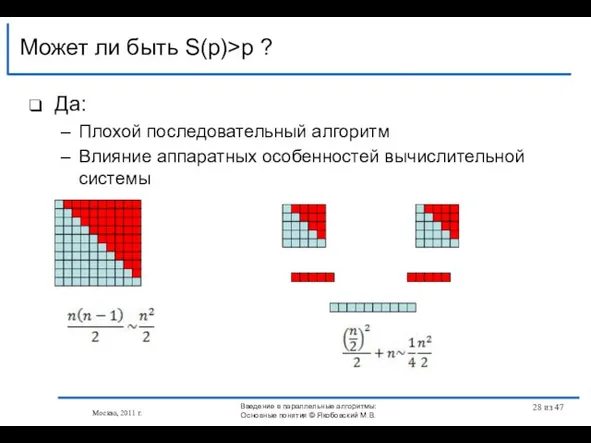
- 28. Да: Плохой последовательный алгоритм Влияние аппаратных особенностей вычислительной системы Может ли быть S(p)>p ? Москва, 2011
- 29. Да Если первый алгоритм позволяет использовать больше процессоров, чем второй. Самый эффективный алгоритм – использующий один
- 30. Все элементарные операции (+ - * / ) выполняются за время τс Все операции выполняются точно,
- 31. S=1; a=1; for(i=1;i { a=a*x/i; S=S+a; } Последовательный алгоритм T1= 3nτс Москва, 2011 г. Введение в
- 32. Параллельный алгоритм Вычислить для всех i =1,…,n : xi Вычислить для всех i =1,…,n : i!
- 33. Для вычисления xi воспользуемся методом бинарного умножения x 1 x2 2 x3 x4 3 x5 x6
- 34. Параллельное вычисление всех требуемых i! ? ? Москва, 2011 г. Введение в параллельные алгоритмы: Основные понятия
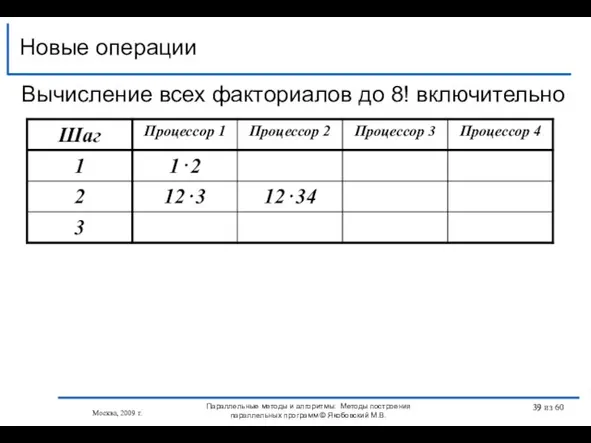
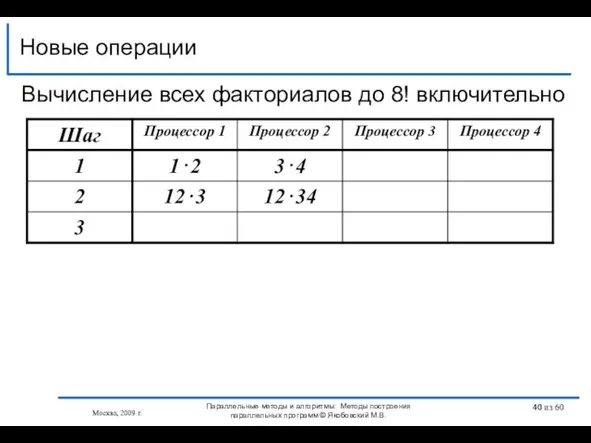
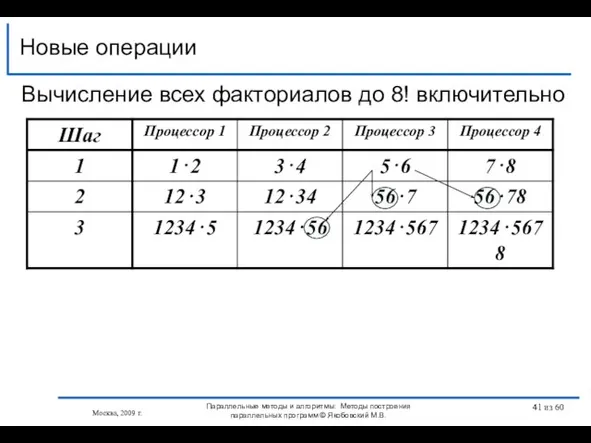
- 35. 4 1⋅2⋅ 3⋅4⋅ 5⋅6⋅ 7⋅8⋅9⋅10⋅ 11⋅12 ⋅13⋅14⋅ 15⋅16=16! 3 1⋅2⋅ 3⋅4⋅ 5⋅6⋅ 7⋅8 9⋅10⋅ 11⋅12 ⋅13⋅14⋅
- 36. Для вычисления i! воспользуемся аналогичным методом 4 1⋅2⋅ 3⋅4⋅ 5⋅6⋅ 7⋅8⋅9⋅10⋅ 11⋅12 =12! 3 1⋅2⋅ 3⋅4⋅
- 37. Для вычисления i! воспользуемся аналогичным методом 4 1⋅2⋅ 3⋅4⋅ 5⋅6⋅ 7⋅8⋅9⋅10⋅ 11⋅12 ⋅13⋅14=14! 3 1⋅2⋅ 3⋅4⋅
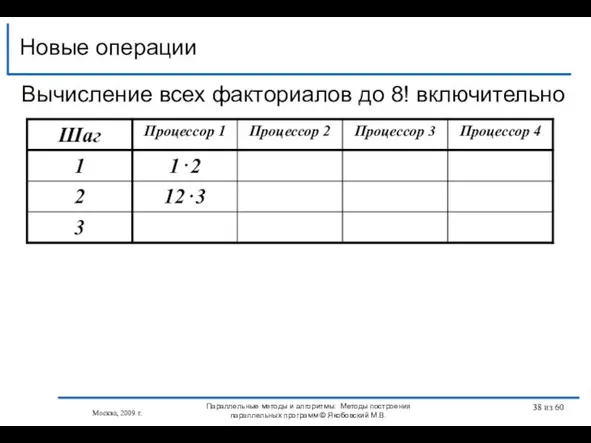
- 38. Новые операции Москва, 2009 г. Параллельные методы и алгоритмы: Методы построения параллельных программ © Якобовский М.В.
- 39. Новые операции Москва, 2009 г. Параллельные методы и алгоритмы: Методы построения параллельных программ © Якобовский М.В.
- 40. Новые операции Москва, 2009 г. Параллельные методы и алгоритмы: Методы построения параллельных программ © Якобовский М.В.
- 41. Новые операции Москва, 2009 г. Параллельные методы и алгоритмы: Методы построения параллельных программ © Якобовский М.В.
- 42. Новые операции Москва, 2009 г. Параллельные методы и алгоритмы: Методы построения параллельных программ © Якобовский М.В.
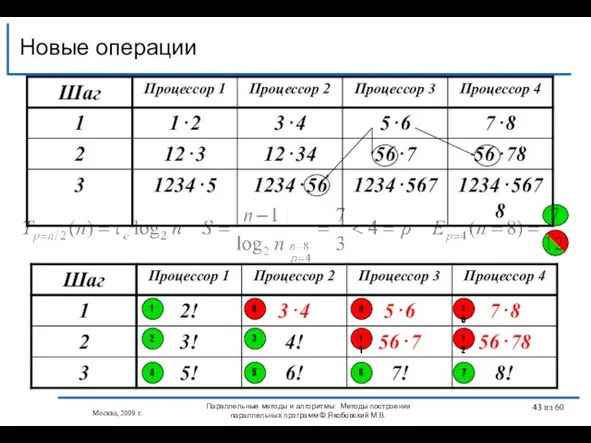
- 43. Новые операции Москва, 2009 г. Параллельные методы и алгоритмы: Методы построения параллельных программ © Якобовский М.В.
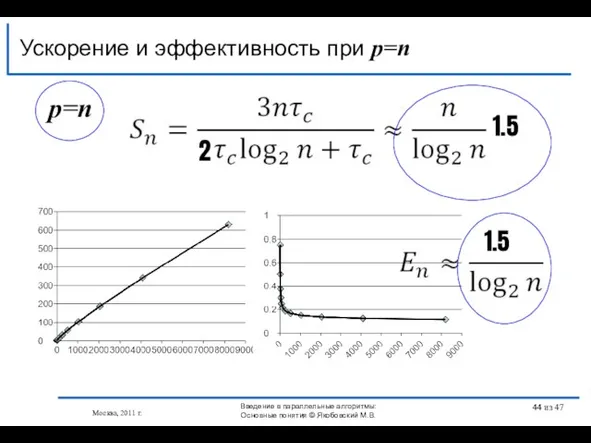
- 44. p=n Ускорение и эффективность при p=n 2 1.5 1.5 Москва, 2011 г. Введение в параллельные алгоритмы:
- 45. Определены классы рассматриваемых вычислительных систем Представлены модели параллельных программ Представлен ряд способов организации взаимодействия последовательных процессов
- 46. Сколько нужно процессоров для вычисления суммы ряда за время 2 + q , где q –
- 48. Скачать презентацию
























 Презентация на тему Основные инфекционные заболевания и их профилактика
Презентация на тему Основные инфекционные заболевания и их профилактика Митральные пороки
Митральные пороки  Влияние компьютерных игр на здоровье младших школьников и определение компьютерной зависимости
Влияние компьютерных игр на здоровье младших школьников и определение компьютерной зависимости Презентация на тему Пальчиковая гимнастика
Презентация на тему Пальчиковая гимнастика  “Мастерская для инноваций”
“Мастерская для инноваций” В каких странах говорят на английском языке?
В каких странах говорят на английском языке? В ожидании Рождества. Фотоальбом
В ожидании Рождества. Фотоальбом В.Б. Тарасов МГТУ им. Н.Э.Баумана, Кафедра «Компьютерные системы автоматизации производства» e-mail:
В.Б. Тарасов МГТУ им. Н.Э.Баумана, Кафедра «Компьютерные системы автоматизации производства» e-mail:  Административная ответственность
Административная ответственность МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ ВЕРБАЛЬНЫХ И НЕВЕРБАЛЬНЫХ ЕДИНИЦ В ДИАЛОГЕ II Б. ДЕЙКТИЧЕСКИЕ ЖЕСТЫ И РЕЧЕВЫЕ АКТЫ Крейдлин Г. Е. (РГГУ,
МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ ВЕРБАЛЬНЫХ И НЕВЕРБАЛЬНЫХ ЕДИНИЦ В ДИАЛОГЕ II Б. ДЕЙКТИЧЕСКИЕ ЖЕСТЫ И РЕЧЕВЫЕ АКТЫ Крейдлин Г. Е. (РГГУ,  Технология как часть общечеловеческой культуры
Технология как часть общечеловеческой культуры Коммуникационные технологии
Коммуникационные технологии  Атмосфера: значение, строение, изучение
Атмосфера: значение, строение, изучение Презентация на тему Вода в природе 3 класс
Презентация на тему Вода в природе 3 класс  Презентация на тему Фалес Милетский
Презентация на тему Фалес Милетский Реки
Реки Блинчики-Мск. Проект
Блинчики-Мск. Проект Презентация на тему Чтобы путь был счастливым (3 класс)
Презентация на тему Чтобы путь был счастливым (3 класс) Развитие социальной психологии
Развитие социальной психологии проект ккт
проект ккт Установка коннектора компрессора на новых корейских компрессорах!
Установка коннектора компрессора на новых корейских компрессорах! Я РАДА ПРИВЕТСТВОВАТЬ ВАС НА УРОКЕ ФИЗИКИ
Я РАДА ПРИВЕТСТВОВАТЬ ВАС НА УРОКЕ ФИЗИКИ общая характеристика растений
общая характеристика растений Новогодний хороводНам очень веселоВозьмёмся за руки.. - презентация
Новогодний хороводНам очень веселоВозьмёмся за руки.. - презентация Биохимия почек и мочеобразования
Биохимия почек и мочеобразования Сертификация систем качества
Сертификация систем качества Презентация на тему Экологические факторы. Антропогенное воздействие на экосистемы
Презентация на тему Экологические факторы. Антропогенное воздействие на экосистемы Птичья азбука
Птичья азбука