Учебный курс Введение в параллельные алгоритмы

Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Ц Е Л Ь
О С Н О В Н А Я
Расположить в порядке
неубывания
N элементов массива чисел,
используя p процессоров
Москва, 2009 г.
из 29

Объём оперативной памяти одного процессорного узла достаточен для одновременного размещения в ней всех элементов массива
Объём оперативной памяти одного процессорного узла мал для одновременного размещения в ней всех элементов массива
Две задачи сортировки массива чисел
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.
из 29

Части массива хранятся на нескольких процессорах
Каждая часть массива должна быть упорядочена
На процессорах с большими номерами должны быть размещены элементы массива с большими значениями
Правильно
Ошибка
Ошибка
Задача B
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.
из 29

Будем рассматривать только процесс упорядочивания элементов:
Перед началом сортировки на каждом из процессоров уже есть часть элементов массива
После окончания сортировки на каждом из процессоров должно остаться столько элементов, сколько их было в начале (но, это уже могут быть другие элементы, расположенные ранее на других процессорах)
Задача B
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.
из 29

Упорядочивание фрагментов массива на каждом из процессоров
Перераспределение элементов массива между процессорами с сохранением упорядоченности массива на каждом отдельном процессоре
Этапы сортировки
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.
из 29

?
Стратегия перераспределения данных между процессорами
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.
из 29

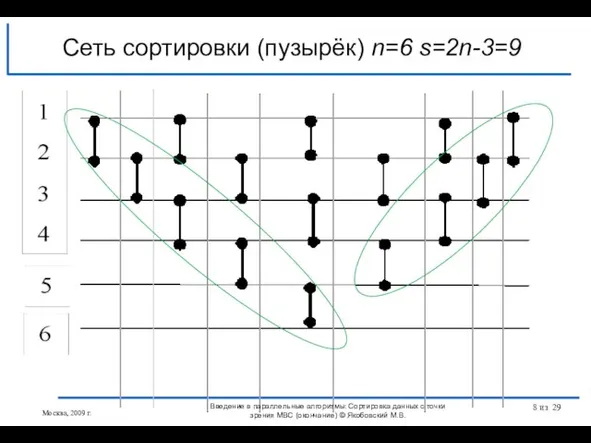
Сеть сортировки (пузырёк) n=6 s=2n-3=9
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

Сеть сортировки четно-нечетные перестановки n=6 s=n=6
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

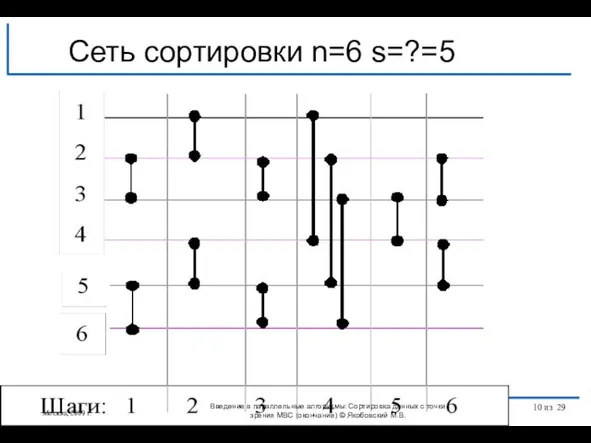
Сеть сортировки n=6 s=?=5
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

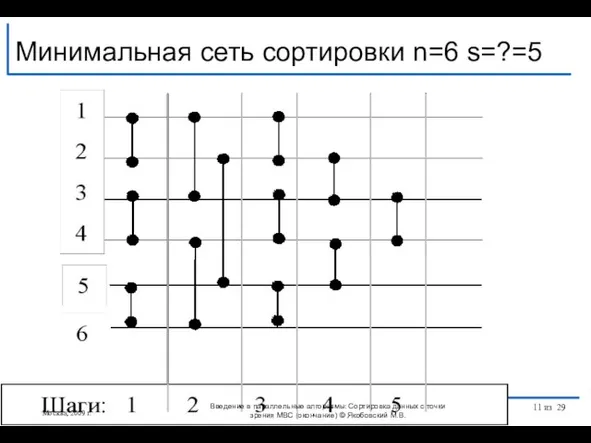
Минимальная сеть сортировки n=6 s=?=5
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

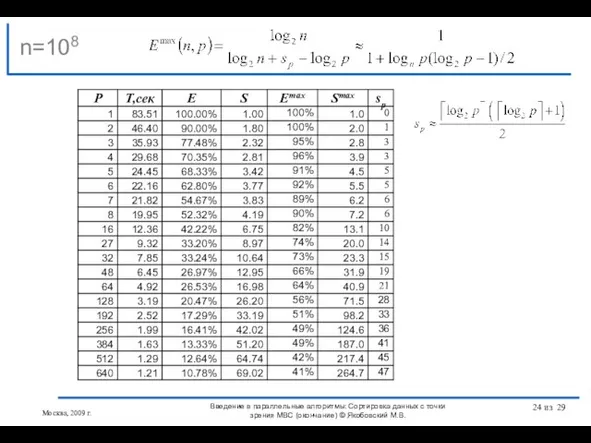
Минимальные сети сортировки
[Дональд Э.Кнут]
n=6 s=5
n=10 s=7
n=9 s=8
n=12 s=8
n=16 s=9

Объединение двух упорядоченных массивов размера m и n:
и
.
a) Если m=0 или n=0, то сеть пуста
b) m=n=1, то нужен один компаратор.
с) Если mn>1, то
сольём нечетные элементы последовательностей
и
, и получим
Сольём четные элементы последовательностей
и
, и получим
Применим операции сравнения перестановки к элементам
(w1,v2), (w2,v3), (w3,v4), …
И получим отсортированный массив
Четно-нечетное слияние Бэтчера
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

Доказать правильность можно на основе принципа нулей и единиц:
Если сеть с n входами сортирует в порядке неубывания все 2n последовательности из 0 и 1, то она будет сортировать в том же порядке любую последовательность n чисел.
Правильность сети
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

Сортировка 8ми элементов
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

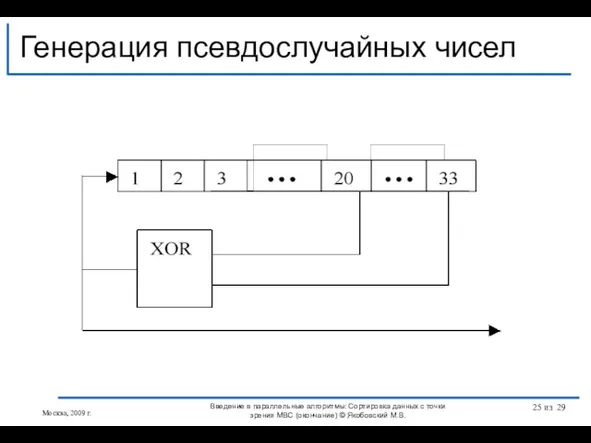
Обменная сортировка со слиянием
[Бэтчер]

Сортировка блоков – ОДИНАКОВОГО РАЗМЕРА
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

Сравнение алгоритмов сортировки
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.

Слияние упорядоченных фрагментов
// объединить два упорядоченных массива a,b
for(ia=0,ib=0,k=0;k
{
if(ia>=n1) c[k]=b[ib++];
else
if(ib>=n2) c[k]=a[ia++];
else
if(a[ia]
else c[k]=b[ib++];
}
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.
из 29

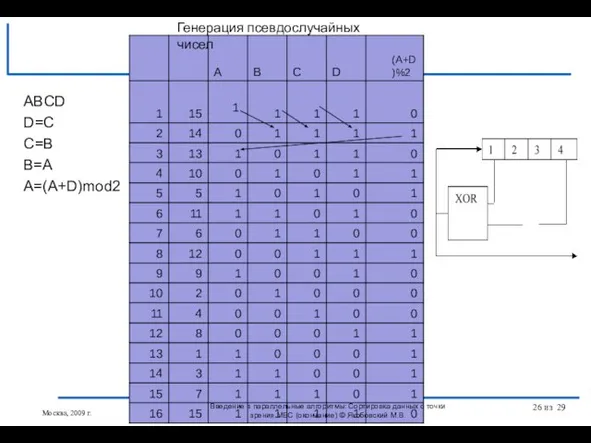
for(ia=0,ib=0,k=0;k
{
if(ia>=n1) c[k]=b[ib++];
else
if(ib>=n2) c[k]=a[ia++];
else
if(a[ia]
else c[k]=b[ib++];
}
// n – число элементов в каждом из массивов a,b
Слияние упорядоченных фрагментов
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.
rank1, a[n]
rank2, b[n]
из 29

Join(int *a, int *b, int *c, int n,rank1,rank2)
{
if(rank==rank1)
for(ia=0,ib=0,k=0;k
{
if(a[ia]
else c[k++]=b[ib++];
}
else
for(ia=n-1,ib=n-1,k=n-1;k>=0;)
{
if(a[ia]>b[ib]) c[k--]=a[ia--];
else c[k--]=b[ib--];
}
}
Слияние упорядоченных фрагментов
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.
rank1
rank2
из 29

// взаимодействие процессоров rank и rankC
int *a,*b,*c,*tmp;
ASend(a,n,rankC);
ARecv(b,n,rankC);
ASync();
Join(a,b,c,n,min(rank,rankC),max(rank,rankC));
tmp=a;
a=c;
c=tmp;
Реализация компаратора слияния
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

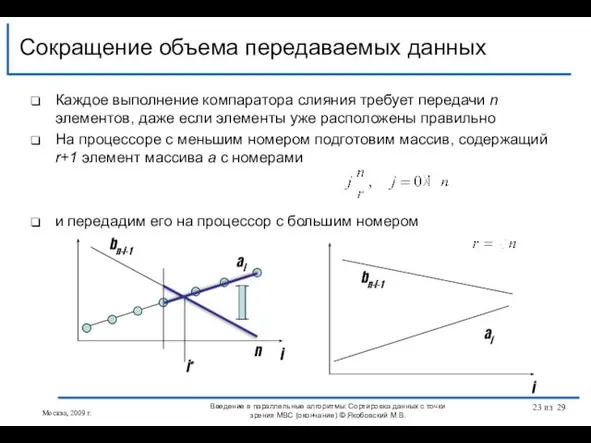
Каждое выполнение компаратора слияния требует передачи n элементов, даже если элементы уже расположены правильно
На процессоре с меньшим номером подготовим массив, содержащий r+1 элемент массива a с номерами
и передадим его на процессор с большим номером
Сокращение объема передаваемых данных
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
i
ai
bn-i-1
i
ai
bn-i-1
i*
n
из 29

n=108
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

Генерация псевдослучайных чисел
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

ABCD
D=C
C=B
B=A
A=(A+D)mod2
Генерация псевдослучайных чисел
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29

Рассмотрен ряд, основанных на сетях методов параллельной сортировки массивов
Рассмотрен вопрос оптимизации выполнения слияния на компараторе слияния
Рассмотрен вопрос сокращения числа шагов и объема передаваемых данных
Заключение
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
Москва, 2009 г.
из 29

Дональд Э.Кнут. Искусство программирования, т.3. Сортировка и поиск 2-е изд.: Пер. с английского – М.: Издательский дом «Вильямс», 2001.
Седжвик Роберт. Фундаментальные алгоритмы на С++. Анализ/Структуры данных/Сортировка/Поиск: Пер. с англ./Роберт Седжвик. - СПб.: ООО "ДиаСофтЮП", 2002.-688с.
Якобовский М.В. Параллельные алгоритмы сортировки больших объемов данных. Москва, 2008, http://lira.imamod.ru/FondProgramm/Sort/ParallelSort.pdf
Список литературы
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (окончание) © Якобовский М.В.
из 29