Удивительный мир земных звезд

Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел
Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел

Мир наш исполнен симметрии. С древнейших времен с ней связаны наши представления о красоте. Наверное, этим объясняется непреходящий интерес человека к удивительным символам симметрии, привлекавшим внимание множества выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши.
Симметрия

Виды правильных многогранников
Многогранник - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер — вершинами многогранника.
Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней.
Выпуклый многогранник называется правильным, если все его грани — правильные одинаковые многоугольники и все многогранные углы при вершинах равны.

Теорема Эйлера
Вершины + Грани - Рёбра = 2.
Многогранник Вершины Грани Рёбра Оси симметрии Плоскости
симметрии
Тетраэдр 4 4 6 3 6
Куб 8 6 12 9 9
Октаэдр 6 8 12 9 7
Додекаэдр 20 12 30 15 15
Икосаэдр 12 20 30 15 15

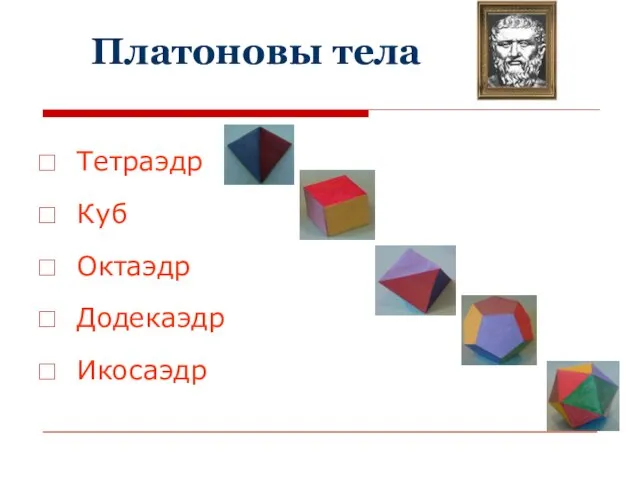
Платоновы тела
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр

Архимедовы тела

Кубок Кеплера
Вокруг сферы Меркурия описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.

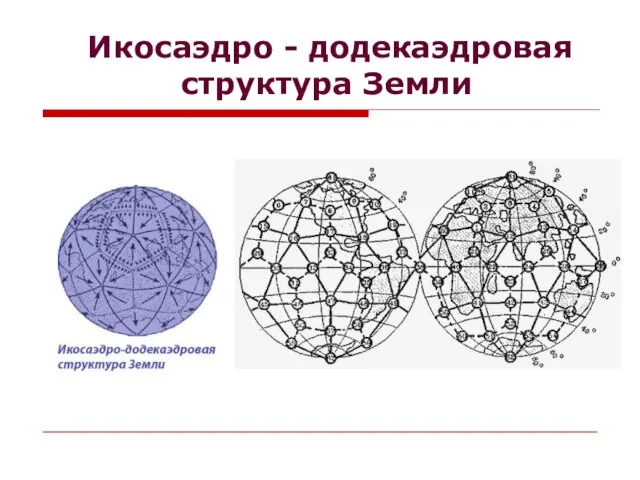
Икосаэдро - додекаэдровая структура Земли

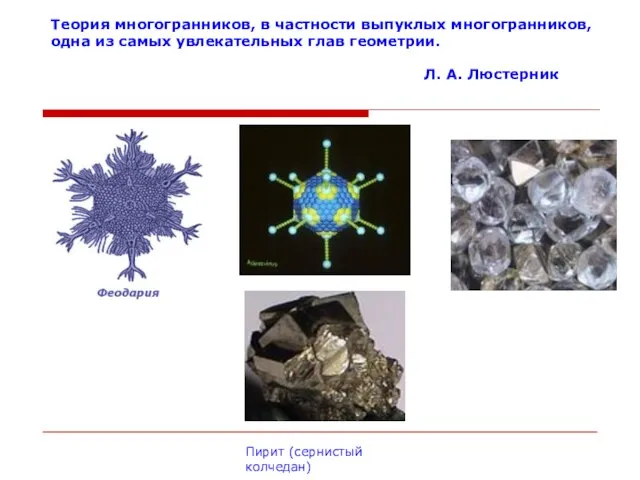
Теория многогранников, в частности выпуклых многогранников,
одна из самых увлекательных глав геометрии. Л. А. Люстерник
Пирит (сернистый колчедан)

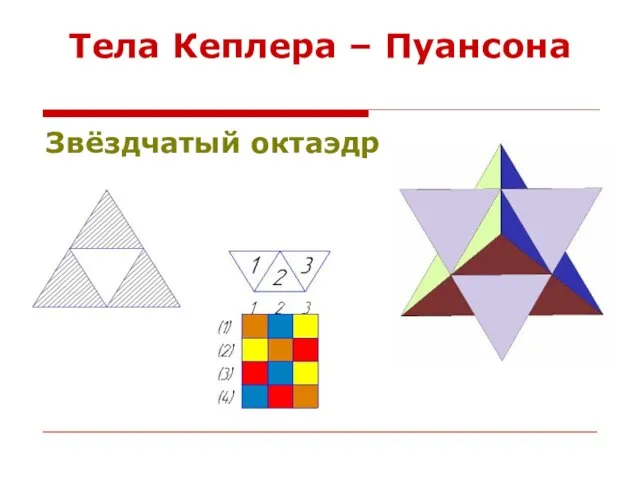
Тела Кеплера – Пуансона
Звёздчатый октаэдр

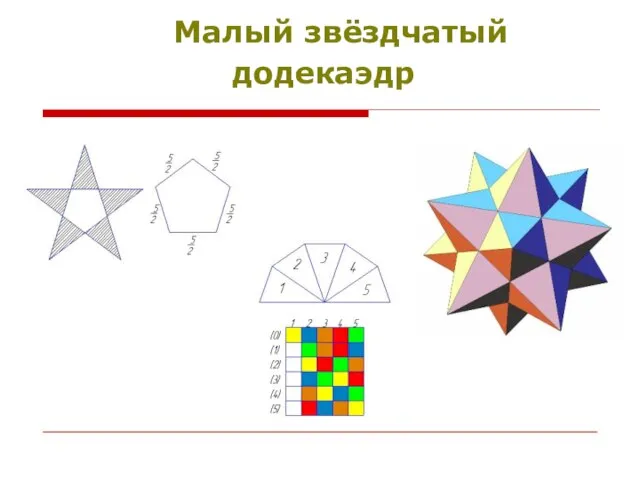
Малый звёздчатый додекаэдр

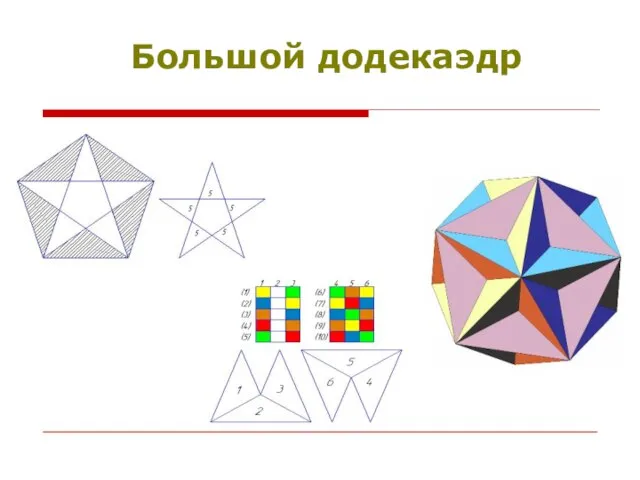
Большой додекаэдр

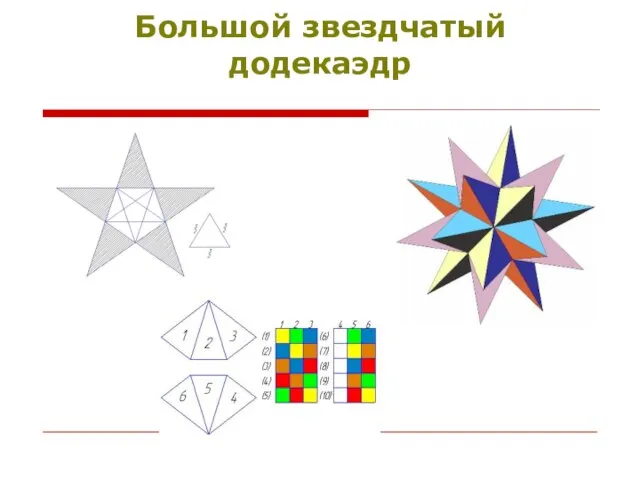
Большой звездчатый додекаэдр

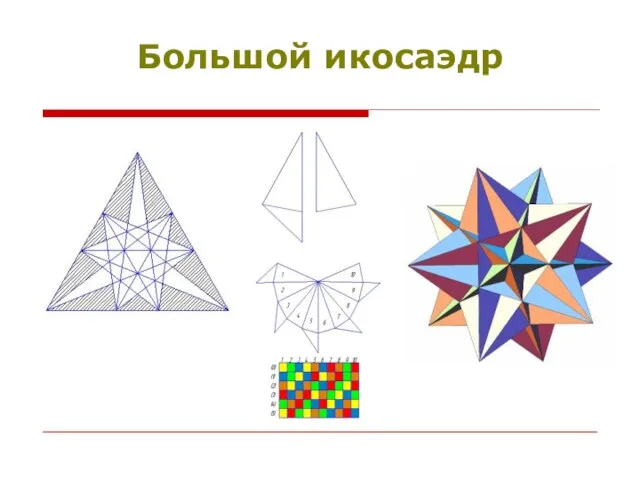
Большой икосаэдр