Содержание
- 2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
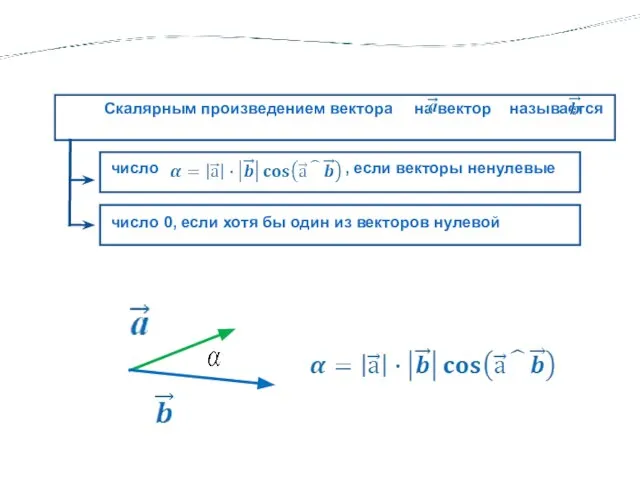
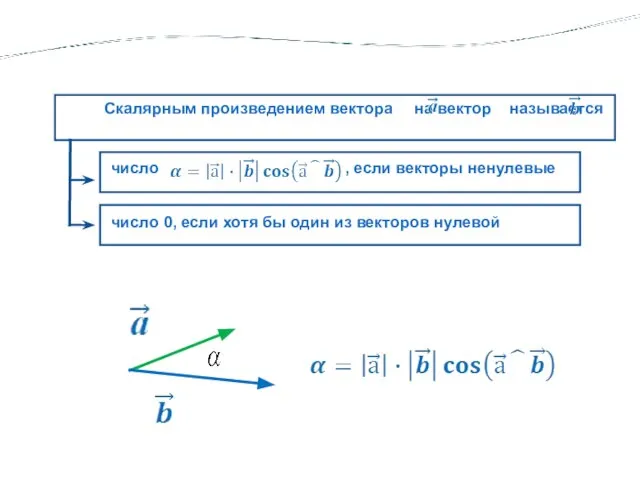
- 3. число , если векторы ненулевые Скалярным произведением вектора на вектор называется число 0, если хотя бы
- 4. число , если векторы ненулевые Скалярным произведением вектора на вектор называется число 0, если хотя бы
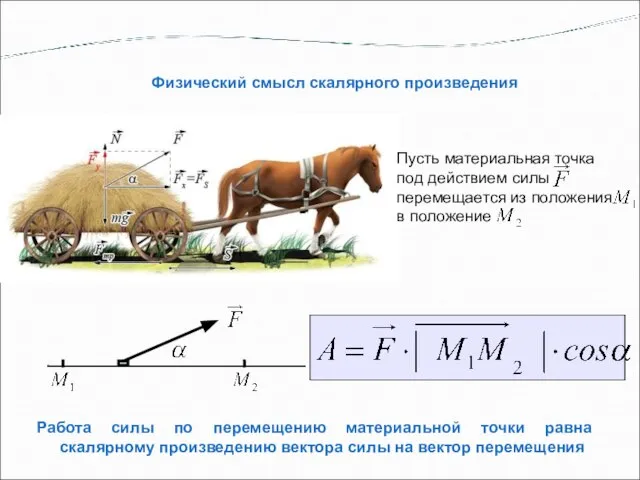
- 5. Пусть материальная точка под действием силы перемещается из положения в положение Физический смысл скалярного произведения Работа
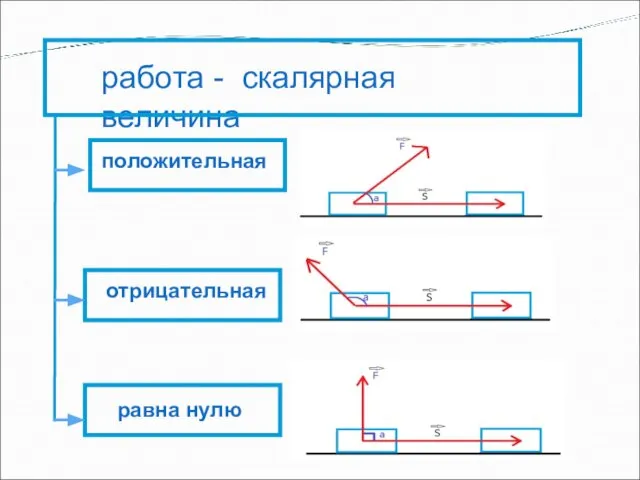
- 6. работа - скалярная величина положительная отрицательная равна нулю
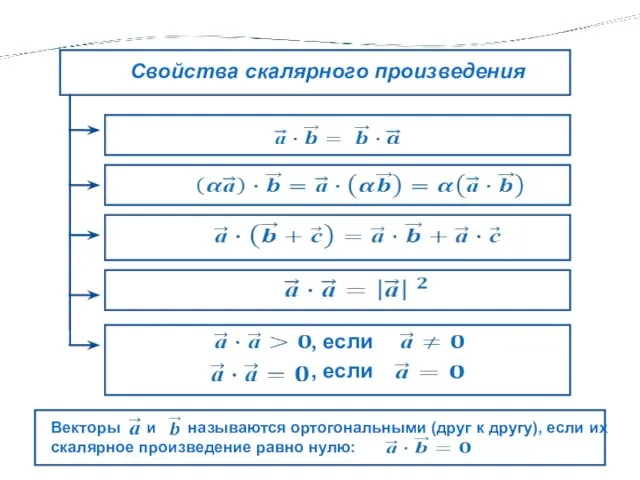
- 7. Свойства скалярного произведения векторов , если , если Векторы и называются ортогональными (друг к другу), если
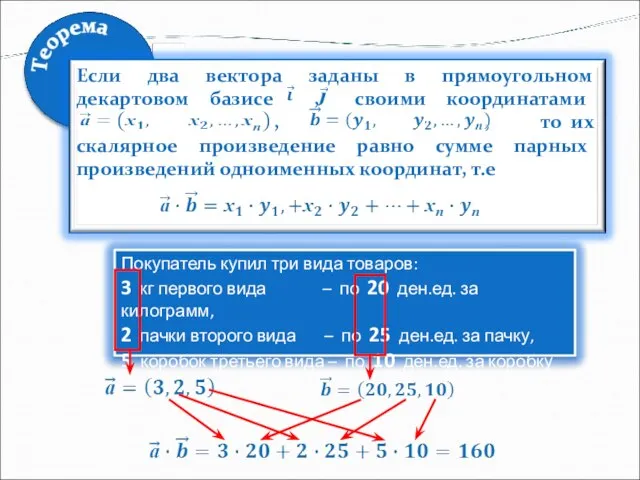
- 8. Согласно определению скалярного произведения
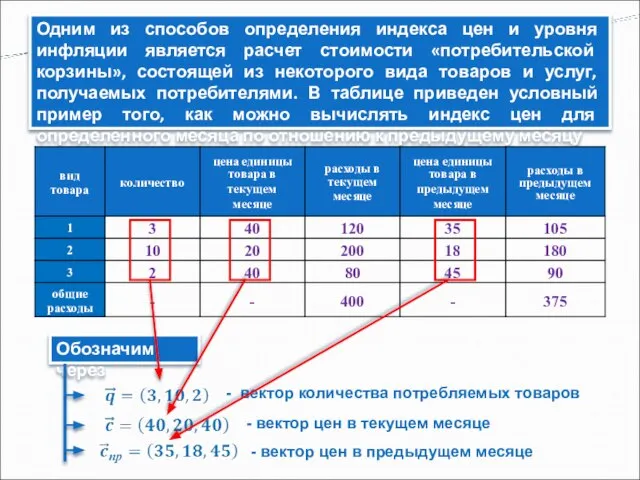
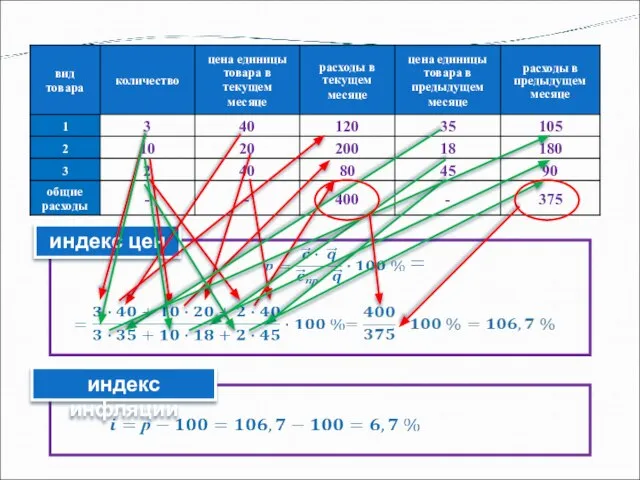
- 10. Одним из способов определения индекса цен и уровня инфляции является расчет стоимости «потребительской корзины», состоящей из
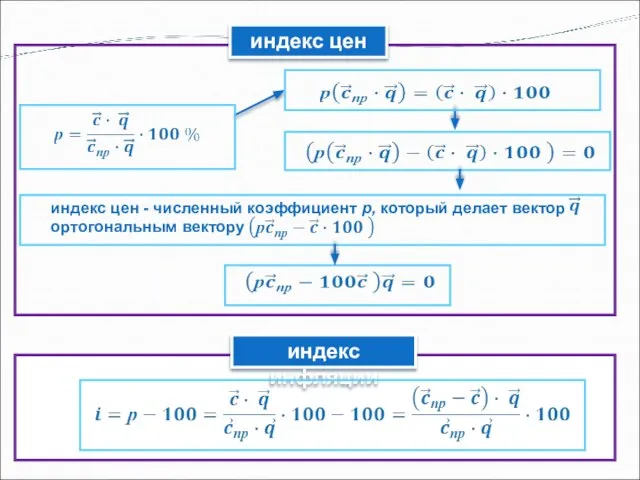
- 11. индекс цен индекс цен - численный коэффициент р, который делает вектор ортогональным вектору индекс инфляции
- 12. индекс цен индекс инфляции .
- 13. Дан вектор ………………………………………. своими координатами. Вычислить длину данного вектора. Даны два ненулевых вектора своими координатами и
- 14. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее заданным свойствам (рассматриваемым как аксиомы), называется
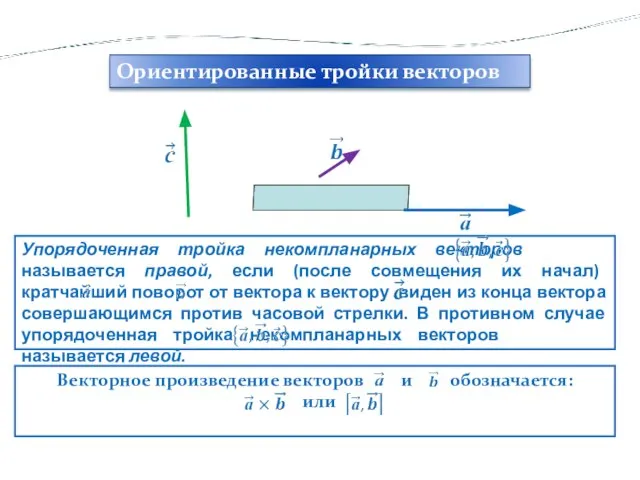
- 15. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
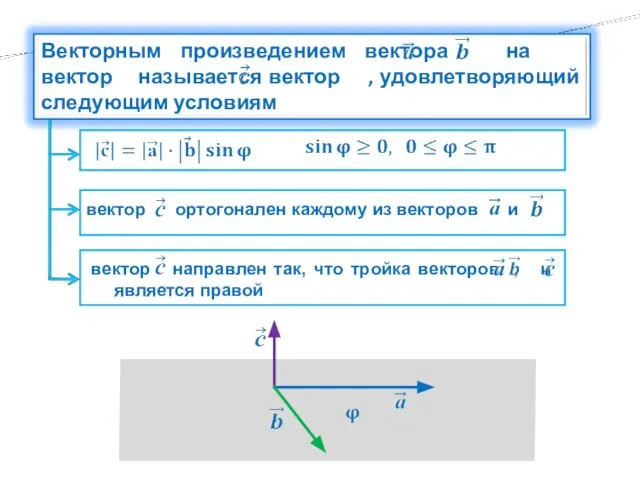
- 16. называется вектор вектор ортогонален каждому из векторов и вектор направлен так, что тройка векторов , и
- 17. Упорядоченная тройка некомпланарных векторов ………. называется правой, если (после совмещения их начал) кратчайший поворот от вектора
- 18. свойства векторного произведения векторов модуль векторного произведения ……. равен площади S параллелограмма, построенного на приведённых к
- 20. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
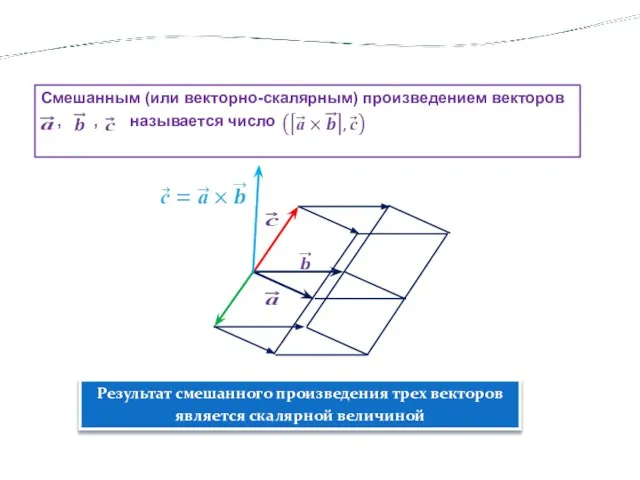
- 21. Результат смешанного произведения трех векторов является скалярной величиной Смешанным (или векторно-скалярным) произведением векторов …,……,……называется число
- 23. Скачать презентацию








 Презентация на тему Презентация Теорема Виета
Презентация на тему Презентация Теорема Виета ЛИПИДВЫСВОБОЖДАЮЩАЯ СПОСОБНОСТЬ ЛЕЙКОЦИТОВ ПРИ СТАБИЛЬНОЙ СТЕНОКАРДИИ С РАЗЛИЧНОЙ СТЕПЕНЬЮ ТЯЖЕСТИ СЕРДЕЧНОЙ НЕДОСТАТОЧНОСТИ.
ЛИПИДВЫСВОБОЖДАЮЩАЯ СПОСОБНОСТЬ ЛЕЙКОЦИТОВ ПРИ СТАБИЛЬНОЙ СТЕНОКАРДИИ С РАЗЛИЧНОЙ СТЕПЕНЬЮ ТЯЖЕСТИ СЕРДЕЧНОЙ НЕДОСТАТОЧНОСТИ. Вводный инструктаж по технике безопасности на уроках физической культуры
Вводный инструктаж по технике безопасности на уроках физической культуры Independent Phonographic Alliance (IPA)
Independent Phonographic Alliance (IPA) Презентація_Математика_Число 3
Презентація_Математика_Число 3 Основные нормативные акты по вопросам обороны и безопасности
Основные нормативные акты по вопросам обороны и безопасности Этимологический словарь
Этимологический словарь Православное учение о человеке
Православное учение о человеке Уникальные объекты природы в России и Калининградской области
Уникальные объекты природы в России и Калининградской области ТЕОРИЯ литературы
ТЕОРИЯ литературы Межэтнические конфликты в Китае
Межэтнические конфликты в Китае Реставрации на ордени, медали, значки и нагръдни знаци
Реставрации на ордени, медали, значки и нагръдни знаци Профессиональная Ассоциация, как механизм повышения качества деятельности специалистов в сфере защиты прав детства А.М. Марова П
Профессиональная Ассоциация, как механизм повышения качества деятельности специалистов в сфере защиты прав детства А.М. Марова П Этикет. Игровая программа
Этикет. Игровая программа NewBeautyBox
NewBeautyBox Самостоятельная работа
Самостоятельная работа Клуб по месту жительства Ёжики
Клуб по месту жительства Ёжики Развитее жизни на земле
Развитее жизни на земле Канальный уровень в ЛВС
Канальный уровень в ЛВС Клоун из соленого теста
Клоун из соленого теста ДЕТСКИЕ ПОЧЕМУЧКИ.
ДЕТСКИЕ ПОЧЕМУЧКИ. Презентация на тему Древняя и современная природа земли
Презентация на тему Древняя и современная природа земли  Mery Christmas
Mery Christmas  Методика для экспресс анализа структур при многих критериях (оперативного анализа структур)
Методика для экспресс анализа структур при многих критериях (оперативного анализа структур) ладок ты мой
ладок ты мой Эквалайзеры для ручного, оперативного изменения АЧХ
Эквалайзеры для ручного, оперативного изменения АЧХ Маркетингово-ориентированное управление
Маркетингово-ориентированное управление Презентация на тему Определение производной от функции
Презентация на тему Определение производной от функции