Содержание
- 2. Множество есть многое, мыслимое нами как единое Георг Кантор
- 3. Способы задания множеств: 1.Описание. Описание, включает основной, характеристический признак множества 2.Список Например, множество учеников нашего класса
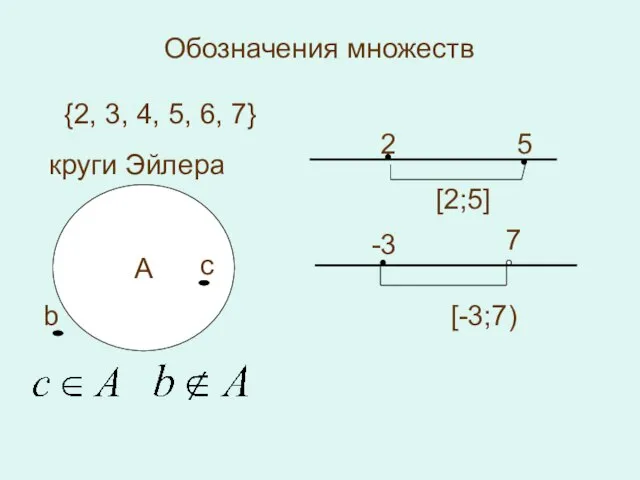
- 4. А Обозначения множеств {2, 3, 4, 5, 6, 7} круги Эйлера с b 2 5 [2;5]
- 5. Примеры Множество синиц Множество воробьев
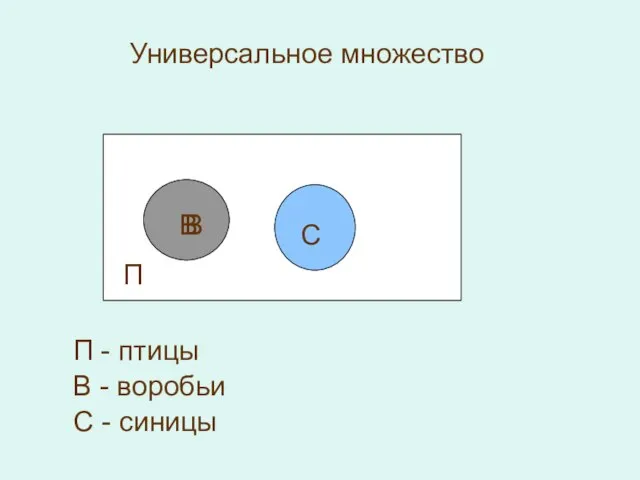
- 6. Универсальное множество П В В С П - птицы В - воробьи С - синицы
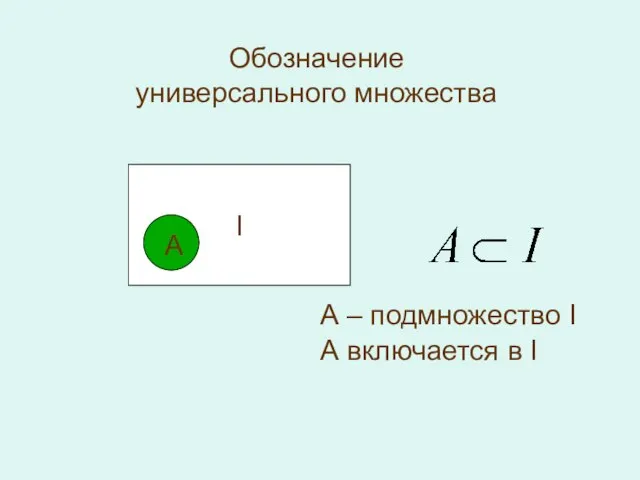
- 7. Обозначение универсального множества I А А – подмножество I А включается в I
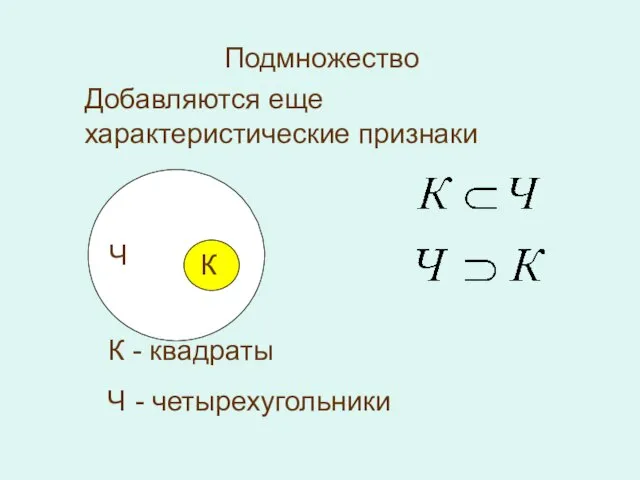
- 8. Подмножество К Ч К - квадраты Ч - четырехугольники Добавляются еще характеристические признаки
- 9. Пустое множество Множество называется пустым, если в нем нет ни одного элемента
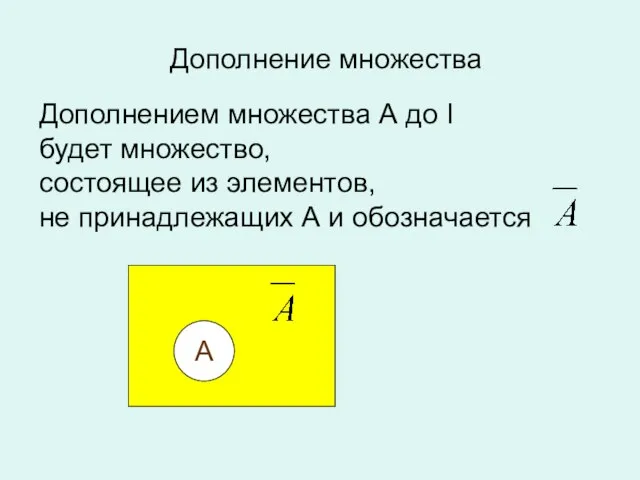
- 10. Дополнение множества Дополнением множества А до I будет множество, состоящее из элементов, не принадлежащих А и
- 11. Урок 5 Действия с множествами
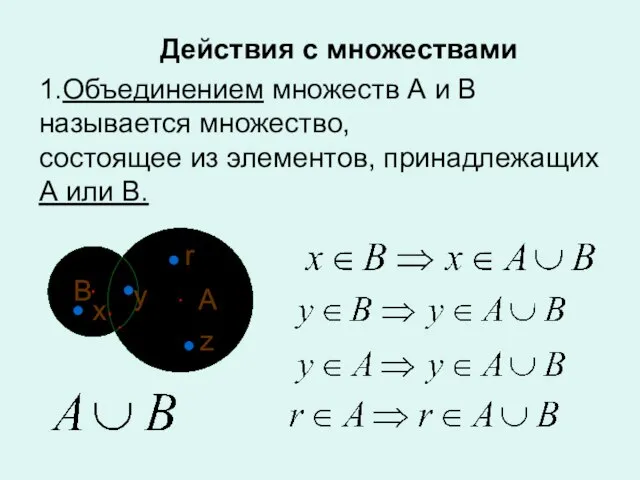
- 12. Действия с множествами 1.Объединением множеств А и В называется множество, состоящее из элементов, принадлежащих А или
- 13. А={2;3;4;5;7} B={3;5;8;9} 1 4 5 7
- 14. 2. Пересечением множеств А и В называется множество, состоящее из элементов, принадлежащих А и В. A
- 15. А={2;3;4;5;7} B={3;5;8;9} 1 4 5 7
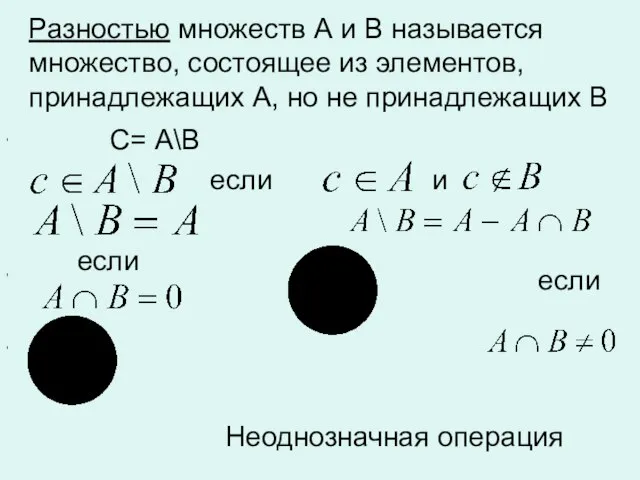
- 17. , , , Разностью множеств А и В называется множество, состоящее из элементов, принадлежащих А, но
- 19. Скачать презентацию







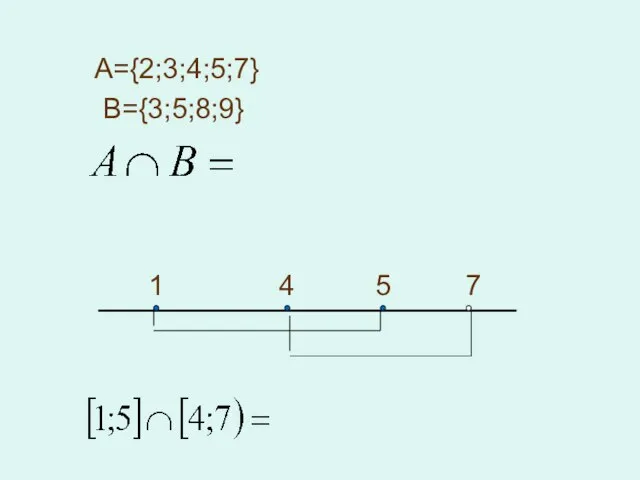

 Этапы принятия решения
Этапы принятия решения Викторина Iч 2022 26.10
Викторина Iч 2022 26.10 Режущий инструмент лущильных станков
Режущий инструмент лущильных станков Презентация на тему На пути к индустриальной эре
Презентация на тему На пути к индустриальной эре  Транспортно-пересадочные узлы в рамках реализации комплексного инвестиционного проекта «Реконструкция и развитиеМалого кольца
Транспортно-пересадочные узлы в рамках реализации комплексного инвестиционного проекта «Реконструкция и развитиеМалого кольца Презентация (2)
Презентация (2) Петрович. Моя корзина
Петрович. Моя корзина Бер өн менән генә айырылған һүҙҙәр уйла
Бер өн менән генә айырылған һүҙҙәр уйла Источники и системы теплоснабжения
Источники и системы теплоснабжения Природный стиль. Драма
Природный стиль. Драма Уильям Шекспир
Уильям Шекспир Как усовершенствовать учебную деятельность
Как усовершенствовать учебную деятельность Декларация о правах ребенка
Декларация о правах ребенка Ташкент – столица Узбекистана
Ташкент – столица Узбекистана История становления СПО НИКА УралГУФК
История становления СПО НИКА УралГУФК Месяц безопасности
Месяц безопасности Презентация на тему Родная природа в стихотворениях русских поэтов 19 века
Презентация на тему Родная природа в стихотворениях русских поэтов 19 века Рельеф Южной Америки
Рельеф Южной Америки Yarema Zyelyk
Yarema Zyelyk Еко-туризм в селі Дмитрівка, Одеській області
Еко-туризм в селі Дмитрівка, Одеській області Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений
Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений Карьера
Карьера Акционерный капитал
Акционерный капитал Стилистическая эволюция в творчестве Матиса Готхарта-Нитхарта
Стилистическая эволюция в творчестве Матиса Готхарта-Нитхарта ПРЕДВАРИТЕЛЬНЫЕ ИТОГИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ ОМСКОЙ ОБЛАСТИ В 2010 ГОДУ
ПРЕДВАРИТЕЛЬНЫЕ ИТОГИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ ОМСКОЙ ОБЛАСТИ В 2010 ГОДУ Самообразование педагога
Самообразование педагога Олимпийские игры. Где и когда проходили первые Олимпийские игры
Олимпийские игры. Где и когда проходили первые Олимпийские игры Таёжная область Северного Урала
Таёжная область Северного Урала