Урок презентация на тему ЗАДАЧИ НА РАЗРЕЗАНИЕ

Основная цель:
познакомить учащихся с задачами на разрезание;
развитие пространственного представления и логического мышления, интуиции и смекалки.

Основное содержание
Историческая справка.
Разновидности задач на
разрезание.
Геометрические софизмы и занимательные задачи.

Задачи на разрезание и перекраивание возникли в глубокой древности:
VII – V вв. до н. э. в Индии в книге «Правила веревки»
II в. до н. э. в «Началах» Евклида
1832 – 1833 гг. теорема Больяи – Гервина (равновеликие многоугольники являются равносоставленными)
XX в. Генри Э. Дьюдени и Гарри Линдгрен – классики занимательной геометрии
ИСТОРИЧЕСКАЯ СПРАВКА

Разновидности
задач на разрезание
Задачи, которые являются составляющими вывода формул площадей параллелограмма, треугольника, трапеции
Задачи на разрезание греческого креста
Задачи на перекраивание двух фигур в равновеликую им третью фигуру

ОПРЕДЕЛЕНИЯ
Равновеликие фигуры – плоские фигуры, имеющие равные площади
Равносоставленные фигуры – это фигуры, которые можно разрезать на одинаковое число соответственно равных частей

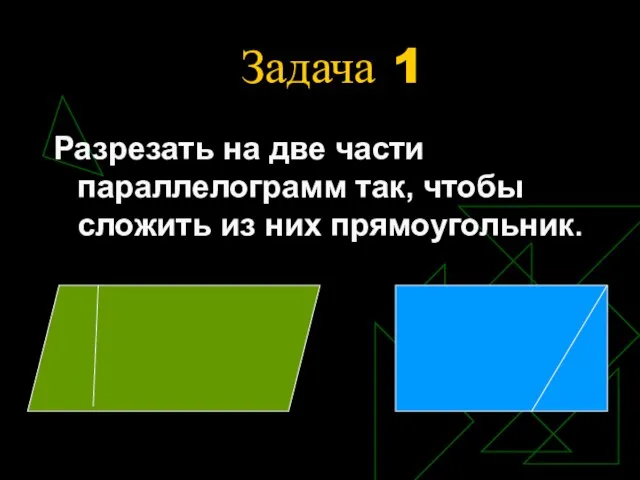
Задача 1
Разрезать на две части параллелограмм так, чтобы сложить из них прямоугольник.

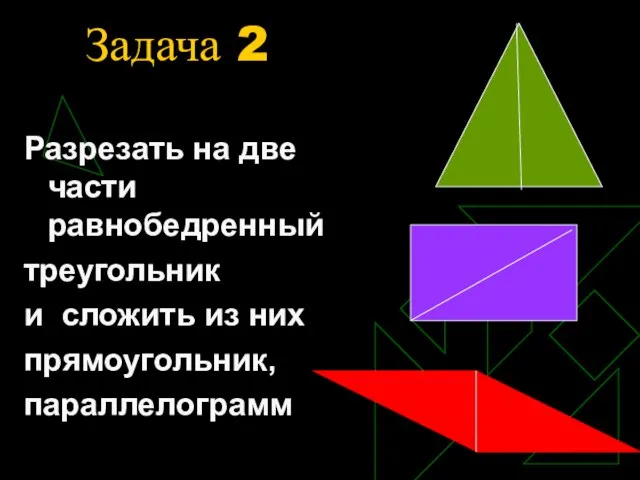
Задача 2
Разрезать на две части равнобедренный
треугольник
и сложить из них
прямоугольник,
параллелограмм

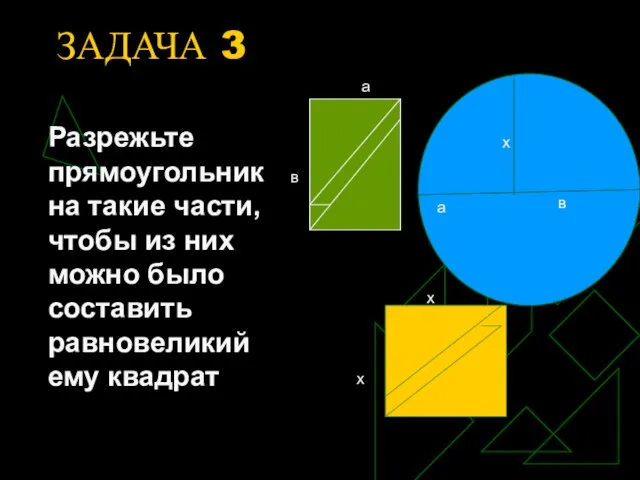
ЗАДАЧА 3
Разрежьте прямоугольник на такие части, чтобы из них можно было составить равновеликий ему квадрат
а
в
а
в
х
х
х

Задачи на разрезание греческого креста
Греческий крест – это многоугольник, составленный из пяти равных квадратов

ЗАДАЧА 4
Разрежьте греческий крест на такие части, чтобы из них можно было составить равновеликий ему квадрат.

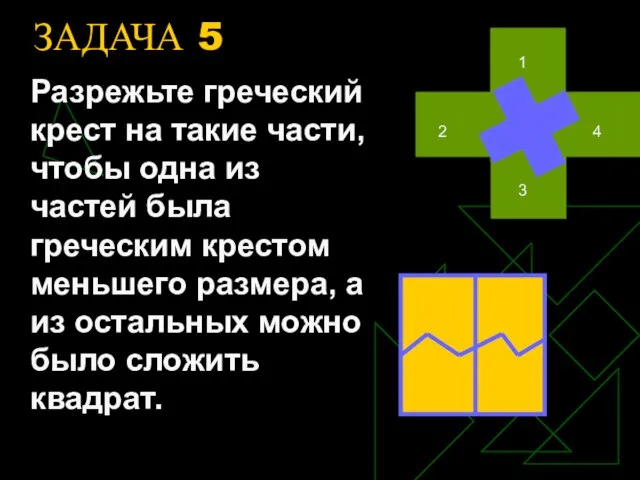
ЗАДАЧА 5
Разрежьте греческий крест на такие части, чтобы одна из частей была греческим крестом меньшего размера, а из остальных можно было сложить квадрат.

Геометрические софизмы и занимательные задачи.
Софизм - рассуждение, обосновывающее заведомую нелепость, абсурд или парадоксальное утверждение.
Геометрический софизм – ошибочный чертеж или кажущиеся «очевидности».

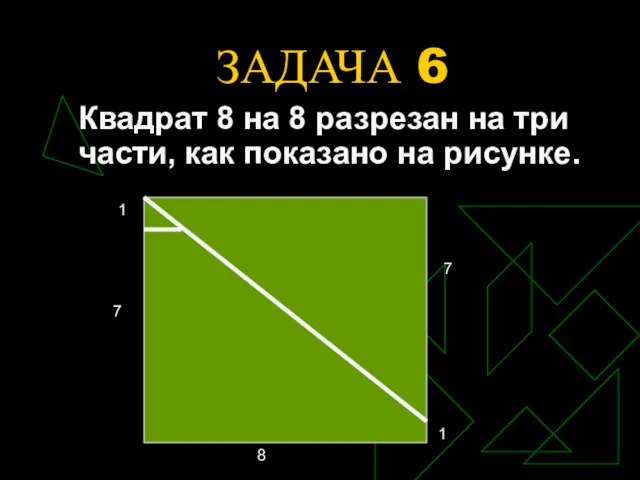
ЗАДАЧА 6
Квадрат 8 на 8 разрезан на три части, как показано на рисунке.

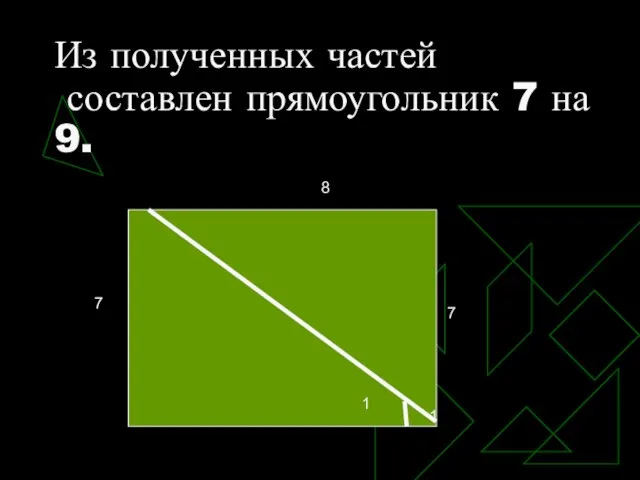
Из полученных частей составлен прямоугольник 7 на 9.

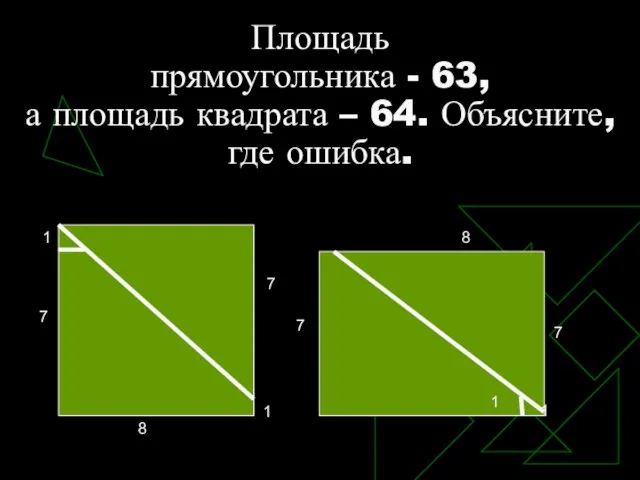
Площадь
прямоугольника - 63,
а площадь квадрата – 64. Объясните, где ошибка.

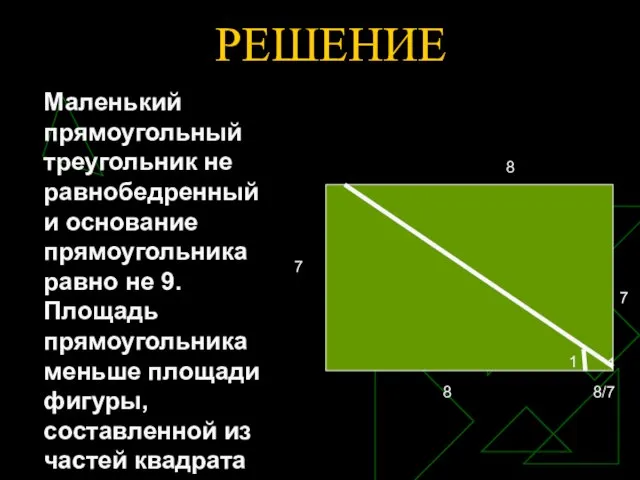
РЕШЕНИЕ
Маленький прямоугольный треугольник не равнобедренный и основание прямоугольника равно не 9. Площадь прямоугольника меньше площади фигуры, составленной из частей квадрата