Усечённая пирамида

ПИРАМИДА
ПОНЯТИЕ ПОНЯТИЕ УСЕЧЕННОЙ ПИРАМИДЫ
ПРАВИЛЬНАЯ УСЕЧЁННАЯ ПИРАМИДА
ПЛОЩАДЬ ПОВЕРХНОСТИ ПЛОЩАДЬ ПОВЕРХНОСТИ УСЕЧЁННОЙ ПИРАМИДЫ
ЗАДАЧИ
СОДЕРЖАНИЕ

ПИРАМИДА
ПОНЯТИЕ УСЕЧЕННОЙ ПИРАМИДЫ
Плоскость параллельная основанию пирамиды, разбивает её на два многогранника. Один из них является пирамидой, а другой называется усечённой пирамидой.
Усеченная пирамида – это часть полной пирамиды, заключенная между её основанием и секущей плоскостью, параллельной основанию данной пирамиды
СОДЕРЖАНИЕ

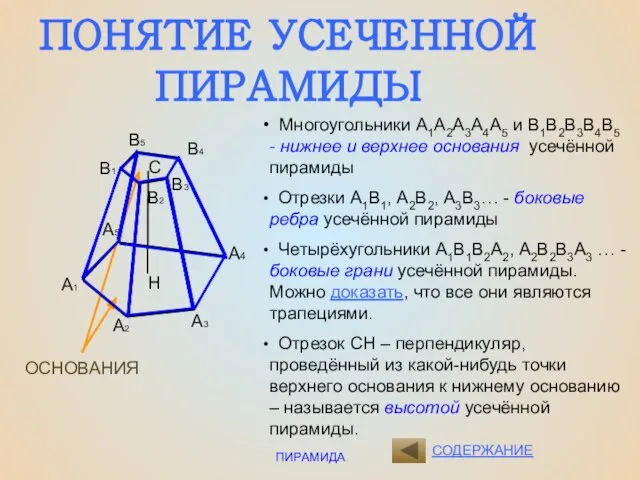
ПИРАМИДА
СОДЕРЖАНИЕ
ПОНЯТИЕ УСЕЧЕННОЙ ПИРАМИДЫ
ОСНОВАНИЯ
С
Н
Многоугольники А1А2А3А4А5 и В1В2В3В4В5 - нижнее и верхнее основания усечённой пирамиды
Отрезки А1В1, А2В2, А3В3… - боковые ребра усечённой пирамиды
Четырёхугольники А1В1В2А2, А2В2В3А3 … - боковые грани усечённой пирамиды. Можно доказать, что все они являются трапециями.
Отрезок СН – перпендикуляр, проведённый из какой-нибудь точки верхнего основания к нижнему основанию – называется высотой усечённой пирамиды.

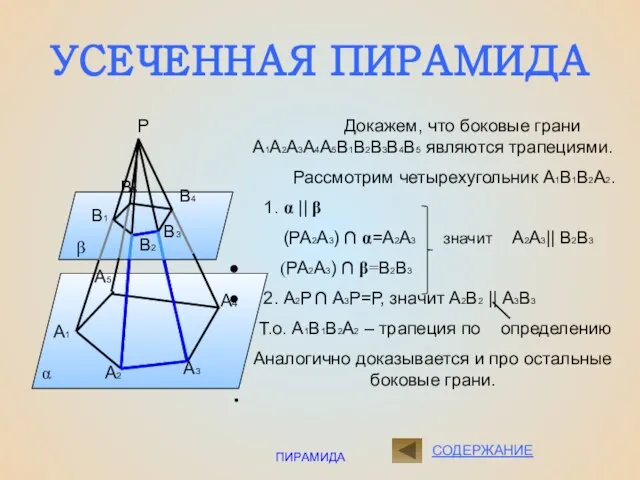
ПИРАМИДА
УСЕЧЕННАЯ ПИРАМИДА
α
β
Р
Докажем, что боковые грани А1А2А3А4А5В1В2В3В4В5 являются трапециями.
Рассмотрим четырехугольник А1В1В2А2.
1. α || β
(РА2А3) ∩ α=А2А3 значит А2А3|| В2В3
(РА2А3) ∩ β=В2В3
2. А2Р ∩ А3Р=Р, значит А2В2 || А3В3
Т.о. А1В1В2А2 – трапеция по определению
Аналогично доказывается и про остальные боковые грани.
СОДЕРЖАНИЕ

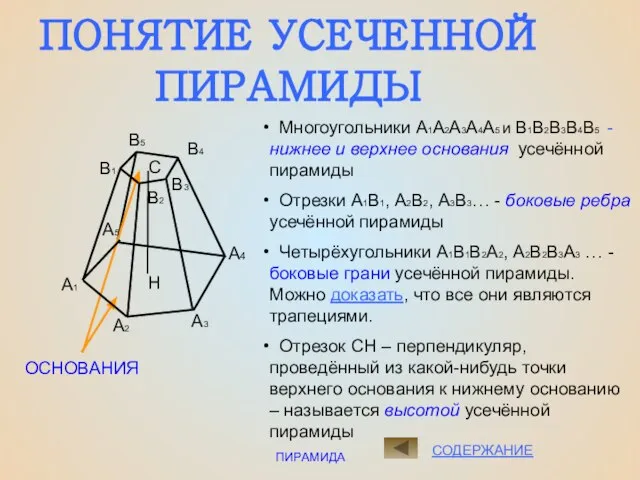
ПИРАМИДА
СОДЕРЖАНИЕ
ПОНЯТИЕ УСЕЧЕННОЙ ПИРАМИДЫ
ОСНОВАНИЯ
С
Н
Многоугольники А1А2А3А4А5 и В1В2В3В4В5 - нижнее и верхнее основания усечённой пирамиды
Отрезки А1В1, А2В2, А3В3… - боковые ребра усечённой пирамиды
Четырёхугольники А1В1В2А2, А2В2В3А3 … - боковые грани усечённой пирамиды. Можно доказать, что все они являются трапециями.
Отрезок СН – перпендикуляр, проведённый из какой-нибудь точки верхнего основания к нижнему основанию – называется высотой усечённой пирамиды

ПИРАМИДА
ПРАВИЛЬНАЯ УСЕЧЕННАЯ ПИРАМИДА
СОДЕРЖАНИЕ
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.
Основания - правильные многоугольники .
Боковые грани – равные равнобедренные трапеции (?).
Высоты этих трапеций называются апофемами.

ПИРАМИДА
СОДЕРЖАНИЕ
ПРАВИЛЬНАЯ ПИРАМИДА
Пирамида называется правильной, если её основание – правильный многоугольник, если её основание – правильный многоугольник, а отрезок , соединяющий вершину с центром основания, является её высотой.
Все боковые рёбра правильной пирамиды равны, а грани являются равными равнобедренными треугольниками.
Высота боковой грани правильной пирамиды называется апофемой. Все апофемы правильной пирамиды равны друг другу.

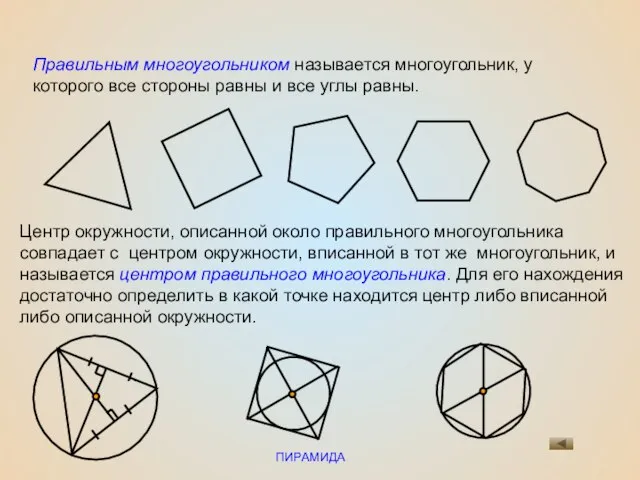
ПИРАМИДА
Правильным многоугольником называется многоугольник, у которого все стороны равны и все углы равны.
Центр окружности, описанной около правильного многоугольника совпадает с центром окружности, вписанной в тот же многоугольник, и называется центром правильного многоугольника. Для его нахождения достаточно определить в какой точке находится центр либо вписанной либо описанной окружности.

ПИРАМИДА
СОДЕРЖАНИЕ
УСЕЧЕННЫЕ ПИРАМИДЫ

ПИРАМИДА
СОДЕРЖАНИЕ
Площадью полной поверхности (Sполн) пирамиды называется сумма площадей всех её граней: основания и всех боковых граней.
Площадью боковой поверхности (Sбок) пирамиды называется сумма площадей её боковых граней.
Sполн =Sбок+Sосн
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему. Доказать.
ПЛОЩАДЬ ПОВЕРХНОСТИ УСЕЧЁННОЙ ПИРАМИДЫ
Sполн.усеч.=Sбок+Sверхн.осн.+Sнижн.осн.

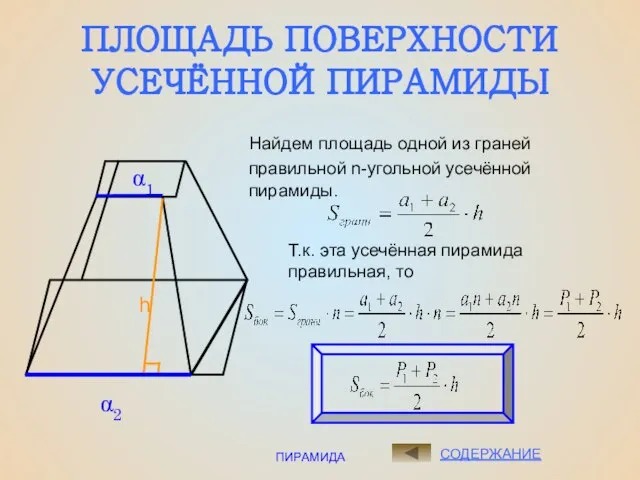
ПИРАМИДА
ПЛОЩАДЬ ПОВЕРХНОСТИ УСЕЧЁННОЙ ПИРАМИДЫ
СОДЕРЖАНИЕ
Найдем площадь одной из граней правильной n-угольной усечённой пирамиды.
α2
α1
h
Т.к. эта усечённая пирамида правильная, то

ПИРАМИДА
ЗАДАЧА 1
Найдите: 1. апофему пирамиды;
2. площадь полной поверхности.
СОДЕРЖАНИЕ
Стороны оснований правильной треугольной усеченной пирамиды равны 4 см и 2 см, а боковое ребро равно 2 см.

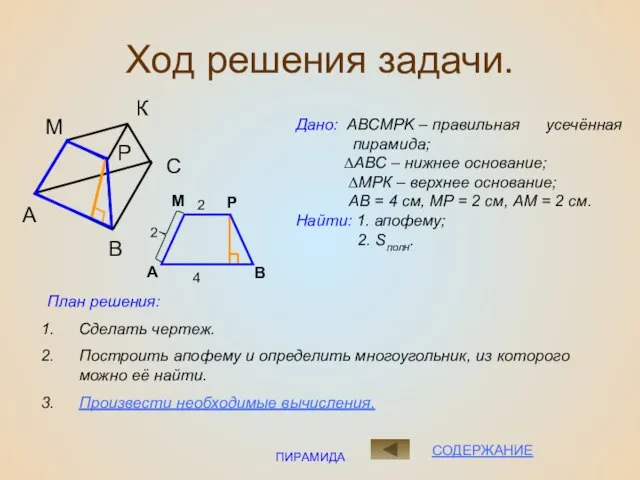
ПИРАМИДА
Ход решения задачи.
Дано: ABCMPK – правильная усечённая пирамида;
∆АВС – нижнее основание; ∆МРК – верхнее основание;
АВ = 4 см, МР = 2 см, АМ = 2 см.
Найти: 1. апофему;
2. Sполн.
План решения:
Сделать чертеж.
Построить апофему и определить многоугольник, из которого можно её найти.
Произвести необходимые вычисления.
СОДЕРЖАНИЕ
2
2
4

ПИРАМИДА
РЕШЕНИЕ
А
В
М
Р
2
2
Н
С
2
СОДЕРЖАНИЕ
АВ=АН+АС+СВ
СВ=АН АВ=2АН+МР
НС=МР
Т.о. 2АН=2, АН=1
∆АМН – прямоугольный, ∠АНМ=90°
АН= по теореме Пифагора.
4
Sполн=Sбок+Sверхн.осн.+Sнижн.осн.
т.к. в основании правильные треугольники

ПИРАМИДА
РЕШЕНИЕ
Ответ:
СОДЕРЖАНИЕ

ПИРАМИДА
ЗАДАЧА 2
Плоскость, параллельная плоскости основания правильной четырехугольной пирамиды, делит высоту пирамиды в отношении 1:2, считая от вершины пирамиды. Апофема полученной усеченной пирамиды равна 4 см, а площадь её полной поверхности равна 186 см2.
Найдите высоту усечённой пирамиды.
СОДЕРЖАНИЕ