Содержание
- 2. Арифметика зачастую не в силах собственными средствами доказать правильность некоторых из её утверждений. Ей приходится в
- 4. Мгновенное умножение Попробуйте решить вычисление 9882. Если будите выполнять обычным вычислением, это займёт много времени. И
- 5. 9882 = 988х988 = (988+12)х(988 – 12)+122 = = 1000х976+144 = 976 144. 632=(63+3)х(63-3)+32=3969; 182=20х16+22=324 и
- 6. Для быстрого возведения в квадрат чисел, оканчивающихся на 5, очень удобен следующий способ: 352; 3х4=12 Ответ:1225
- 8. Цифры 1, 5 и 6 Вероятно, все заметили, что от перемножения ряда чисел, оканчивающихся единицей или
- 10. Числа 25 и 76 Имеются и двузначные числа, обладающие тем же свойством, как и числа 1,
- 12. Делимость на 11. Алгебра весьма облегчает отыскание признаков, по которым можно заранее, не выполняя деления, установить,
- 13. Проверим эту теорию, например, число 87 635 064: 8+6+5+6=25, 7+3+0+4=14, 25-14=11. Значит, данное число делится на
- 14. Существует и другой признак делимости на 11, удобный для не очень длинных чисел. Он состоит в
- 16. Делимость на 19 Число делится без остатка на 19 тогда и только тогда, когда число его
- 17. 4704588|1 +2 --------------------- 47045|90 +18 -------------------- 4706|3 +6 -------------------- 471|2 +4 --------------------- 47|5 +10 --------------------- 5|7
- 19. Скачать презентацию



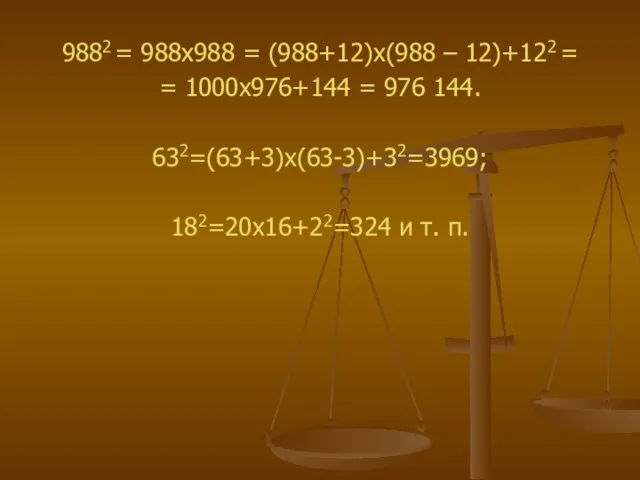












 Виды театральных кукол
Виды театральных кукол 1 урок Основы строительного черчения
1 урок Основы строительного черчения Mult_1_081
Mult_1_081 ПРЕДЛОЖЕНИЯ ПО РАЗВИТИЮ КОНЦЕПЦИИ НАЦИОНАЛЬНОЙ ПЛАТЕЖНОЙ СИСТЕМЫ
ПРЕДЛОЖЕНИЯ ПО РАЗВИТИЮ КОНЦЕПЦИИ НАЦИОНАЛЬНОЙ ПЛАТЕЖНОЙ СИСТЕМЫ Практика в агентстве видеорекламы
Практика в агентстве видеорекламы Презентация на тему Деепричастие как часть речи
Презентация на тему Деепричастие как часть речи Наложение повязок
Наложение повязок Понятие о пряже и прядении, ткани и ткачестве
Понятие о пряже и прядении, ткани и ткачестве The Baikal: is it a lake or a sea?
The Baikal: is it a lake or a sea? Зайцеобразные
Зайцеобразные Проблемный подход в обучении географии
Проблемный подход в обучении географии Организационная культура. Стили руководства
Организационная культура. Стили руководства Дизайн-проект С-Пб МЧС ЦПС
Дизайн-проект С-Пб МЧС ЦПС Обобщающий урок в 3 классе
Обобщающий урок в 3 классе Автопробег Восточный экспресс
Автопробег Восточный экспресс Система работы с текстом на уроках русского языка как средство формирования коммуникативной компетентности
Система работы с текстом на уроках русского языка как средство формирования коммуникативной компетентности Нравственное воспитание: патриот, гражданин
Нравственное воспитание: патриот, гражданин Египет. Арабская Республика Египет
Египет. Арабская Республика Египет Региональная физико-географическая характеристика Внутренней и Внешней Монголии
Региональная физико-географическая характеристика Внутренней и Внешней Монголии Of course, studying is not easy
Of course, studying is not easy НЕТ терроризму.
НЕТ терроризму. История искусства Франции рубежа XVIII — XIX вв
История искусства Франции рубежа XVIII — XIX вв Медиабезопасность
Медиабезопасность Організація обслуговування за місцем роботи
Організація обслуговування за місцем роботи Домашняя работа для 2 курса
Домашняя работа для 2 курса Коммерческие банки
Коммерческие банки Декоративно-пркладное искусство России
Декоративно-пркладное искусство России Легковые автомобили
Легковые автомобили