Содержание
- 2. Примеры из физики
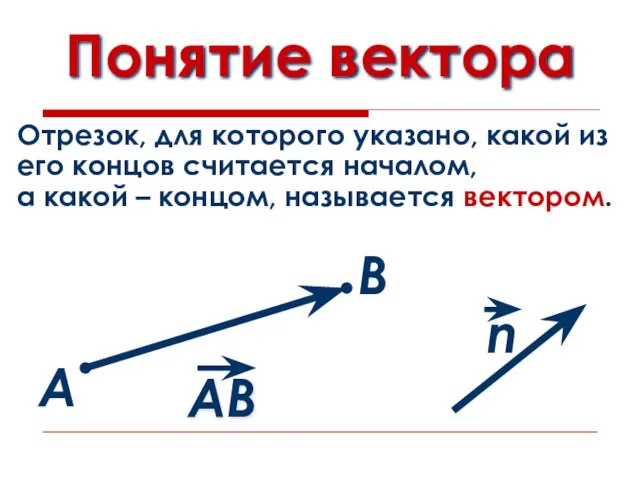
- 3. Понятие вектора А В Отрезок, для которого указано, какой из его концов считается началом, а какой
- 4. Нулевой вектор Любая точка на плоскости может рассматриваться как вектор. М Такой вектор называется нулевым.
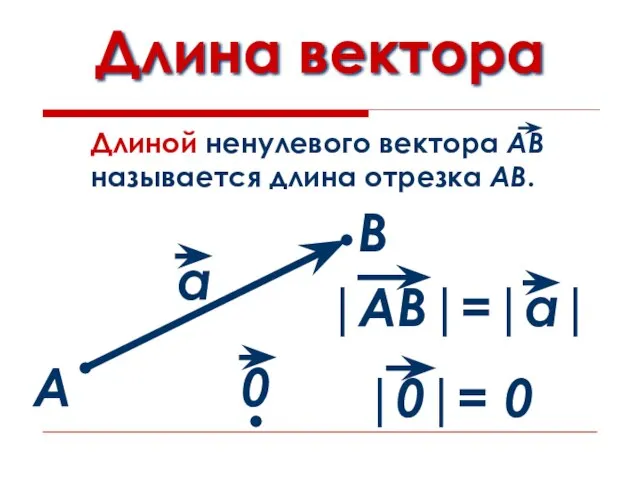
- 5. Длина вектора А В
- 6. Коллинеарность векторов Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных
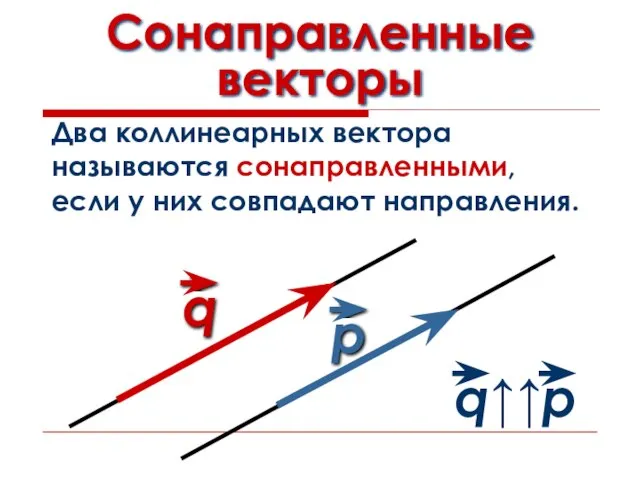
- 7. Сонаправленные векторы Два коллинеарных вектора называются сонаправленными, если у них совпадают направления.
- 8. Противоположно направленные векторы Два коллинеарных вектора называются противоположно направленными, если они не сонаправлены.
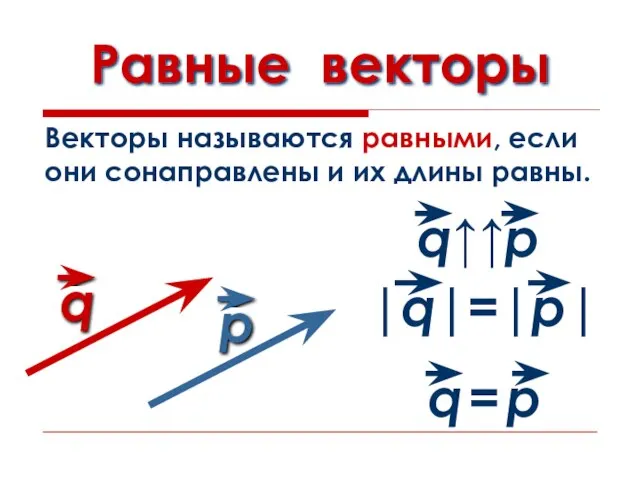
- 9. Равные векторы Векторы называются равными, если они сонаправлены и их длины равны.
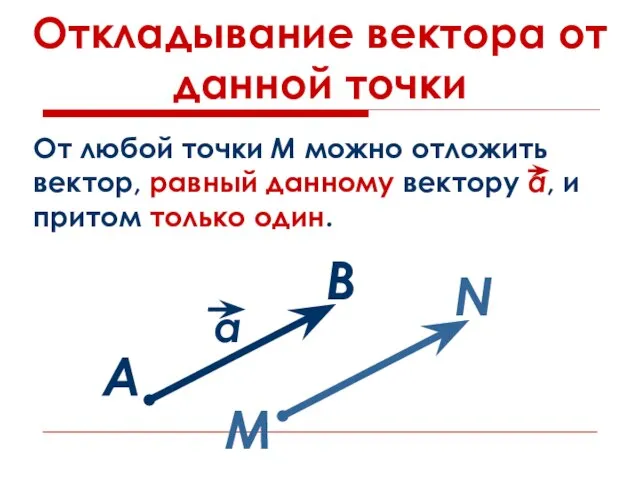
- 10. Откладывание вектора от данной точки А В М N
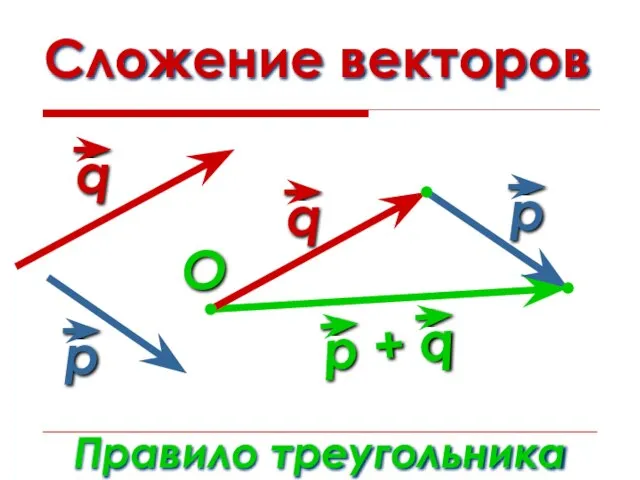
- 11. Сложение векторов Правило треугольника O
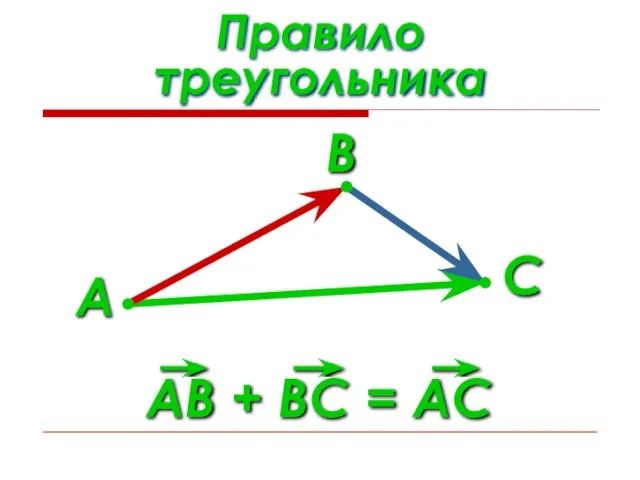
- 12. Правило треугольника А В С
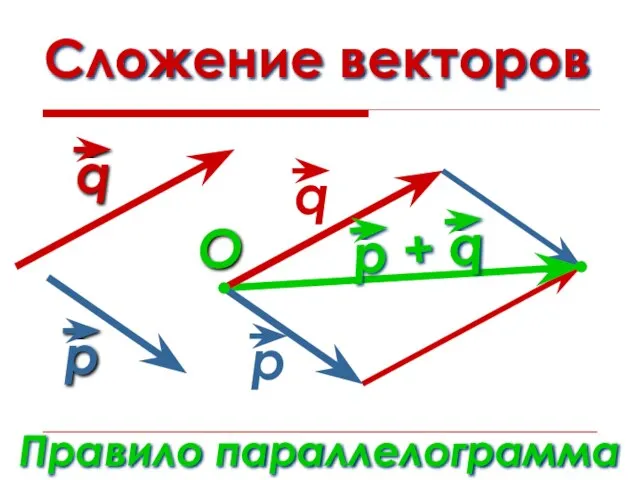
- 13. Сложение векторов Правило параллелограмма O
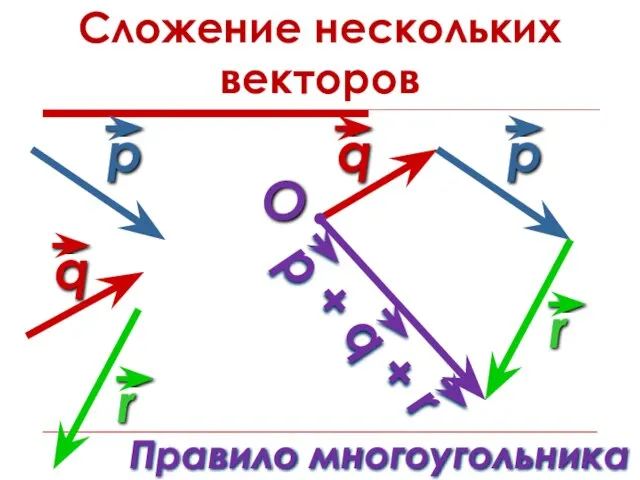
- 14. Сложение нескольких векторов O Правило многоугольника
- 15. Свойства сложения − переместительный закон − сочетательный закон − разность векторов
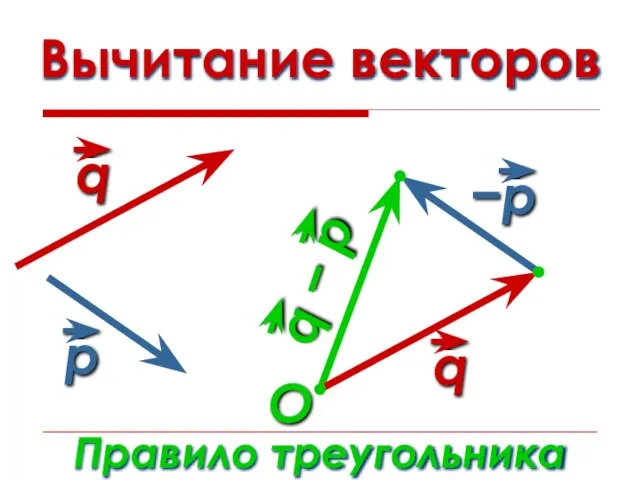
- 16. Вычитание векторов Правило треугольника O
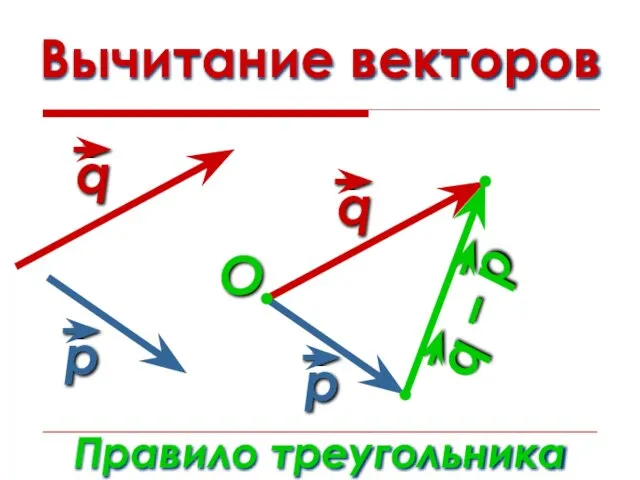
- 17. Вычитание векторов Правило треугольника O
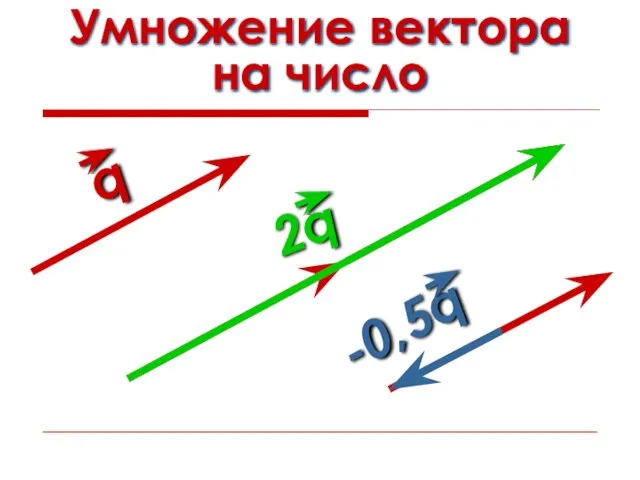
- 18. Умножение вектора на число
- 19. Свойства умножения − первый распределительный закон − сочетательный закон − второй распределительный закон
- 20. Применение векторов к решению задач
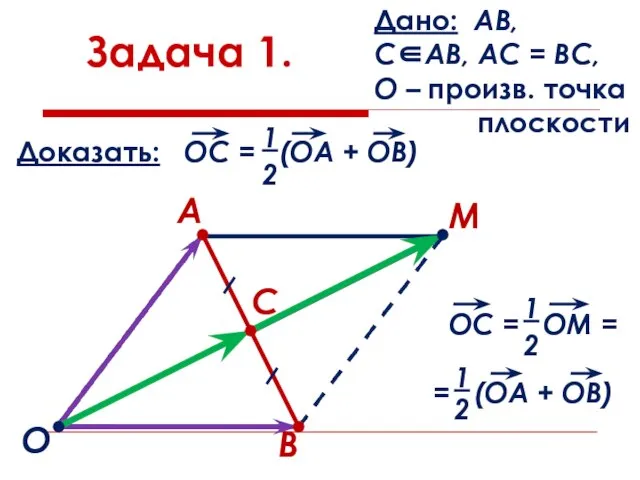
- 21. Задача 1. Дано: АВ, С∈АВ, АС = ВС, О – произв. точка плоскости О А В
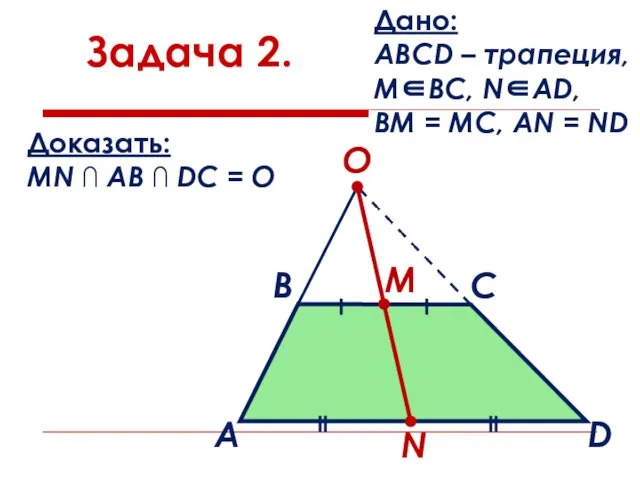
- 22. Задача 2. Дано: АВСD – трапеция, М∈ВС, N∈AD, BM = MC, AN = ND Доказать: MN
- 24. Скачать презентацию







 Мой друг – спорт. Верю – не верю
Мой друг – спорт. Верю – не верю Клаус Шваб Четвертая промышленная революция
Клаус Шваб Четвертая промышленная революция Потребности и расходы. Управление семейным бюджетом
Потребности и расходы. Управление семейным бюджетом Презентация на тему Музыкальные инструменты на Руси
Презентация на тему Музыкальные инструменты на Руси Презентация на тему Что общего у разных растений
Презентация на тему Что общего у разных растений  Права на чужие вещи
Права на чужие вещи  Привлекательная инвестиция. Производство электроэнергии и тепла в Вологодской области, Россия
Привлекательная инвестиция. Производство электроэнергии и тепла в Вологодской области, Россия Презентация на тему Сравнительное наблюдение за прорастанием семян
Презентация на тему Сравнительное наблюдение за прорастанием семян Так в чем же польза катания на коньках?
Так в чем же польза катания на коньках? Презентация на тему Магнитные свойства вещества
Презентация на тему Магнитные свойства вещества Organizatsia
Organizatsia ТЕМА №5
ТЕМА №5 Презентация на тему Внутреннее строение млекопитающих
Презентация на тему Внутреннее строение млекопитающих Past Continuos Tense
Past Continuos Tense Лес и его обитатели
Лес и его обитатели бух учет шамов
бух учет шамов Векторная графика
Векторная графика Растение в интерьере жилого дома
Растение в интерьере жилого дома Поморские небылицы
Поморские небылицы Презентация на тему Биогеоценоз и биоценоз
Презентация на тему Биогеоценоз и биоценоз Станция обнаружения целей (СОЦ). Блок череспериодной компенсации и индикатор кругового обзора. Эксплуатация ЧПК и ИКО
Станция обнаружения целей (СОЦ). Блок череспериодной компенсации и индикатор кругового обзора. Эксплуатация ЧПК и ИКО Монастыри России
Монастыри России Презентация на тему Бурундуки
Презентация на тему Бурундуки Презентация по технике безопасности
Презентация по технике безопасности Старинные занимательные математические задачи
Старинные занимательные математические задачи Воздействие на документ. Изменения свойств бумаги. Люминесценция. Воздействие на тонер
Воздействие на документ. Изменения свойств бумаги. Люминесценция. Воздействие на тонер Своя игра 2
Своя игра 2 вставь пропущенную букву
вставь пропущенную букву