Векторы в пространстве Геометрия-10

Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом.
На рисунках направление вектора обозначается стрелкой от начала к концу.
Если длина рассматриваемого отрезка равна нулю, то есть отрезок вырождается в точку, то эта точка тоже может рассматриваться как вектор.
Такой вектор называется нулевым и имеет произвольное направление.

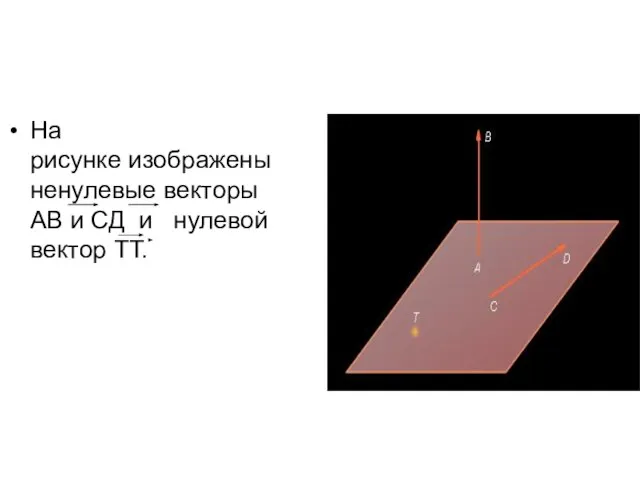
На рисунке изображены ненулевые векторы АВ и СД и нулевой вектор ТТ.

Длиной (модулем) ненулевого вектора
называется длина отрезка AB.
Она обозначается как |АВ|
Длина нулевого вектора равна нулю:| ТТ| =0

Два ненулевых вектора называются
коллинеарными,
если они лежат на одной прямой
или на параллельных прямых.
Поскольку нулевой вектор может иметь
произвольное направление,
то разумно считать его коллинеарным
любому ненулевому вектору.
А
В
С
Р
Т

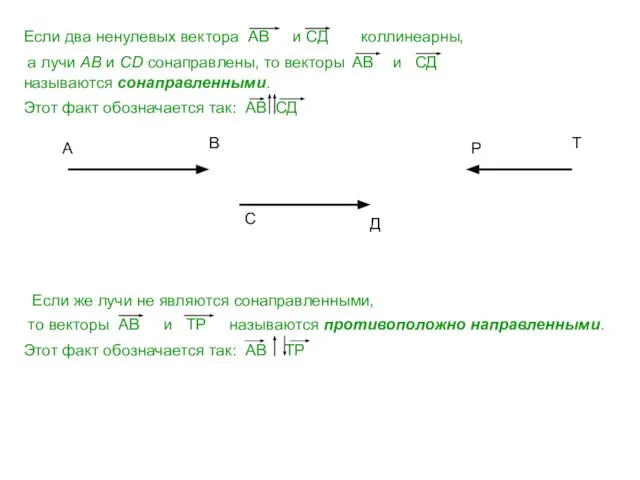
Если два ненулевых вектора АВ и СД коллинеарны,
а лучи AB и CD сонаправлены, то векторы АВ и СД
называются сонаправленными.
Этот факт обозначается так: АВ СД
Если же лучи не являются сонаправленными,
то векторы АВ и ТР называются противоположно направленными.
Этот факт обозначается так: АВ ТР
А
В
С
Д
Р
Т

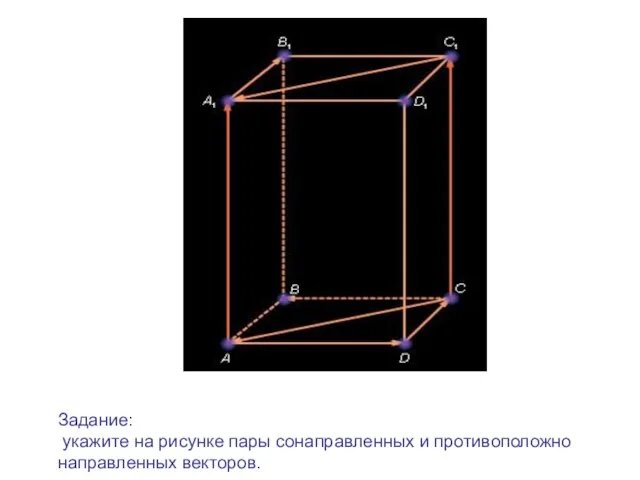
На рисунке 9.1.2
На рисунке 9.1.2
На рисунке 9.1.2
На рисунке 9.1.2
Задание:
укажите на рисунке пары сонаправленных и противоположно
направленных векторов.

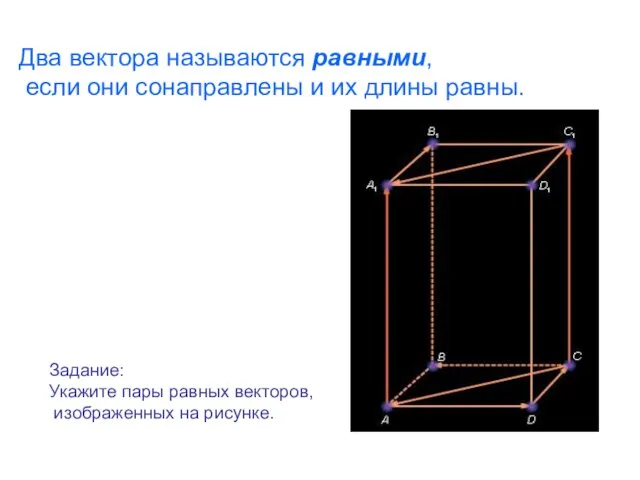
Два вектора называются равными,
если они сонаправлены и их длины равны.
Задание:
Укажите пары равных векторов,
изображенных на рисунке.

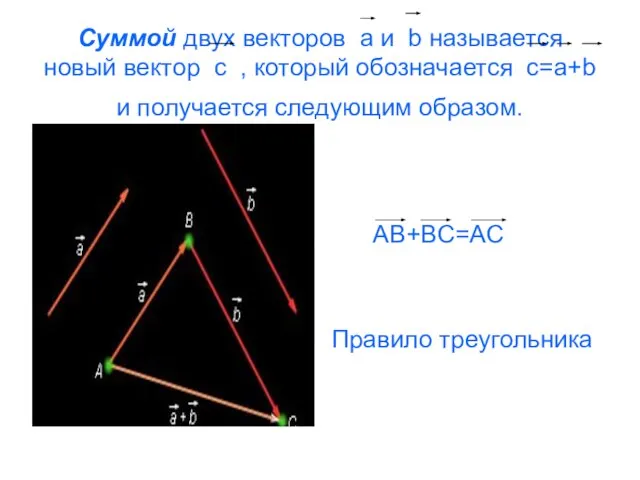
Суммой двух векторов a и b называется новый вектор c , который обозначается c=a+b и получается следующим образом.
AB+BC=AC
Правило треугольника

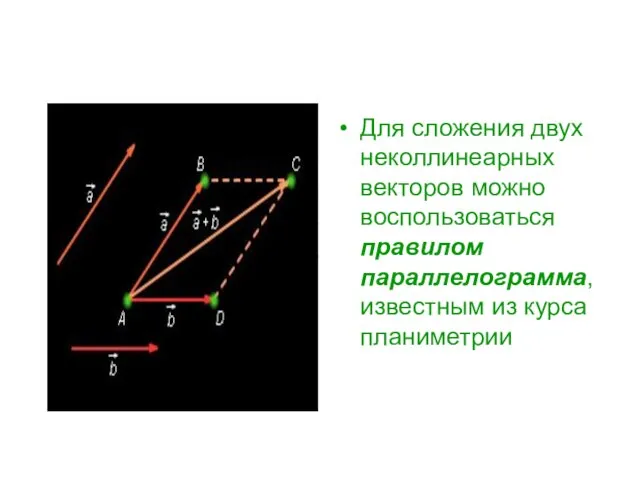
Для сложения двух неколлинеарных векторов можно воспользоваться правилом параллелограмма, известным из курса планиметрии

Законы сложения векторов

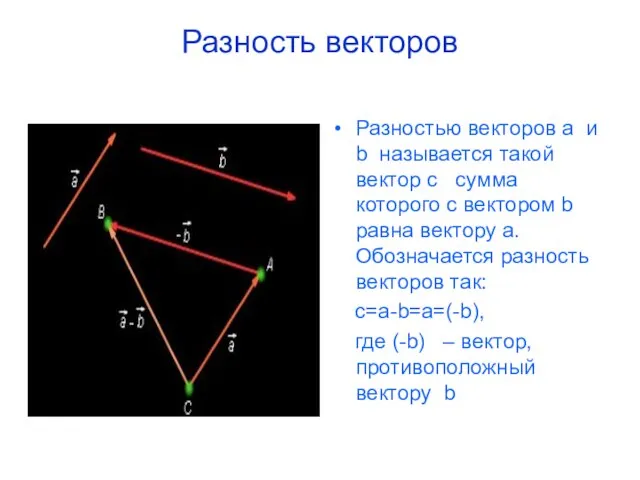
Разность векторов
Разностью векторов a и b называется такой вектор c сумма которого с вектором b равна вектору a. Обозначается разность векторов так:
c=a-b=a=(-b),
где (-b) – вектор, противоположный вектору b

Умножение вектора на число
Произведением ненулевого вектора a на число k называется вектор b длина которого равна |k| |a| причем при k > 0 векторы a и ka сонаправлены, а при k < 0 – противоположно направлены.
Произведением любого числа на нулевой вектор является нулевой вектор.
Из определения следует, что векторы a и ka коллинеарны. Кроме того, произведение любого вектора на число 0 есть нулевой вектор.