Содержание
- 2. Цели: Знать понятие вероятности события; виды событий; формулу для вычисления вероятности. Уметь вычислять в простейших случаях
- 3. СЛУЧАЙНОЕ СОБЫТИЕ Определение: Примеры: Выпадение орла при подбрасывании монеты. Выпадение шестёрки при бросании игральной кости. Выигрыш
- 4. ДОСТОВЕРНОЕ СОБЫТИЕ Определение: Примеры: Извлечение из урны , где лежат белые шары, белого шара. Выпадение одного
- 5. Невозможное событие Определение: Примеры: Выпадение числа 7 при бросании игральной кости. Извлечение черного шара из урны
- 6. При одном бросании игральной кости могут появиться числа 1,2,3,4,5,6. Каждое из этих событий случайно, т.к. оно
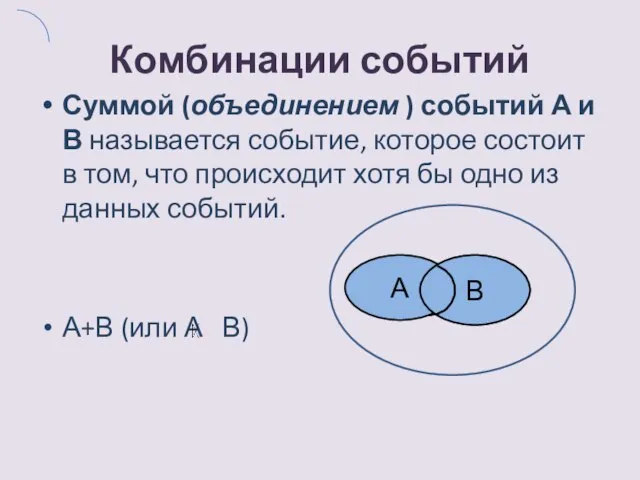
- 7. Комбинации событий Суммой (объединением ) событий А и В называется событие, которое состоит в том, что
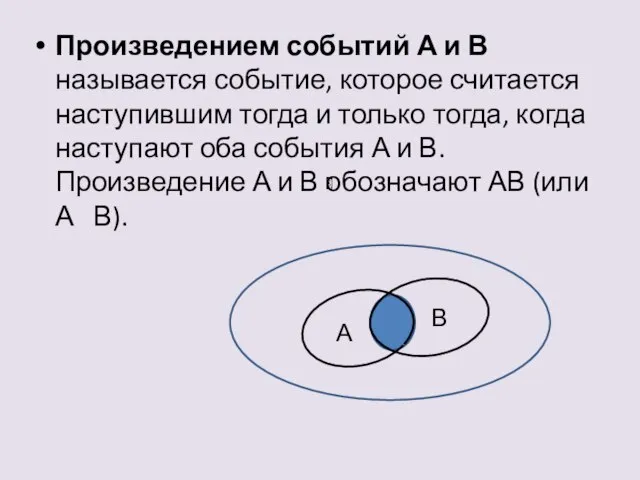
- 8. Произведением событий А и В называется событие, которое считается наступившим тогда и только тогда, когда наступают
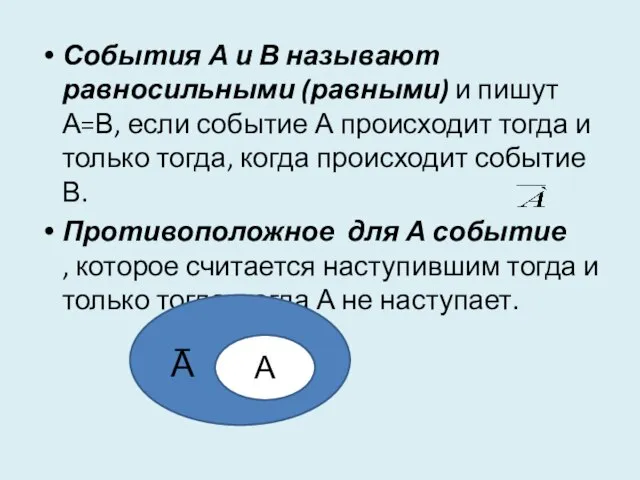
- 9. События А и В называют равносильными (равными) и пишут А=В, если событие А происходит тогда и
- 11. Скачать презентацию





 Учет капитальных вложений. Нормативные документы Долгосрочные
Учет капитальных вложений. Нормативные документы Долгосрочные Муром
Муром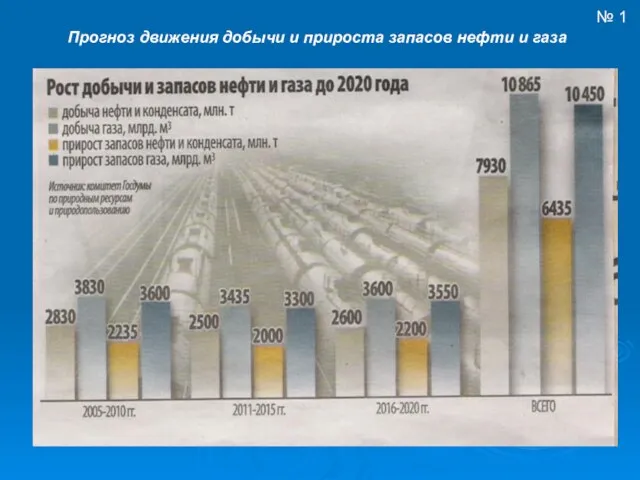 Прогноз движения добычи и прироста запасов нефти и газа
Прогноз движения добычи и прироста запасов нефти и газа Применение производной к исследованию функции.
Применение производной к исследованию функции. Лaтвия на пути к переходу на единую валюту
Лaтвия на пути к переходу на единую валюту Муниципальное общеобразовательное учреждение «Школа № 33» г.о.Саранск Комплексно – целевая программа «Здоровье»
Муниципальное общеобразовательное учреждение «Школа № 33» г.о.Саранск Комплексно – целевая программа «Здоровье» Бунт четырнадцати
Бунт четырнадцати Почему так названы животные
Почему так названы животные ГБоу сош «Школа здоровья» № 883
ГБоу сош «Школа здоровья» № 883 Китайский язык (по учебнику Сизовой А.А.)
Китайский язык (по учебнику Сизовой А.А.) Античный костюм Древней Греции
Античный костюм Древней Греции Недостаток витаминов укорачивает жизнь.
Недостаток витаминов укорачивает жизнь. Отчет по выездной практике
Отчет по выездной практике Малый уголок великой России Диво дивное
Малый уголок великой России Диво дивное Как эффективно убить социальную медиа
Как эффективно убить социальную медиа Автоматы практика
Автоматы практика Как наша прожила б планета Как люди жили бы на ней Без теплоты, магнита, света И электрических лучей!
Как наша прожила б планета Как люди жили бы на ней Без теплоты, магнита, света И электрических лучей! Презентация на тему Династия Романовых
Презентация на тему Династия Романовых Мастера печатных дел
Мастера печатных дел 1 Краткий обзор рекламной активности в группах C02 «Гипотензивные средства» в медицинской прессе и R06 «Антигистаминные средства для
1 Краткий обзор рекламной активности в группах C02 «Гипотензивные средства» в медицинской прессе и R06 «Антигистаминные средства для Исследование Северной Америки
Исследование Северной Америки Эшмоловский музей
Эшмоловский музей Условные предложения
Условные предложения Ice Kit. Доставка мороженого по Москве
Ice Kit. Доставка мороженого по Москве Основные средства организации
Основные средства организации Родительское собрание для групп СПО. Банковское дело. Страховое дело
Родительское собрание для групп СПО. Банковское дело. Страховое дело Презентация на тему Героическая страница моего края
Презентация на тему Героическая страница моего края «Игра на уроках обществознания и права»
«Игра на уроках обществознания и права»