Содержание
- 2. Встречаясь в жизни с различными событиями, мы часто даем оценку степени их достоверности. При этом произносим.
- 3. Вопрос о возможности измерения степени достоверности наступления какого-либо события задавали себе многие ученые Основателями теории вероятности
- 4. Наблюдая за игрой в кости, Б. Паскаль высказал идею измерения степени уверенности в выигрыше некоторым числом.
- 5. Вероятность события Если принять возможность наступления достоверного события за 1, то возможность появления, например, шестерки в
- 6. Вероятность события Если буквой А обозначить событие – «выпало 6 очков» при одном бросании игральной кости,
- 7. Задача Поверхность рулетки разделена диаметрами на 4 части. Найти вероятность того, что раскрученная стрелка рулетки остановится
- 8. Вероятность события Помимо рассмотренных элементарных событий можно рассматривать и более сложные события. Например, «выпадение четного числа
- 9. Вероятность события Если в некотором испытании существует n равновозможных попарно несовместных исхода и m из них
- 10. Задача Найти вероятность появления при одном бросании кости числа очков, большего 4 Событию А – «появление
- 11. Задача Поверхность рулетки разделена На 8 равных частей. Найти вероятность того, что после раскручивания стрелка рулетки
- 12. Если событие А - достоверное, то ему благоприятствуют все возможные исходы испытания, т. e. m =
- 13. Задача Перечислите все элементарные возможные события, которые могут произойти в результате: а) подбрасывания монеты б) подбрасывания
- 15. Скачать презентацию












 Отрасли права
Отрасли права Sistemul solar
Sistemul solar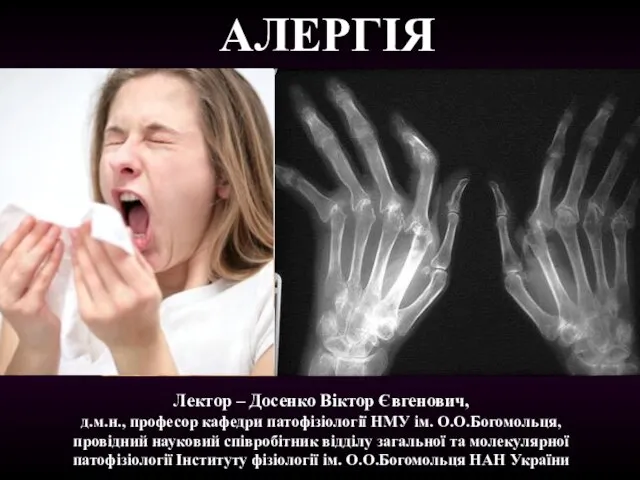 АЛЕРГІЯ
АЛЕРГІЯ Основные виды банковских рисков
Основные виды банковских рисков  Собор Василия Блаженного.
Собор Василия Блаженного. Ольховский И. А., Бабушкин В.А., Малахов В.Н *, Исхаков Т.Р. РОО "Красноярская краевая ассоциация медицинской лабораторной диагностик
Ольховский И. А., Бабушкин В.А., Малахов В.Н *, Исхаков Т.Р. РОО "Красноярская краевая ассоциация медицинской лабораторной диагностик МОУ «Афанасовская СОШ Корочанского района Белгородской области»
МОУ «Афанасовская СОШ Корочанского района Белгородской области» HARWEST GROUP. Поставщик кабельно-проводниковой и электротехнической продукции
HARWEST GROUP. Поставщик кабельно-проводниковой и электротехнической продукции Генные технологии и биоэтика
Генные технологии и биоэтика Психические процессы
Психические процессы Ценник. Наименование. Цена
Ценник. Наименование. Цена Слышишь голос соловья? Это - Родина твоя. Видишь звездочки Кремля? Это - Родина твоя. Школа, где твои друзья, Это - Родина твоя. Руки ма
Слышишь голос соловья? Это - Родина твоя. Видишь звездочки Кремля? Это - Родина твоя. Школа, где твои друзья, Это - Родина твоя. Руки ма Презентация на тему Музыкальная живопись и живописная музыка (5 класс)
Презентация на тему Музыкальная живопись и живописная музыка (5 класс) Квадратные уравнения
Квадратные уравнения Бизнес-геймификация на личной странице ВКонтакте. Лиды на автомате за счёт автоматизации и личного бренда
Бизнес-геймификация на личной странице ВКонтакте. Лиды на автомате за счёт автоматизации и личного бренда Великая Отечественная война
Великая Отечественная война Презентация на тему Печоро-Илычский заповедник
Презентация на тему Печоро-Илычский заповедник Slide 1 BA-BU
Slide 1 BA-BU The hippies
The hippies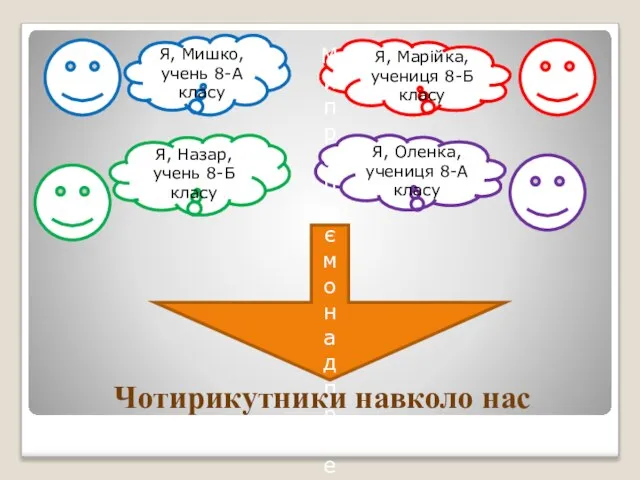 Я, Мишко, учень 8-А класу Я, Марійка, учениця 8-Б класу Я, Назар, учень 8-Б класу Я, Оленка, учениця 8-А класу Ми працюємо над проектом Чоти
Я, Мишко, учень 8-А класу Я, Марійка, учениця 8-Б класу Я, Назар, учень 8-Б класу Я, Оленка, учениця 8-А класу Ми працюємо над проектом Чоти Салат из крабовых палочек с кукурузой
Салат из крабовых палочек с кукурузой Пиявки
Пиявки Прямой поставщик товаров из Китая
Прямой поставщик товаров из Китая Преимущества сотрудничества с «Миром рекламы» по размещению в Интернете
Преимущества сотрудничества с «Миром рекламы» по размещению в Интернете Гиппократ. Описания свойств сангвиников, холериков, флегматиков
Гиппократ. Описания свойств сангвиников, холериков, флегматиков Цвет. Основы цветоведения
Цвет. Основы цветоведения Япония 日本
Япония 日本 Страна под настроение
Страна под настроение