Вихревой характер магнитного поля. Магнитный поток

ОГЛАВЛЕНИЕ
16.1. Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток
16.2. Сила Ампера
16.3. Работа по перемещению проводника с током в магнитном поле
16.4. Сила Лоренца
16.5. Определение удельного заряда электрона

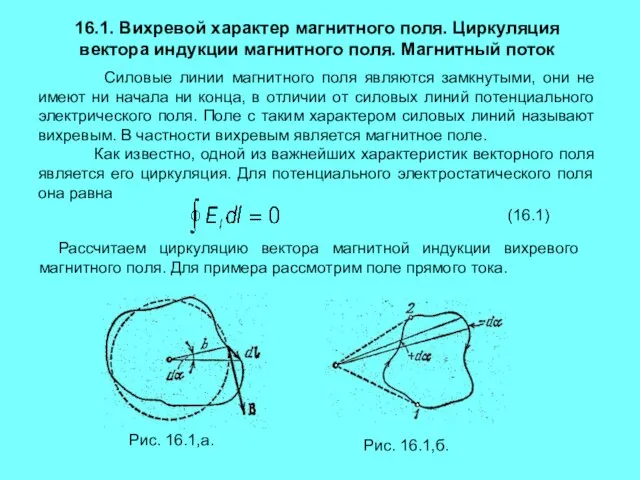
16.1. Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток Силовые линии магнитного поля являются замкнутыми, они не имеют ни начала ни конца, в отличии от силовых линий потенциального электрического поля. Поле с таким характером силовых линий называют вихревым. В частности вихревым является магнитное поле.
Как известно, одной из важнейших характеристик векторного поля является его циркуляция. Для потенциального электростатического поля она равна
Рассчитаем циркуляцию вектора магнитной индукции вихревого магнитного поля. Для примера рассмотрим поле прямого тока.
Рис. 16.1,а.
Рис. 16.1,б.
(16.1)

Пусть замкнутый контур лежит в плоскости, перпендикулярной к току (рис. 16.1,а; ток перпендикулярен к плоскости чертежа и направлен за чертеж). В каждой точке контура вектор
направлен по касательной к окружности,
проходящей через эту точку. Заменим в выражении для циркуляции
через BdlB (dlB – проекция элемента контура на направление вектора
). Из
рисунка видно, что dlB равно bdα, где b – расстояние от провода с током до
dα – угол, на который поворачивается радиальная прямая при перемещении вдоль контура на отрезок
Таким образом, для В получим
Имеем

При обходе по контуру, охватывающему ток, радиальная прямая все время поворачивается в одном направлении, поэтому
Иначе обстоит дело, если ток не охватывается контуром (рис. 16.1,б). В этом случае при обходе по контуру радиальная прямая поворачивается сначала в одном направлении (участок 1-2), а затем в противоположном (участок 2-1), вследствие чего
Учтя этот результат, можно написать
где под I следует подразумевать ток, охватываемый контуром. Если контур тока не охватывает, циркуляция вектора
равна нулю.
Обобщая конечный результат для циркуляции магнитного поля, созданного токами i1, i2, ... ,ik, приходим к формуле
(16.2)
(16.3)

Магнитный поток.
По определению, магнитный поток вычисляется по формуле
В СИ магнитный поток измеряется в Веберах (Вб)
Если рассмотреть замкнутую поверхность S, то поток линий магнитной индукции через нее равен нулю:
Рис. 16.2.
(16.5)
К оглавлению
(16.4)
(16.5)

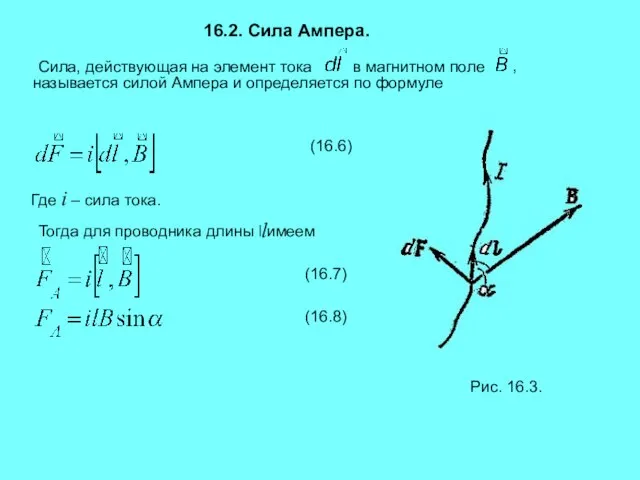
16.2. Сила Ампера.
Сила, действующая на элемент тока
в магнитном поле
называется силой Ампера и определяется по формуле
,
Где i - сила тока
Тогда для проводника длины l имеем
Рис. 16.3.
(16.6)
(16.7)
(16.8)
Где i – сила тока.
l

Направление силы Ампера мы узнаем по правилу левой руки.
Направление линий магнитной индукции входит в левую ладонь.
Пальцы вытянуты по направлению тока.
Отогнутый большой палец указывает направление силы Ампера.
Рис. 16.4.

Применим правило левой руки для объяснения опыта Ампера (взаимодействие двух параллельных проводников с током):
Рис. 16.5.
На рисунке показано направление силы Ампера в случаях, когда токи i1 и i2 параллельны и антипараллельны.
В системе СИ основной единицей силы тока является ампер ([i]=A). Под силой тока в один ампер понимают силу такого неизменяющегося тока, который, протекая по двум бесконечно длинным и тонким проводникам, разнесенным в вакууме на расстояние 1м друг от друга, вызывает силу взаимодействия 2⋅10-7 Н на каждый метр длины проводника.
К оглавлению

16.3. Работа по перемещению проводника с током в магнитном поле.
Введя понятие потока магнитной индукции, можно рассчитать работу по перемещению проводника с током в магнитном поле. Пусть проводник CD может передвигаться под действием силы Ампера . Тогда работа по его перемещению будет равна
где
Рис. 16.6.
К оглавлению
– изменение магнитного потока.
– т. н. “покрытая” площадь,
(16.9)

16.4. Сила Лоренца
Рассчитаем силу, которая действует на один отдельно взятый движущийся заряд q (рис. 16.7)
Рис. 16.7.
Сила Ампера
Сила тока в проводнике
Плотность тока
Осуществим подстановки:
или, в векторной форме:
(16.10)
(16.11)
(16.12)

Если движется положительный заряд (q>0), то
Если движется отрицательный заряд (q<0), то
Рассмотрим частные случаи движения заряженной частицы в магнитном поле.
1.
Движение прямолинейное и равномерное,
т. е.
Рис. 16.8.
Уравнение движения

2.
Траектория движения— окружность.
Рис. 16.9.
Период вращения по определению
Подставив (16.14) в (16.15), получим
(16.13)
(16.14)
(16.15)
(16.16)

3. Частица влетает под произвольным углом α.
Выбираем систему координат и разложим вектор скорости на две составляющие.
Применим принцип независимости движений Галилея.
(16.17)

Траектория — винтовая линия.
Параметры: радиус винта и шаг.
Шаг винта — расстояние, которое проходит заряд вдоль оси винта за время Т.
Рис. 16.10.
Измерив экспериментально параметры траектории, можно определить величину удельного заряда частицы q/m.
К оглавлению
(16.18)

Метод магнитной фокусировки
Буш применил для определения удельного заряда электрона метод магнитной фокусировки. Суть этого метода заключается в следующем. Допустим, что в однородном магнитном поле вылетает из некоторой точки слегка расходящийся пучок электронов, имеющих одинаковую по величине скорость v, Направления, по которым вылетают электроны, образуют с направлением В небольшие углы α. Электроны в этом случае движутся по спиральным траекториям, совершая за одинаковое время (16.17) полный оборот и смещаясь вдоль направления поля на расстояние (16.18). Вследствие малости углов α расстояния (16.18) для данных электронов оказываются практически одинаковыми и равными vT (для малых углов cosα≈1). Следовательно, слегка расходящийся пучок сфокусируется в точке, отстоящей от точки вылета электронов на расстояние
(16.19)
16.5. Определение удельного заряда электрона

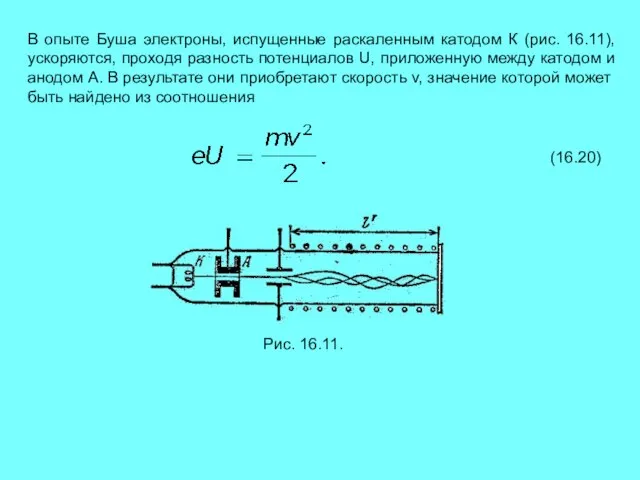
В опыте Буша электроны, испущенные раскаленным катодом К (рис. 16.11), ускоряются, проходя разность потенциалов U, приложенную между катодом и анодом А. В результате они приобретают скорость v, значение которой может быть найдено из соотношения
(16.20)
Рис. 16.11.