Волгодонск

Решение квадратных уравнений
Цели:
Обобщить знания по теме «Решение уравнений»
Повторить способы решения квадратных уравнений
Закрепить навыки решения квадратных уравнения

Ответь на вопросы:
Как называется равенство, содержащее переменную?
Как называется число, обращающее уравнение в верное равенство?
Какое уравнение называется квадратным уравнением?
Как называется квадратное уравнение в котором хотя бы один из коэффициентов а или в равен ноль?
Назовите виды неполных квадратных уравнений.
Может ли уравнение вида не иметь корней?
Каков алгоритм решения уравнения , где
а,в,с – некоторые числа, причем а ≠ 0?
Какое уравнение называется приведенным квадратным уравнением?
Что гласит теорема Виета?
Теорема обратная теореме Виета?

Математическое путешествие по Волге.

Криптографическая таблица

Ярославль
Ярославль

Кострома

Нижний Новгород

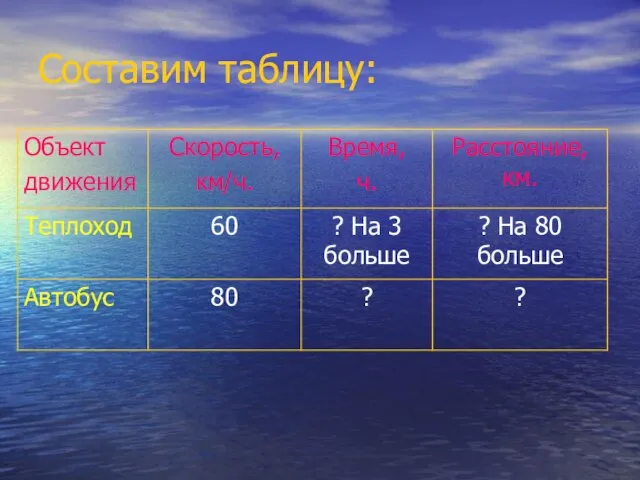
Решите задачу:
Путь по Волге от Нижнего Новгорода до Казани на 80 км длиннее, чем по шоссе. Две туристические группы собрались на экскурсию в Казань. Первая группа отправилась на теплоходе, чтобы полюбоваться красивейшими пейзажами волжских берегов, а вторая группа – на автобусе. Чтобы попасть в Казань одновременно, любители речных прогулок выехали на 3 часа раньше. Найти длину Волги на участке от Нижнего Новгорода до Казани, если скорость теплохода 60 км/ч, а скорость автобуса 80 км/ч.

Составим таблицу:

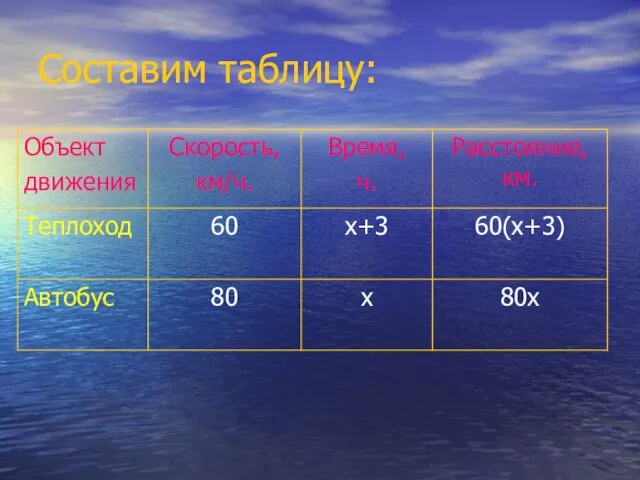
Составим таблицу:

Решение задачи:
60(х + 3) - 80х = 80 60х + 180 – 80х = 80;
60х – 80х = 80 - 180 ;
- 20х = - 100;
х = 5(ч) – был в пути автобус
5 + 3 = 8(ч) – был в пути теплоход.
60 · 8 = 480 (км) – длина Волги на участке от Нижнего Новгорода до Казани.
Ответ: 480 км.

Казань

Итоги урока.
Закрепили навыки решения неполных квадратных уравнений;
Повторили схему решения задач на движение;
Узнали много нового о волжских городах и ученых-математиках, живших в этих городах.