Содержание
- 2. Современная вычислительная среда. Глобальная модель циркуляции «атмосфера-океан»(МITcgm)-107-109 узлов(кубов). Обтекание «Аэробуса»-107 тетраэдров. Биотомограф-1000х1000х1000(109) вокселов. Фармацевтика- триангуляция молекулярной
- 3. Геометрико - топологические особенности. Меры по сохранению устойчивости решения(число и геометрия тетраэдров). Проведение оперативных преобразований среды.(кластеризация
- 4. Digital geometry and topology Discrete differential geometry США ( MIT, Caltech, Stanford) Франция(INRIA) Германия (Un.Gumbold) Швеция
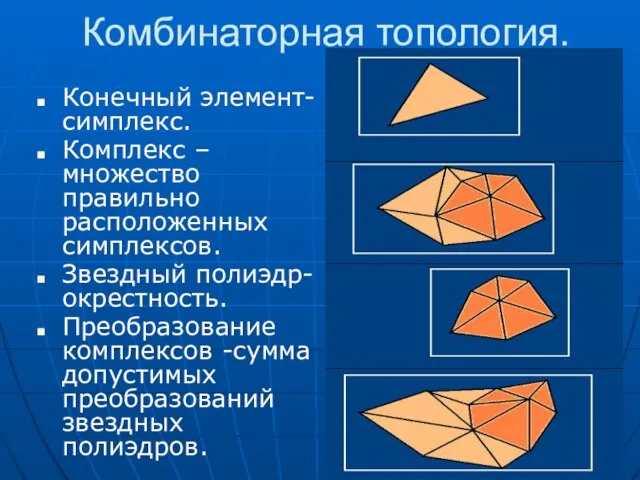
- 6. Комбинаторная топология. Конечный элемент-симплекс. Комплекс –множество правильно расположенных симплексов. Звездный полиэдр-окрестность. Преобразование комплексов -сумма допустимых преобразований
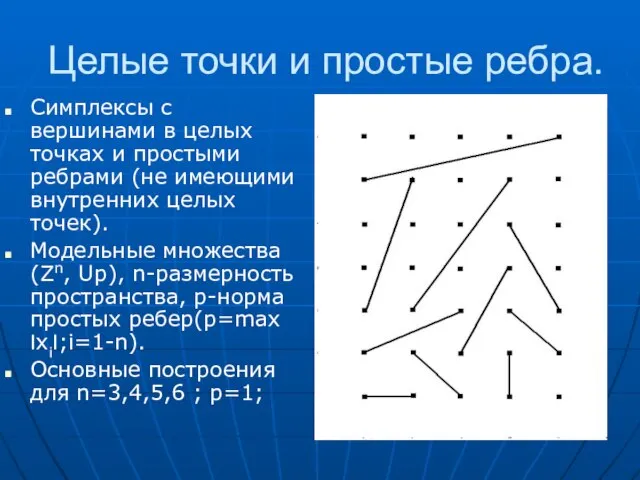
- 7. Целые точки и простые ребра. Симплексы с вершинами в целых точках и простыми ребрами (не имеющими
- 8. Основная последовательность базисных построений. Построение однородных звездчатых полиэдров (стереоэдров) на простых симплексах. Покрытие такими полиэдрами всего
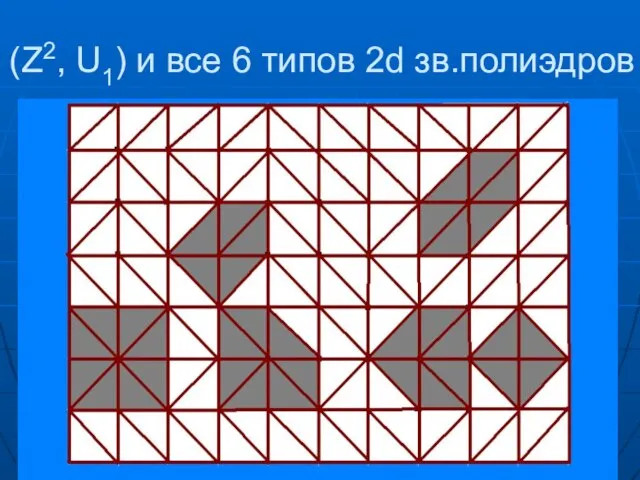
- 9. (Z2, U1) и все 6 типов 2d зв.полиэдров
- 10. Перестройки разбиения - выделение параллелограммов и замена диагоналей.
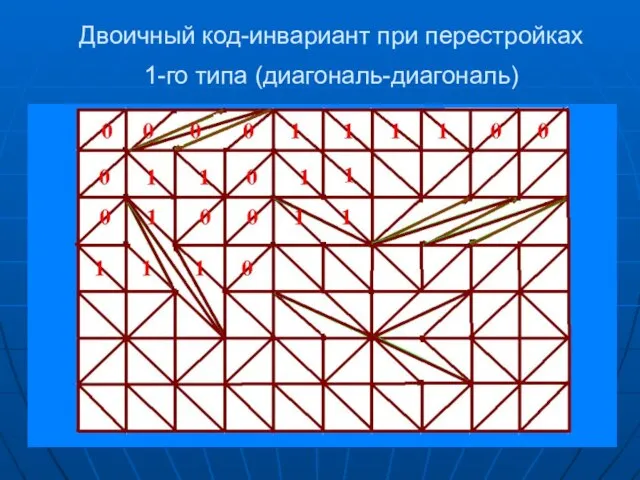
- 11. Двоичный код-инвариант при перестройках 1-го типа (диагональ-диагональ)
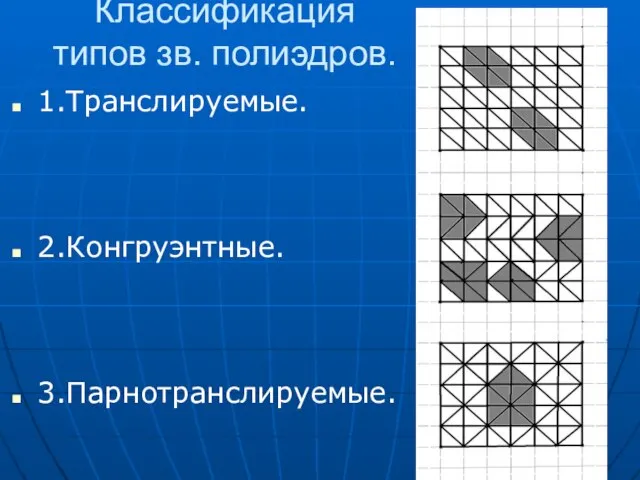
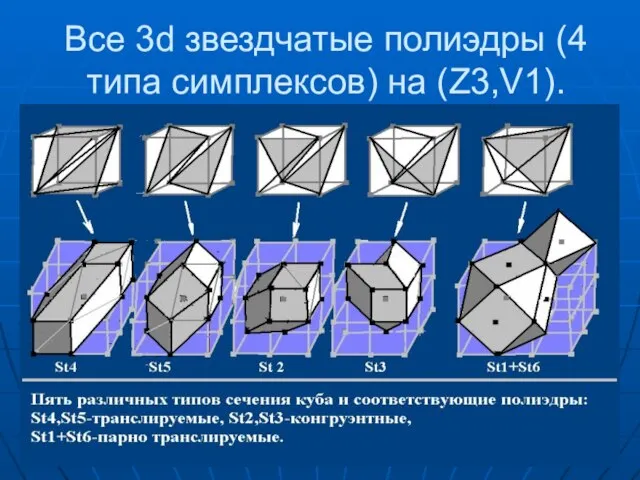
- 12. Классификация типов зв. полиэдров. 1.Транслируемые. 2.Конгруэнтные. 3.Парнотранслируемые.
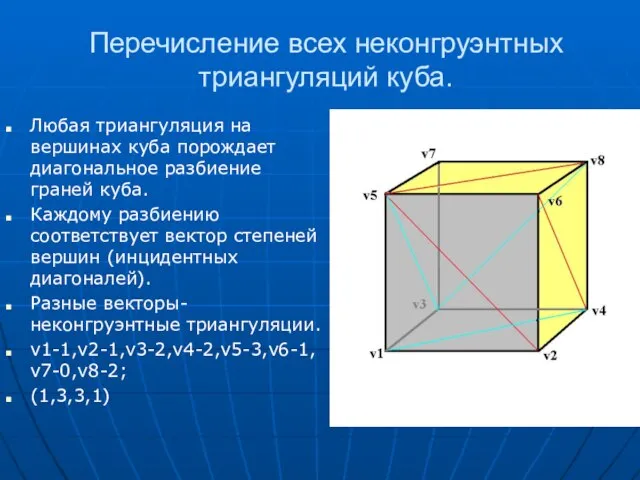
- 13. Перечисление всех неконгруэнтных триангуляций куба. Любая триангуляция на вершинах куба порождает диагональное разбиение граней куба. Каждому
- 14. Диофантовы уравнения. i-число диагоналей сходящихся к вершине. xi-число вершин с i сходящимися диагоналями. Σ xi =8;
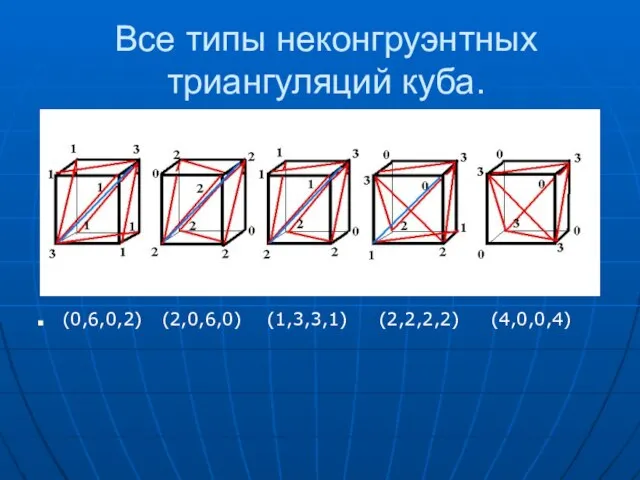
- 15. Все типы неконгруэнтных триангуляций куба. (0,6,0,2) (2,0,6,0) (1,3,3,1) (2,2,2,2) (4,0,0,4)
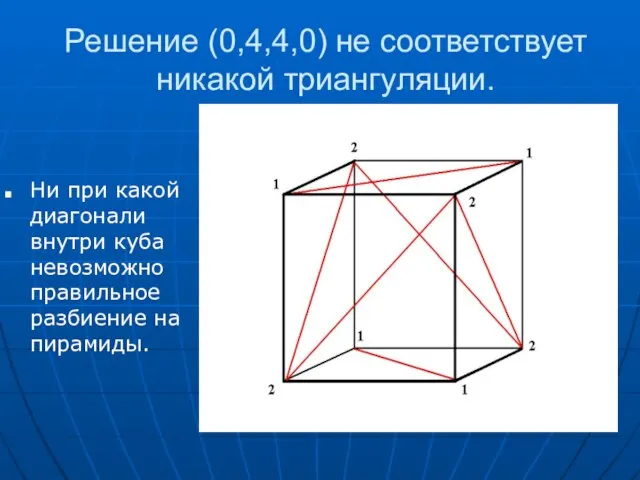
- 16. Решение (0,4,4,0) не соответствует никакой триангуляции. Ни при какой диагонали внутри куба невозможно правильное разбиение на
- 17. Все 3d звездчатые полиэдры (4 типа симплексов) на (Z3,V1).
- 18. Разбиение кубов проекциями-транслируемая полиэдризация R3. Разбиение единичного куба на 6 тетраэдров-симплексов.
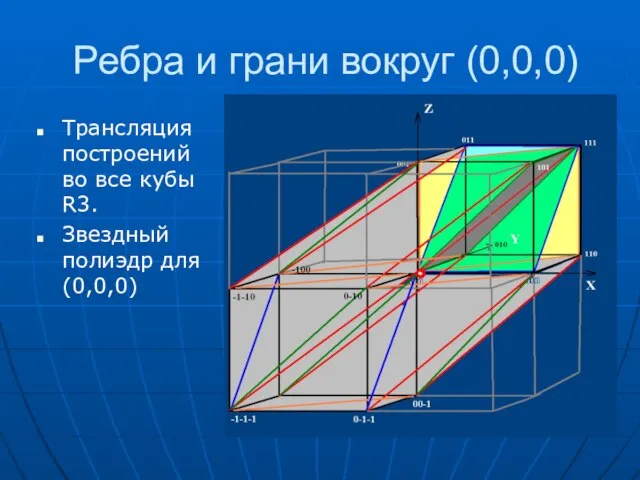
- 19. Ребра и грани вокруг (0,0,0) Трансляция построений во все кубы R3. Звездный полиэдр для (0,0,0)
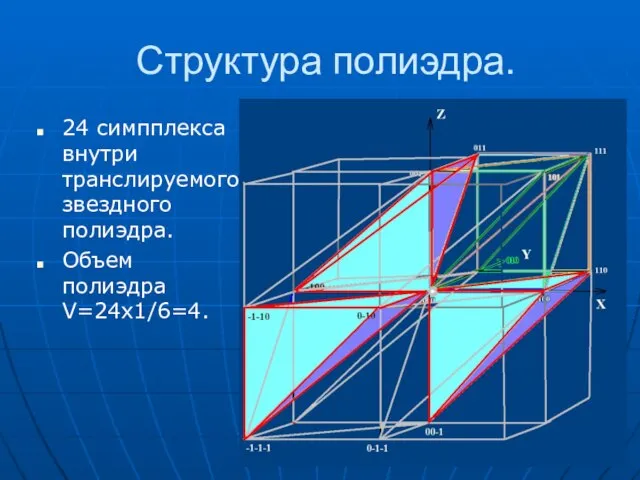
- 20. Cтруктура полиэдра. 24 симпплекса внутри транслируемого звездного полиэдра. Объем полиэдра V=24x1/6=4.
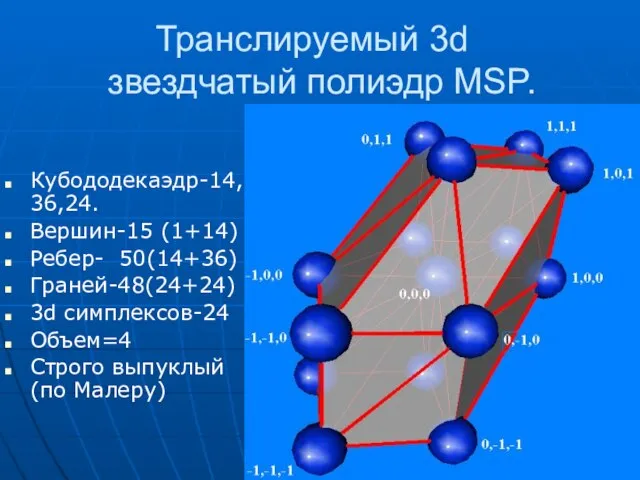
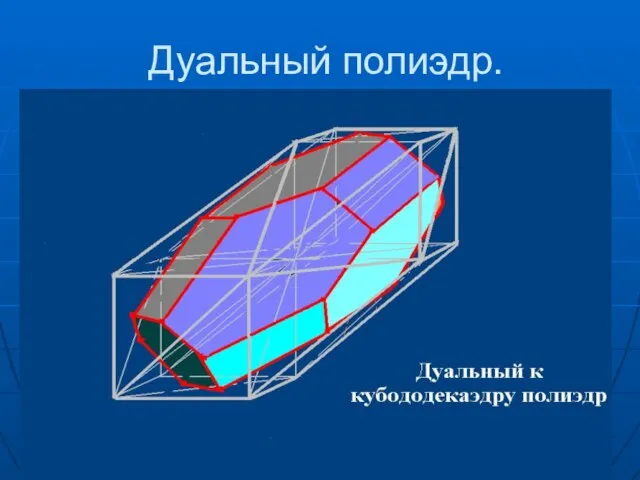
- 21. Транслируемый 3d звездчатый полиэдр MSP. Кубододекаэдр-14,36,24. Вершин-15 (1+14) Ребер- 50(14+36) Граней-48(24+24) 3d cимплексов-24 Объем=4 Строго выпуклый
- 22. Дуальный полиэдр.
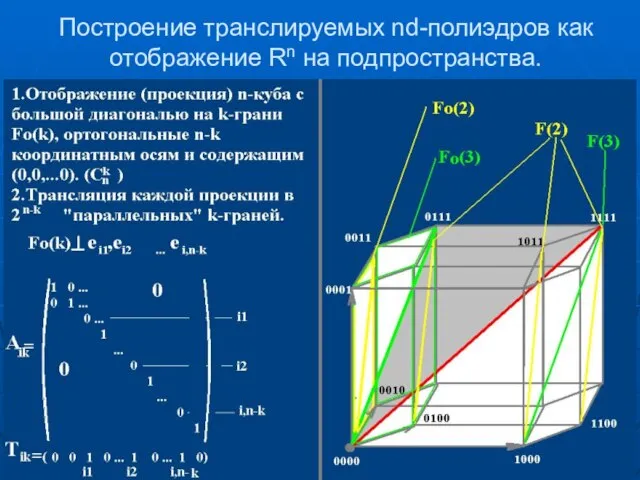
- 23. Построение транслируемых nd-полиэдров как отображение Rn на подпространства.
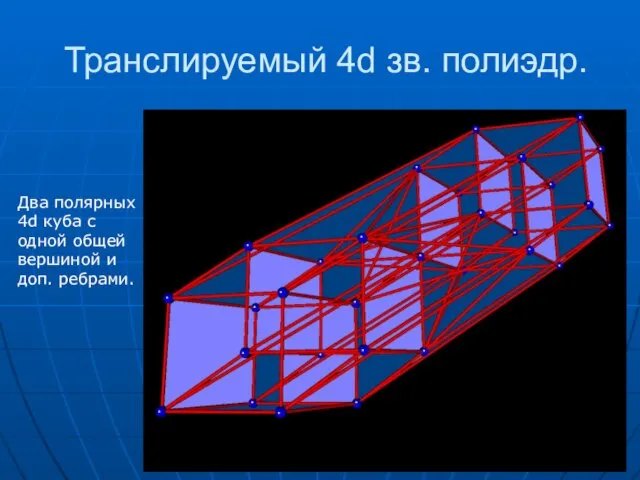
- 24. Транслируемый 4d зв. полиэдр. Два полярных 4d куба с одной общей вершиной и доп. ребрами.
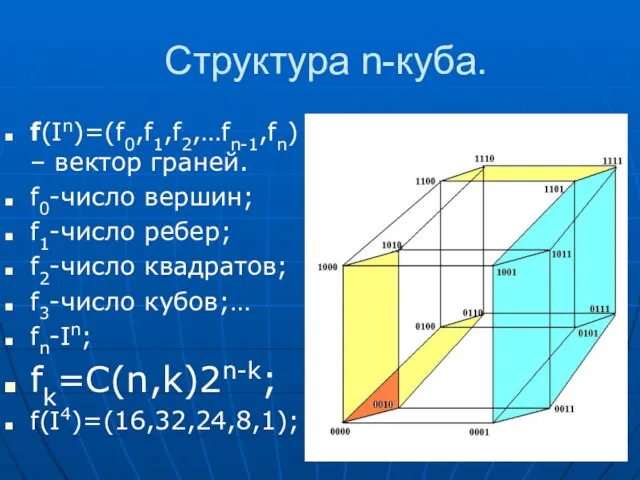
- 25. Структура n-куба. f(In)=(f0,f1,f2,…fn-1,fn) – вектор граней. f0-число вершин; f1-число ребер; f2-число квадратов; f3-число кубов;… fn-In; fk=C(n,k)2n-k;
- 26. Характеристика Эйлера-Пуанкаре Формула Эйлера:В-Р+Г=2 Топологический инвариант χ=f0-f1+f2-f3+…+(-1)n-1fn-1;
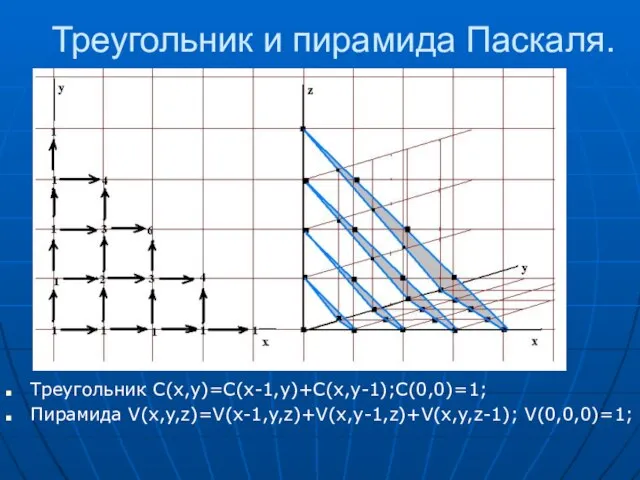
- 27. Треугольник и пирамида Паскаля. Треугольник C(x,y)=C(x-1,y)+C(x,y-1);C(0,0)=1; Пирамида V(x,y,z)=V(x-1,y,z)+V(x,y-1,z)+V(x,y,z-1); V(0,0,0)=1;
- 28. Триномиальные коэффициенты. (a+b+c)n V(n,k,l)albkcn-k-l l=x;k=y;n=x+y+z; V(n,k,l)= n!/l!k!(n-k-l)! Σ V(n,k,l)=C(n,k)2n-k; l=1-(n-k); ΣV(n,k,l)=fk; (16,32,24,8)
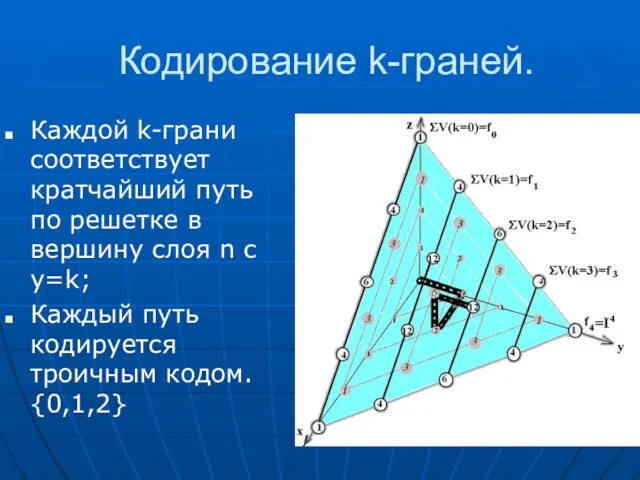
- 29. Кодирование k-граней. Каждой k-грани соответствует кратчайший путь по решетке в вершину слоя n c y=k; Каждый
- 30. Кодировка I4 0000 в 0001 в 0002 р 0010 в 0011 в 0012 р 0020 р
- 31. Геометрическая интерпретация Код 2120 Ребра 0020 и 2000 -> грань 2020 Грань 2020 транслируется из (0000)
- 32. Генерация примитивной триангуляции (путевые симплексы) Симметрическая группа подстановок Sn. si € Sn 1 2 3 …
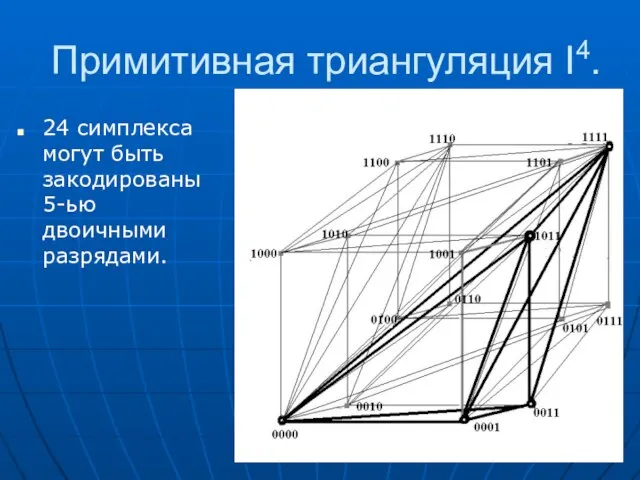
- 33. Примитивная триангуляция I4. 24 cимплекса могут быть закодированы 5-ью двоичными разрядами.
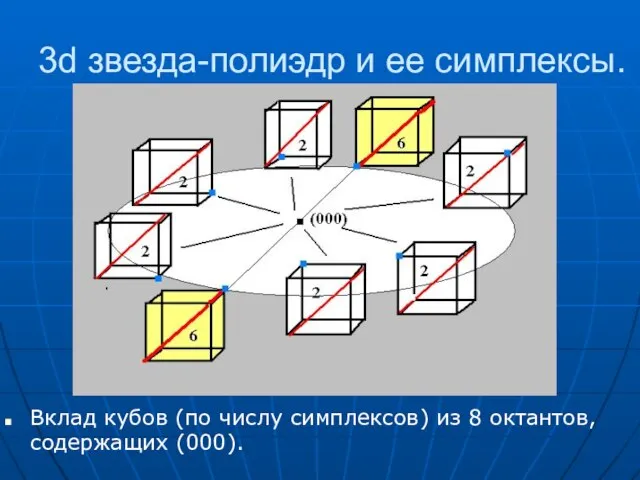
- 34. 3d звезда-полиэдр и ее симплексы. Вклад кубов (по числу симплексов) из 8 октантов, содержащих (000).
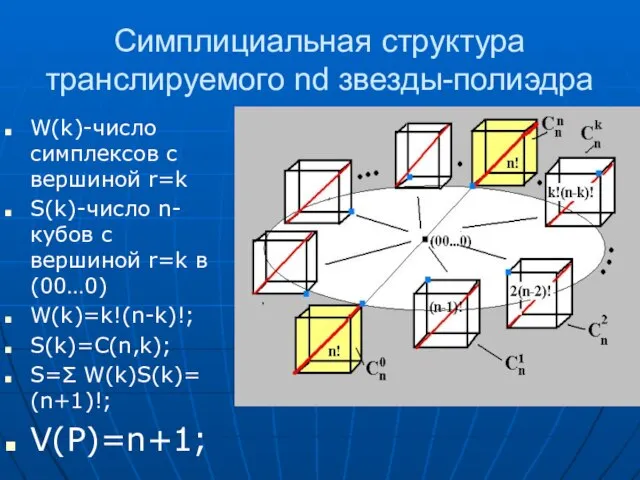
- 35. Симплициальная структура транслируемого nd звезды-полиэдра W(k)-число симплексов с вершиной r=k S(k)-число n-кубов с вершиной r=k в
- 36. Кодирование симплексов . 1234,1243,1324,1342,1423,1432, 0 1 2 3 4 5 2134,2143,2314,2341,2413,2431, 5 7 8 9 10
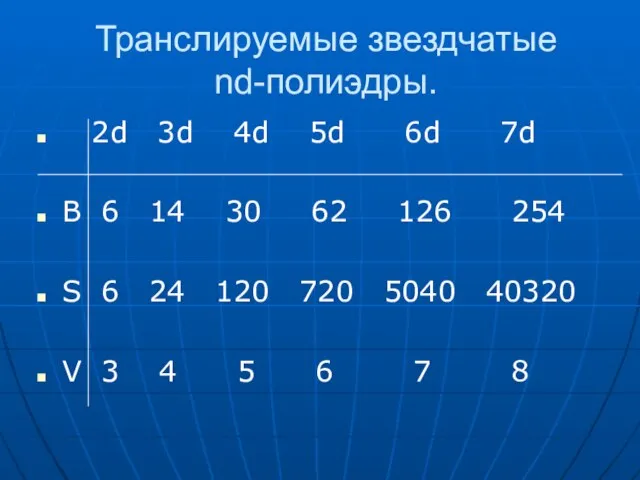
- 37. Транслируемые звездчатые nd-полиэдры. 2d 3d 4d 5d 6d 7d В 6 14 30 62 126 254
- 38. Гомотопные расширения и сжатия комплексов-сумма преобразований MSP на границе комплексов. Топологический контроль-проверка связности в MSP до
- 39. Допустимые преобразования без склеек и разрывов. Расширение «желтого» без склеек и разрывов «желтого» и «красного» зависит
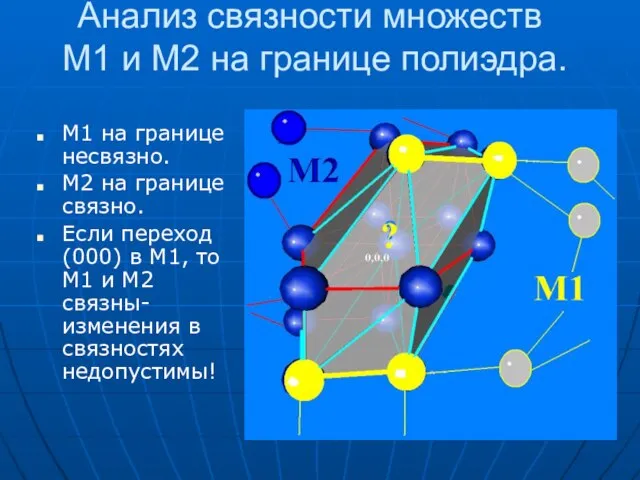
- 40. Анализ связности множеств М1 и М2 на границе полиэдра. М1 на границе несвязно. М2 на границе
- 41. Три 2d комплекса
- 42. Расширение черного.
- 43. Расширение черного.
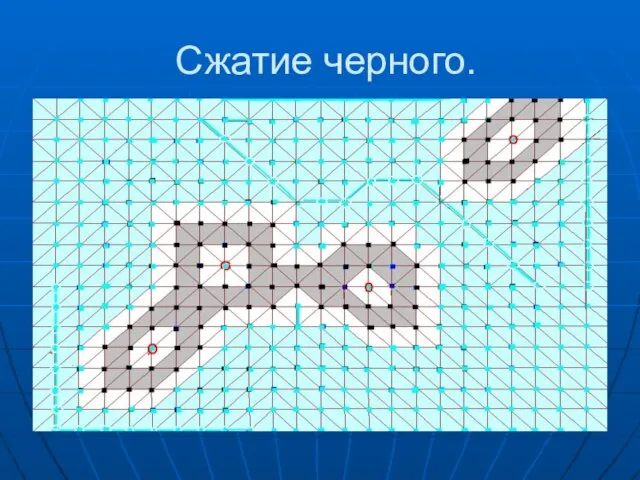
- 44. Сжатие черного.
- 45. Приближение к евклидовой метрике на Zn. Метрика на ребрах звездчатых полиэдров (многогранная метрика) далека от евклидовой.
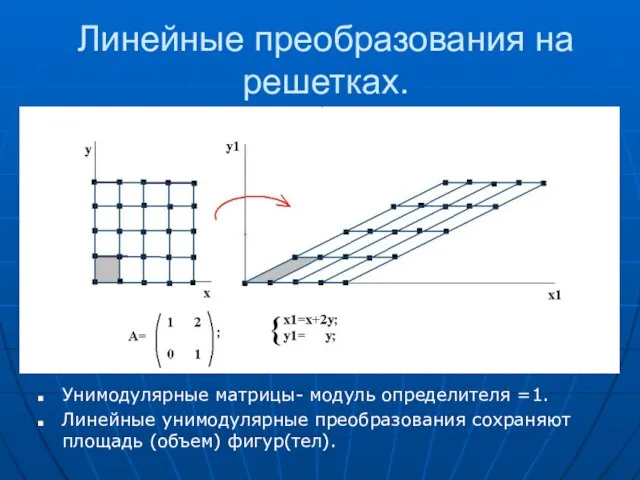
- 46. Линейные преобразования на решетках. Унимодулярные матрицы- модуль определителя =1. Линейные унимодулярные преобразования сохраняют площадь (объем) фигур(тел).
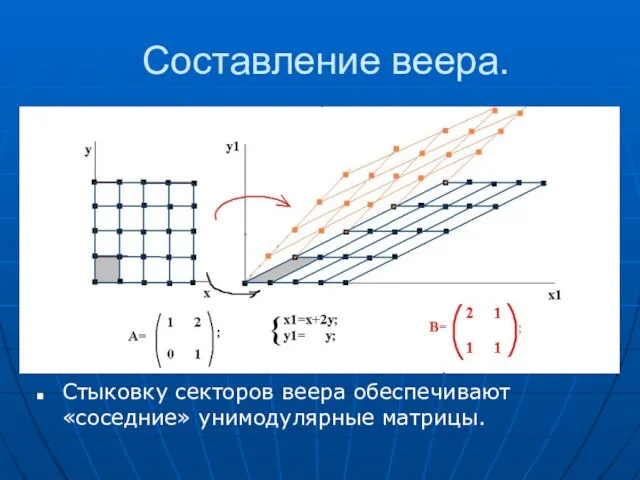
- 47. Составление веера. Стыковку секторов веера обеспечивают «соседние» унимодулярные матрицы.
- 48. Несократимые дроби и простые ребра (веер Фарея). В каждом секторе целые точки образуют решетки с базисами
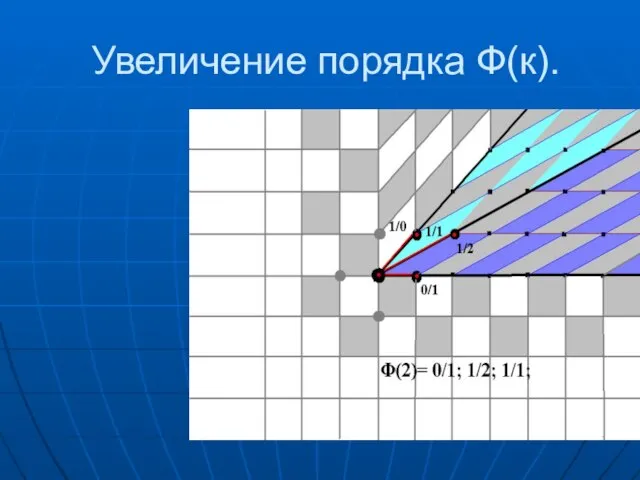
- 49. Увеличение порядка Ф(к).
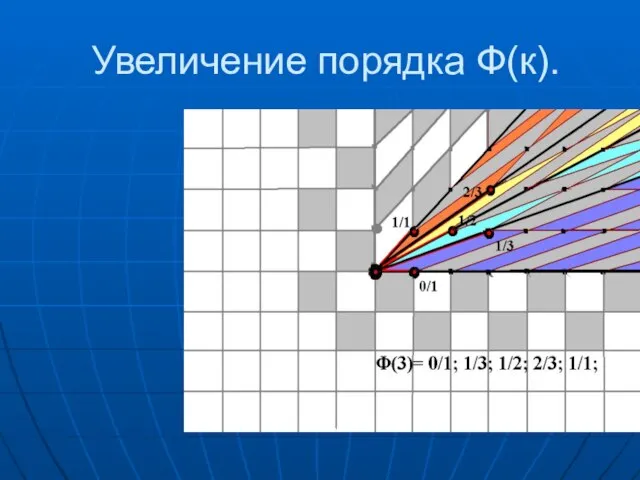
- 50. Увеличение порядка Ф(к).
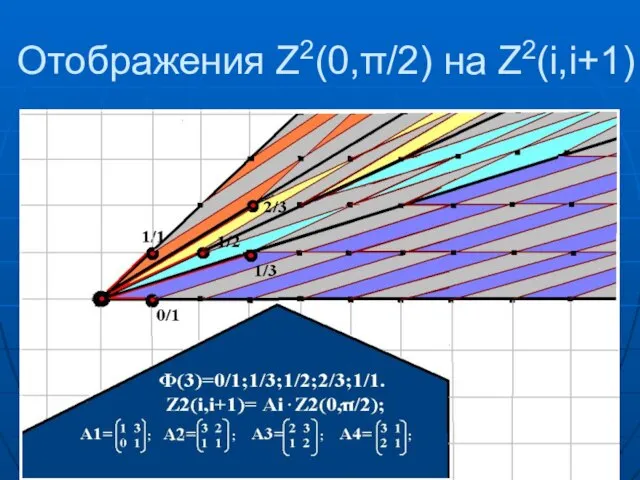
- 51. Отображения Z2(0,π/2) на Z2(i,i+1)
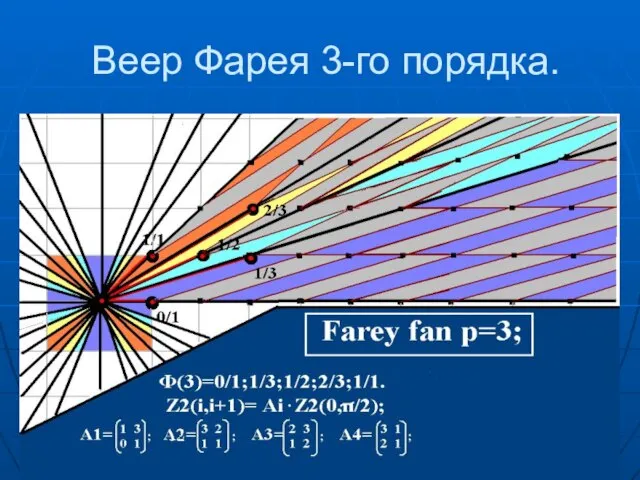
- 52. Веер Фарея 3-го порядка.
- 53. Неравномерность уменьшения углов в секторах веера. Для веера Ф(3): Сектор ((0/1)(1/3))~1/3. Cектор ((1/3)(1/2))~1/6. Коррекция процедуры генерации
- 54. Приближение к евклидовой метрике. Для сектора веера с базисом bi,bj и углом φ: L=λ1ρ(bi)+λ2ρ(bj);на решетке, Le-евклидова
- 55. Для построения веера в Rn. Множество целочисленных квадратных матриц:{Ai}. Ai =1 сохраняет объемы. Бесконечная группа с
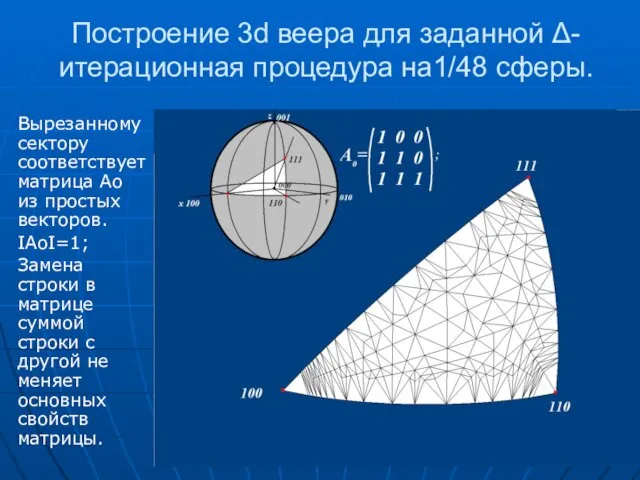
- 56. Построение 3d веера для заданной Δ-итерационная процедура на1/48 сферы. Вырезанному сектору соответствует матрица Ао из простых
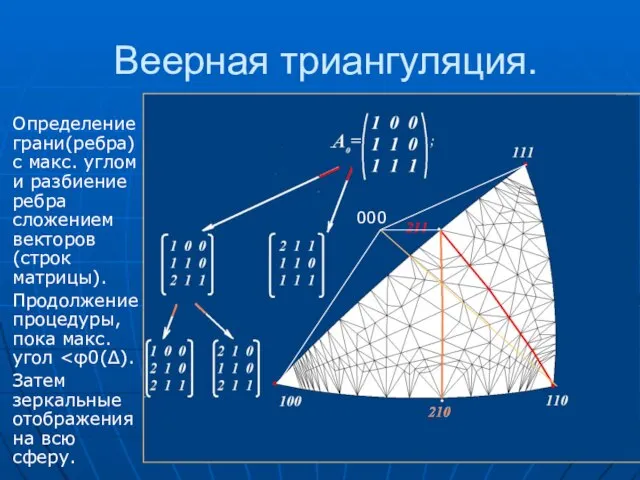
- 57. Веерная триангуляция. Определение грани(ребра) с макс. углом и разбиение ребра сложением векторов (строк матрицы). Продолжение процедуры,
- 58. Nd-случай. Для nd случая триангулируется (а затем и хранится в памяти) 1/2n n! – часть nd
- 59. Проекция 3d веера на сферу (для Δ=L-Le/Le=0,001) После зеркальных отображений 1/48 части на всю сферу. Веер
- 60. Сравнение по числу ребер 3d веера Фарея и решеточного расслоения . K 2 3 4 5
- 61. Основные операции прототипа топологического процессора. Задание решетки и метода полиэдризации. Задание границ и преград. Задание комплексов.
- 62. Построение «сферы» как 2d многообразия. Заданы центр «сферы» и преграды(2пластины). Построить «сферу» минимального радиуса. Условие: преграды
- 63. Ближайшие задачи. Перенос комплекса на кластер НИВЦ МГУ с целями: 1.Решение задач на решетках:3d-20003,4d-5004,5d-2005,6d-506. 2.Использование распараллеливания,
- 64. Основные ссылки. Л.С.Понтрягин. Основы комбинаторной топологии. П.С.Александров. Комбинаторная топология. Б.Н.Делоне. Теория стереоэдров. К.Чандрасекхаран. Введение в аналитическую
- 66. Скачать презентацию































 Презентация на тему Алюминий и сплавы алюминия
Презентация на тему Алюминий и сплавы алюминия Дизайн столярно-мебельных изделий
Дизайн столярно-мебельных изделий Напольная плитка
Напольная плитка Призначення та конструкція допоміжних елементів системи УТАС
Призначення та конструкція допоміжних елементів системи УТАС Как написать научную работу?
Как написать научную работу? Мастер-класс Тайм-менеджмент для учёных
Мастер-класс Тайм-менеджмент для учёных Доповідь заступника директора департаменту праці та соціального захисту
Доповідь заступника директора департаменту праці та соціального захисту Побуждение к аплодисментам
Побуждение к аплодисментам Промышленность мира
Промышленность мира ОБЩЕСТВЕННО – ПРОФЕССИОНАЛЬНАЯ АККРЕДИТАЦИЯ
ОБЩЕСТВЕННО – ПРОФЕССИОНАЛЬНАЯ АККРЕДИТАЦИЯ “…оград узор чугунный”Князева Елена Викторовнаучитель школы №8 «Музыка»
“…оград узор чугунный”Князева Елена Викторовнаучитель школы №8 «Музыка» Пещера Шове́
Пещера Шове́ презентациГЕВОЛЬ новинки 2020
презентациГЕВОЛЬ новинки 2020 В2 Прочитайте приведенный ниже текст, в котором ряд слов пропущен. Выберите из предлагаемого списка слова, которые необходимо вста
В2 Прочитайте приведенный ниже текст, в котором ряд слов пропущен. Выберите из предлагаемого списка слова, которые необходимо вста Радио Попова
Радио Попова Правоохранительная деятельность
Правоохранительная деятельность  Учет поступления и расхода товара в аптеке
Учет поступления и расхода товара в аптеке Предмет и методы социальной психологии как науки
Предмет и методы социальной психологии как науки Die Rechtsverhältnisse
Die Rechtsverhältnisse Основы государственной культурной политики Российской Федерации. Лекция 2
Основы государственной культурной политики Российской Федерации. Лекция 2 Римляне в повседневной жизни
Римляне в повседневной жизни Презентация на тему Почему снег скрипит
Презентация на тему Почему снег скрипит Безопасное поведение на улицах и дорогах
Безопасное поведение на улицах и дорогах Jelly for Jerry
Jelly for Jerry Can you swim?
Can you swim? Дождь
Дождь КАРТОННО-БУМАЖНЫЕ МАТЕРИАЛЫ И ТАРА
КАРТОННО-БУМАЖНЫЕ МАТЕРИАЛЫ И ТАРА Сюжетно-ролевые игры.
Сюжетно-ролевые игры.