Введение в организацию белковой структуры и молекулярное моделирование

Проблематика самоорганизации структуры белка
“Предсказание трехмерной структуры белка по его аминокислотной последовательности.”
“Каким образом белковая молекула самостоятельно организуется в свою третичную структуру?”
С середины прошлого столетия на этот вопрос еще не дан ответ

Белки могут сворачиваться в свои третичные структуры спонтанно
В растворах белковые молекулы самостоятельно организуются в трехмерные формы
Конечная трехмерная форма белка зависит от уровня минимальной свободной энергии системы «белок – растворитель». (Постулат Анфинсена)

Парадокс Левинтала
Можем предположить, что для каждой аминокислоты существует три варианта ее состояния в белке (α-спираль, β-слой и клубок). Если белок состоит из 100 аминокислот (аминокислотных остатков), тогда общее количество вариантов состояний будет:
3100 = 515377520732011331036461129765621272702107522001
≒ 5 x 1047.
Если требуется только 100 пс (10-10 с) для перехода из одного состояния в другое, тогда на перебор всех вариантов уйдет
5 x 1047 x 10-10 с ≒ 1.6 x 1030 лет.
А, сворачивание аминокислотной последовательности в третичную структуру происходит за время, измеряемое миллисекундами. Таким образом, белки самоорганизуются не через случайный подбор вариантов, а используют более изощренный путь.
Мы хотим проследить процесс сворачивания белка в третичную форму, используя технологию молекулярного моделирования.

Почему “Самоорганизация структуры белка” так важна?
Белки играют важные роли в живых организмах.
Некоторые белки напрямую связаны с заболеваниями. Информация о структуре белка необходима, чтобы объяснить и определить его функцию, а также, чтобы создать молекулу, которая бы связывалась с этим белком, если это необходимо в стратегии лечения.
На сегодня, полностью расшифрованы геномы (полные наборы генов) разных организмов и мы понимаем, что функции многих генов нам до сих пор неизвестны, а часть связана с разными заболеваниями.
Таким образом, знание процесса самоорганизации белка поможет нам исследовать функции этих генов, и создать эффективные лекарства против связанных с ними заболеваний.
В добавление к этому, это понимание покажет нам путь к созданию белков, у которых будут совсем новые функции, например, как новые наномашины.

Почему проблема “Самоорганизации структуры белка” так сложна?
С точки зрения компьютерного моделирования,
Сложно моделировать весь процесс самоорганизации белковой молекулы на уровне атомов, даже используя самые современные компьютеры.
Пока не ясно, достаточна ли точность параметров и значений функций энергии для моделирования процесса самоорганизации белка или нет.
…, позвольте мне пересказать диалог с Фрэнсисом в 1975 (который получил Нобелевскую премию за открытие структуры ДНК). Крик (Crick) утверждал, что «очень сложно предположить научную проблему, которая не будет решена за следующие 20 лет … кроме модели работы мозга и процесса самоорганизации белка". Хотя Крик был более заинтересован в функциях мозга, он отметил обе проблемы, потому что они являются сложными из-за того, что в них участвует масса взаимодействий в трехмерном пространстве.
(Levitt M, “Through the breach.” Curr. Opin. Struct. Biol. 1996, 1, 193-194)

Молекулярная Динамика (MD)
В модели молекулярной динамики, мы имитируем движение атомов как функцию от времени на основе уравнений движений Ньютона. Уравнение для системы из N атомов выглядит так
Где, ri и mi это положение и масса атома i , а Fi(t) это функция силы на атом i по времени t. Fi(t) описывается так:
где V（r1, r2, …, rN) потенциальная энергия системы, которая зависит от положения N атомов в системе. ∇i это
(1)
(3)
(2)

Интегрирование с использованием метода конечной разности
Положения в моменты времени (t + Δt ) и (t − Δt ) могут быть выражены через формулы Тэйлора для момента времени t ,
Сумма двух выражений:
Используя формулу (1), получаем:
Мы должны последовательно рассчитывать по формуле (6), чтобы получить траектории атомов в системе. (алгоритм Верлета).
(4a)
(4b)
(6)
(5)

Силы, участвующие в процессе самоорганизации белковой молекулы
Электростатические взаимодействия
Силы Ван дер Ваальса
Водородные связи
Гидрофобные взаимодействия
(Гидрофобные молекулы в водном растворе соединяются друг с другом, так как молекулы воды их отталкивают. Это как разделение в слое масло/вода. Присутствие воды для этих взаимодействий является важным фактором.)

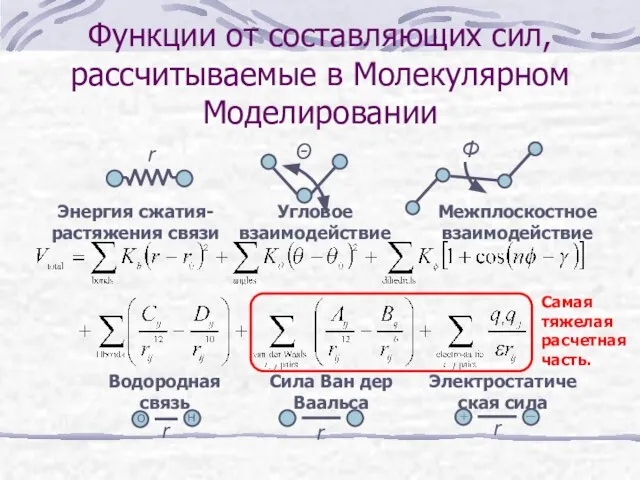
Функции от составляющих сил, рассчитываемые в Молекулярном Моделировании
Электростатическая сила
Водородная связь
Сила Ван дер Ваальса
Энергия сжатия-растяжения связи
Межплоскостное взаимодействие
Угловое взаимодействие
r
Φ
Θ
r
r
r
Самая тяжелая расчетная часть.

Система для Моделирования с помощью Молекулярной Динамики
Без молекул воды
С молекулами воды
Кол-во атомов: 304
Кол-во атомов: 304 + 7,377 = 7,681

MD требует колоссальных вычислительных мощностей
Квант времени в методе MD (Δt) ограничен 1 фсек (10-15 сек).
← Размер Δt должен составлять приблизительно одну десятую от длительности самого быстрого изменения в системе. При моделировании белков, самое быстрое изменение, это изменение энергии сжатия-растяжения связи у легких атомов (например. O-H, C-H), и время этого изменения составляет примерно 10-14 сек, поэтому Δt обычно берется около 1 фсек.
При биомолекулярном MD моделировании должно учитываться большое количество молекул воды.
← Количество атомных пар, учитываемых в расчетах взаимодействий (не считая химические связи, а только силы Ван дер Ваальса и электростатические силы) увеличивается по формуле N 2 (где N это количество атомов).
Сложно моделировать длительный процесс. Обычно, выполняется расчет на несколько десятков наносекунд.

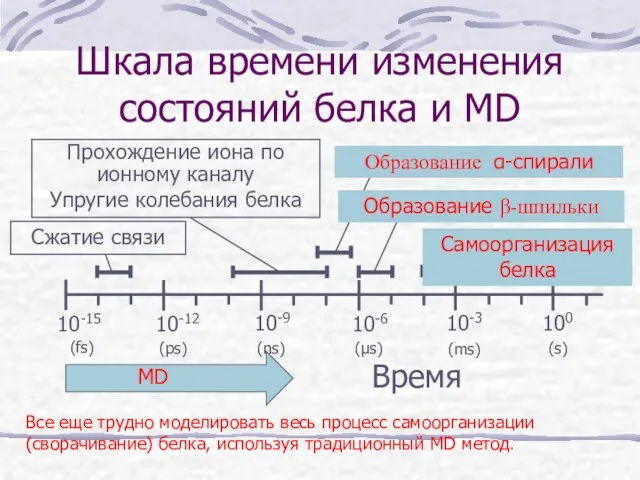
Шкала времени изменения состояний белка и MD
Время
Сжатие связи
Прохождение иона по ионному каналу
Упругие колебания белка
Все еще трудно моделировать весь процесс самоорганизации (сворачивание) белка, используя традиционный MD метод.
Образование α-спирали
Образование β-шпильки
Самоорганизация белка

Гораздо быстрее, Гораздо больше!
Специальные компьютеры
Расчет свободных взаимодействий (не химических связей) обеспечивается с использованием специальных процессоров, разработанных для этих целей.
Например;
MDM (Машина Молекулярной Динамики) или MD-Grape: RIKEN
MD Engine: Taisho Pharmaceutical Co., and Fuji Xerox Co.
Распараллеливание
Задача делится на несколько подзадачей и они обрабатываются каждая на своем процессоре. Сегодня, почти все MD программы для биомолекулярного моделирования (например: AMBER, CHARMm, GROMOS, NAMD, MARBLE, и т.д.) могут работать на параллельных машинах.

Броуновская Динамика (BD)
Динамический вклад растворителя представлен в виде рассеянного случайного воздействия (Открытие Эйнштейна в 1905). Поэтому, молекулы воды могут не рассчитываться как каждая.
С того момента как был создан BD алгоритм, с учетом того, что растворителя гораздо больше и эта энергия сглаживается за очень короткое время, стали возможны расчеты более длинных временных периодов.
BD метод является более подходящим для продолжительного моделирования.

Система для BD Моделирования
Без молекул воды
С молекулами воды
Кол-во атомов: 304
Кол-во атомов: 304 + 7,377 = 7,681

Алгоритм BD
Уравнение Ланжевина может быть выражено так:
Здесь, ri и mi отражают соответственно положение и массу атома i. ζi это коэффициент трения, определяемый законом Стокса., то есть ζi = 6πaiStokesη, где aiStokes это Стоксовский радиус атома i , а η это вязкость воды. Fi это систематическое воздействие на атом i. Ri случайное воздействие на атом i , равное 0
= 0 , а вариации
= 6ζikTδijδ(t); это выводится из свойств растворителя.
Для задемпфированного предела, левую часть уравнения (7) мы приравниваем 0,
Интегрированное выражение уравнения 8 называется Броуновская Динамика;
где Δt это шаг времени, а ωi это случайный вектор помех, получающийся из распределения Гаусса.
(7)
(9)
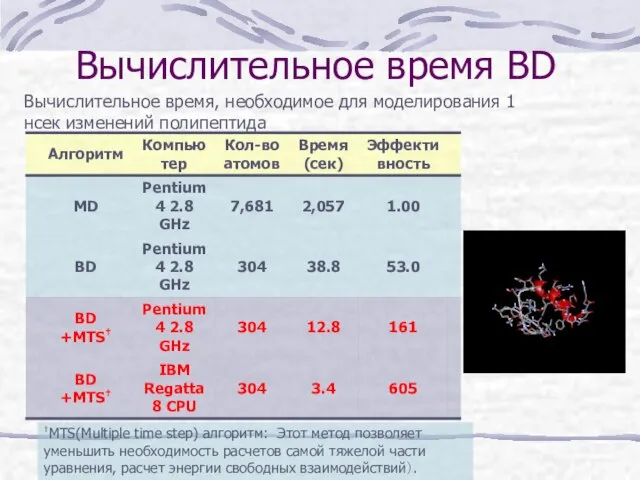
(8)

Вычислительное время BD
†MTS(Multiple time step) алгоритм: Этот метод позволяет уменьшить необходимость расчетов самой тяжелой части уравнения, расчет энергии свободных взаимодействий）.
Вычислительное время, необходимое для моделирования 1 нсек изменений полипептида

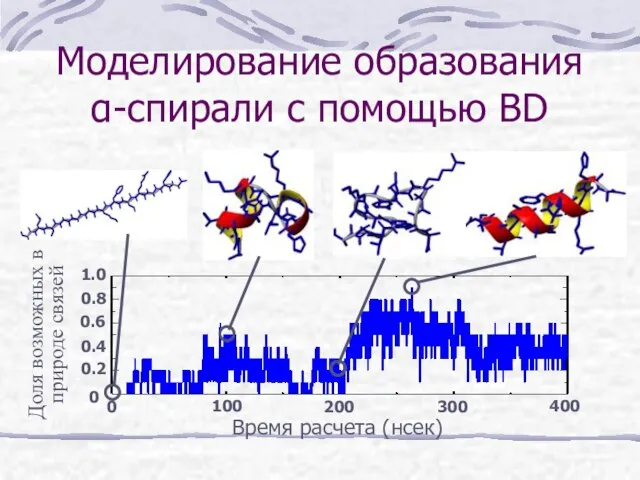
Моделирование образования α-спирали с помощью BD
Доля возможных в природе связей
Время расчета (нсек)
0
300
200
100
400
0
0.2
0.4
0.6
0.8
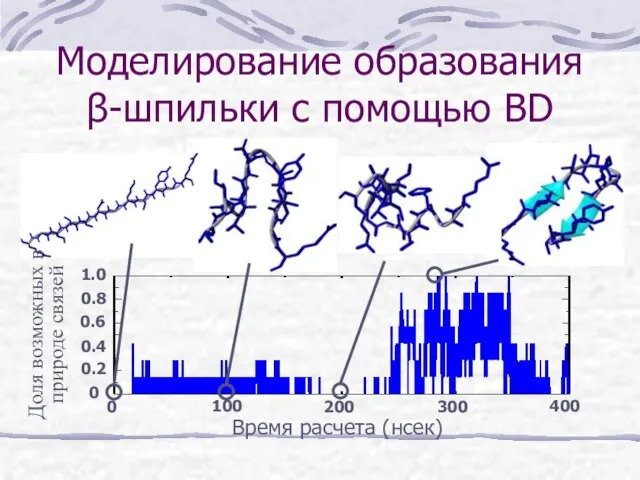
1.0

Моделирование образования
β-шпильки с помощью BD
Доля возможных в природе связей
Время расчета (нсек)
0
300
200
100
400
0
0.2
0.4
0.6
0.8
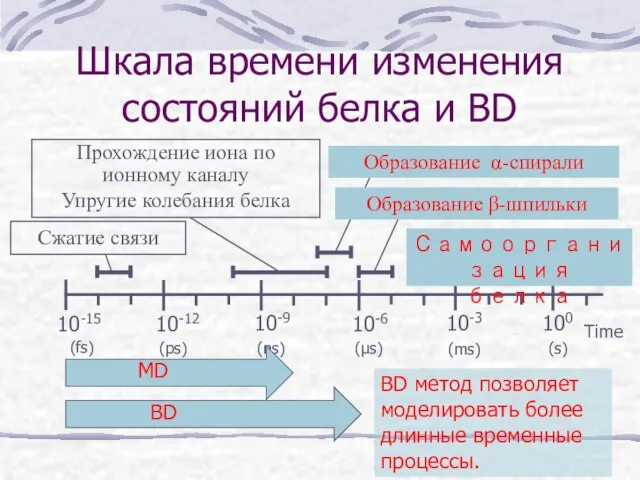
1.0

Шкала времени изменения состояний белка и BD
Time
BD метод позволяет моделировать более длинные временные процессы.
Образование α-спирали
Образование β-шпильки
Самоорганизация белка
MD
Сжатие связи
Прохождение иона по ионному каналу
Упругие колебания белка