Введение в теорию графов

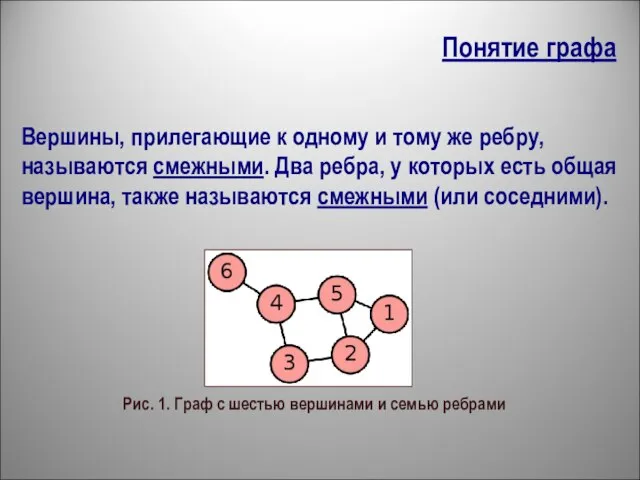
Граф отображает элементный состав системы и структуру связей.
Граф - это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек.
Понятие графа

Вершины, прилегающие к одному и тому же ребру, называются смежными. Два ребра, у которых есть общая вершина, также называются смежными (или соседними).
Рис. 1. Граф с шестью вершинами и семью ребрами
Понятие графа

Петля - это дуга, начальная и конечная вершина которой совпадают.
Пустым (нулевым) называется граф без ребер.
Полным называется граф, в котором каждые две вершины смежные.
Элементы графа

Нулевой граф
Граф, состоящий из «изолированных» вершин, называется нулевым графом
Рис. 2. Нулевой граф

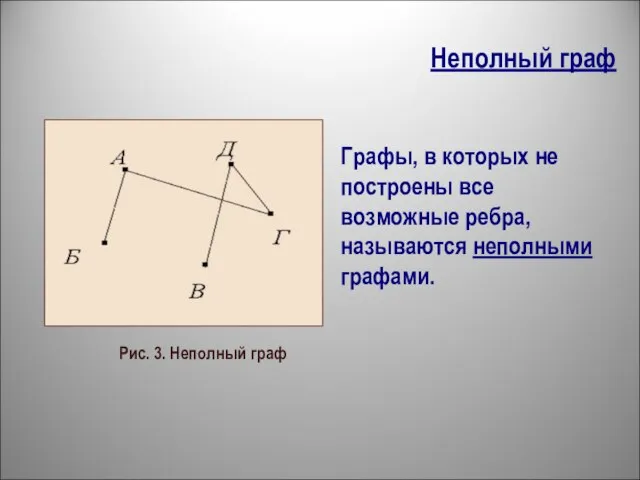
Неполный граф
Графы, в которых не построены все возможные ребра, называются неполными графами.
Рис. 3. Неполный граф

Степень графа
Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной.
Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный.

Если граф полный и имеет n вершин, то количество его ребер равно n(n-1)/2
Задание 1. Существует ли полный граф с семью ребрами?
Решение: Зная количество ребер, узнаем количество вершин.
n(n-1)/2=7.
n(n-1)=14.
n и (n-1) – это два последовательных натуральных числа. Число 14 нельзя представить в виде произведения двух последовательных натуральных чисел, значит, данное уравнение не имеет решений. Следовательно, такого графа
не существует.
ОТВЕТ

Построить полный граф, если известно что он содержит в себе 7 вершин.
Составьте схему проведения розыгрыша кубка по олимпийской системе, в которой участвуют 10 команд.
Задание 2.

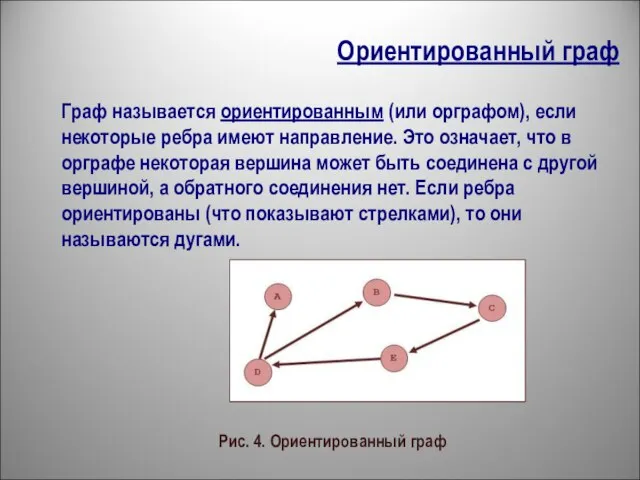
Ориентированный граф
Граф называется ориентированным (или орграфом), если некоторые ребра имеют направление. Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Если ребра ориентированы (что показывают стрелками), то они называются дугами.
Рис. 4. Ориентированный граф

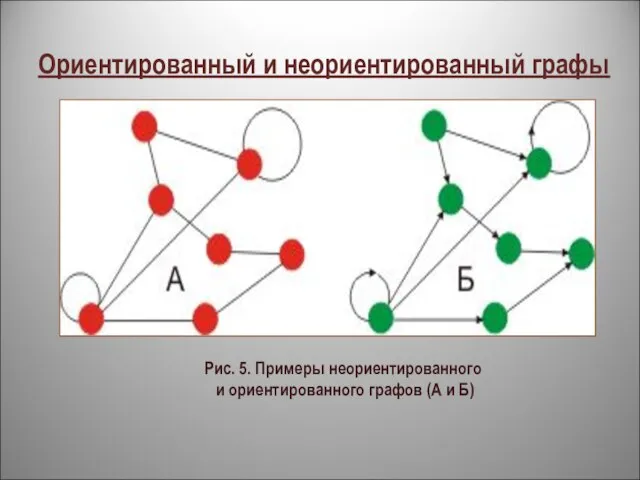
Рис. 5. Примеры неориентированного
и ориентированного графов (А и Б)
Ориентированный и неориентированный графы

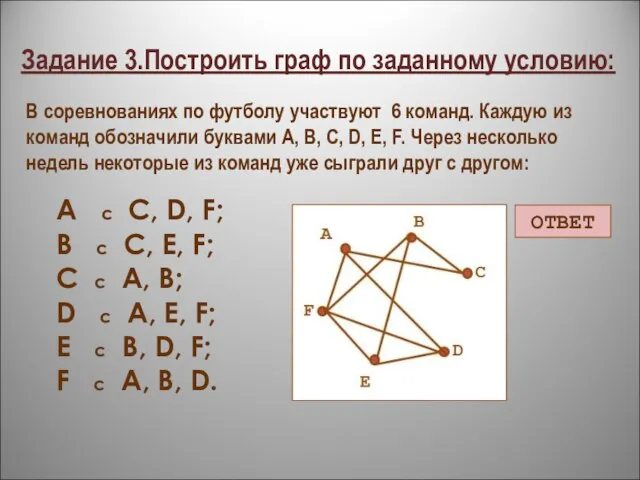
Задание 3.Построить граф по заданному условию:
В соревнованиях по футболу участвуют 6 команд. Каждую из команд обозначили буквами А, B, C, D, E, F. Через несколько недель некоторые из команд уже сыграли друг с другом:
A с C, D, F;
B c C, E, F;
С с A, B;
D с A, E, F;
E с B, D, F;
F с A, B, D.
ОТВЕТ

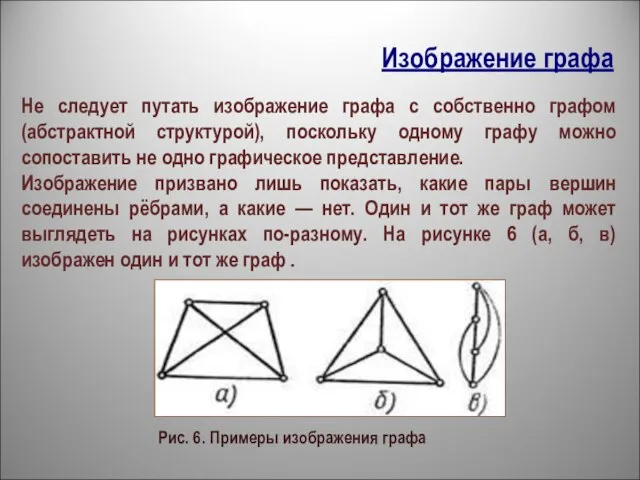
Изображение графа
Рис. 6. Примеры изображения графа
Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление.
Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Один и тот же граф может выглядеть на рисунках по-разному. На рисунке 6 (а, б, в) изображен один и тот же граф.

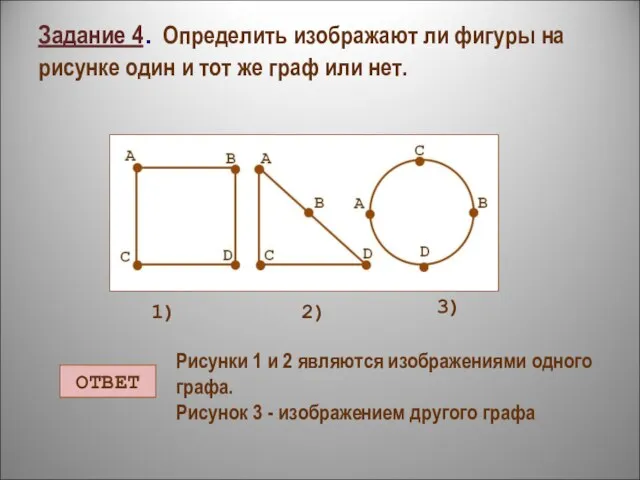
Задание 4. Определить изображают ли фигуры на рисунке один и тот же граф или нет.
1)
2)
3)
ОТВЕТ
Рисунки 1 и 2 являются изображениями одного графа.
Рисунок 3 - изображением другого графа

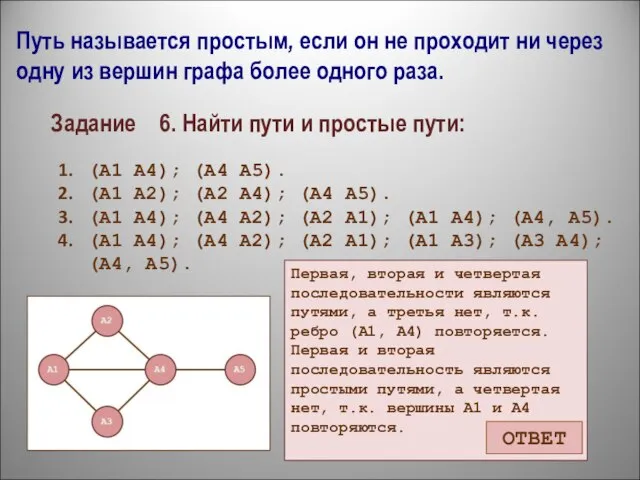
Задание 5. Определить какая из перечисленных последовательностей путём не является.
(А1 А4); (А4 А5).
(А1 А2); (А2 А4); (А4 А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А4); (А4, А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А3); (А3 А4); (А4, А5).
ОТВЕТ
Третья последовательность (А1 А4); (А4 А2); (А2 А1); (А1 А4); (А4, А5).
Путь в графе
Путём в графе называется такая последовательность ребер, в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза.

Путь называется простым, если он не проходит ни через одну из вершин графа более одного раза.
(А1 А4); (А4 А5).
(А1 А2); (А2 А4); (А4 А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А4); (А4, А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А3); (А3 А4); (А4, А5).
Задание 6. Найти пути и простые пути:
Определите, какие последовательности ребер являются путями, и какие из них простые. Если последовательность не является путем укажите почему.
Первая, вторая и четвертая последовательности являются путями, а третья нет, т.к. ребро (А1, А4) повторяется.
Первая и вторая последовательность являются простыми путями, а четвертая нет, т.к. вершины А1 и А4 повторяются.
ОТВЕТ

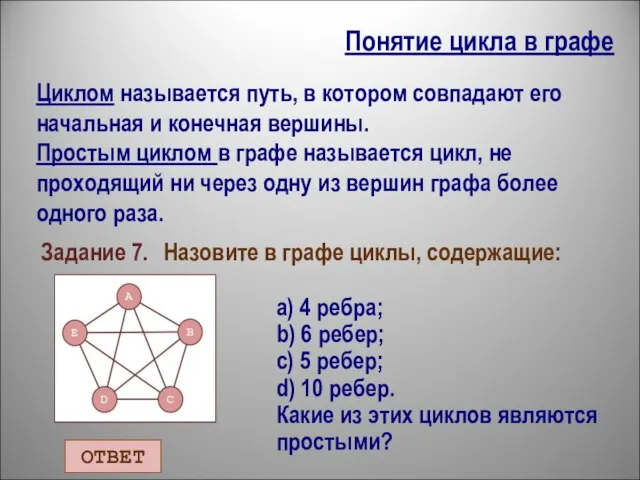
Понятие цикла в графе
Циклом называется путь, в котором совпадают его начальная и конечная вершины.
Простым циклом в графе называется цикл, не проходящий ни через одну из вершин графа более одного раза.
Задание 7. Назовите в графе циклы, содержащие:
a) 4 ребра;
b) 6 ребер;
c) 5 ребер;
d) 10 ребер.
Какие из этих циклов являются простыми?
ОТВЕТ