Выбор пути решения задачи

Проблема выбора пути решения – это одна из важнейших методологических и логических характеристик исследовательского процесса
Следует различать такие пути, такие намерения, идеи, которые ведут к решению с одной стороны и такие, которые оказываются тупиковыми, с другой.
Парадоксальность исследовательского процесса состоит в том, что те и другие активизируют и стимулируют поисковую деятельность, побуждают исследователя к осуществлению тех или иных действий, которые в той или иной степени могут все-таки оказаться продуктивными.

Педагогически неверно давать задачу с требованием решить ее именно таким способом, если возможен иной, более короткий и красивый и не очень замаскированный способ ее решения.

Задача
МГУ. Экономический факультет
Среди решений системы найдите
те, при которых выражение принимает наибольшее значение.

1 решение
Геометрия

Уравнения системы твердо ассоциируются с теоремой Пифагора,
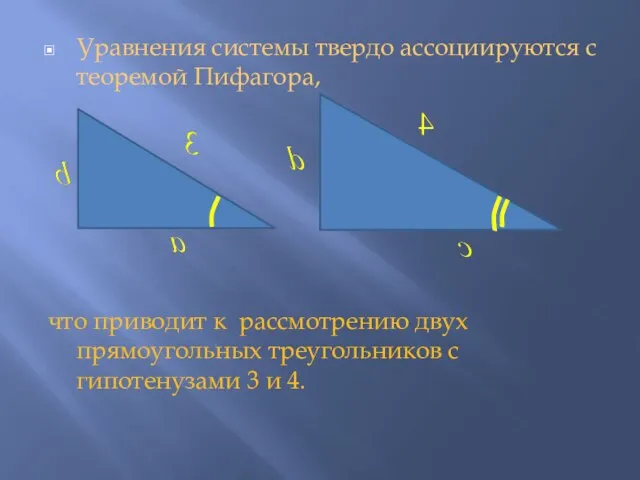
что приводит к рассмотрению двух прямоугольных треугольников с гипотенузами 3 и 4.

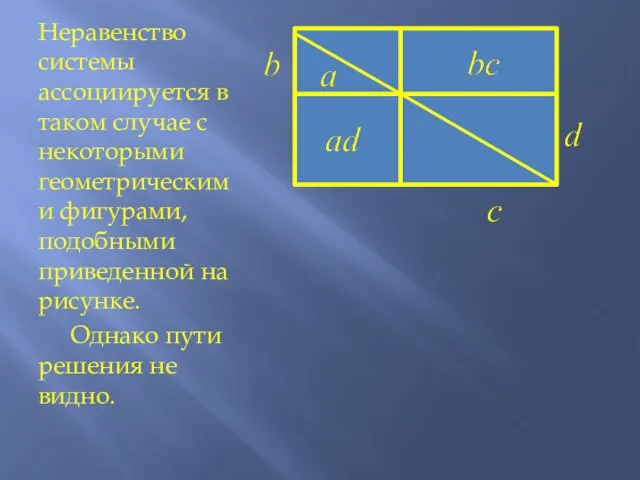
Неравенство системы ассоциируется в таком случае с некоторыми геометрическими фигурами, подобными приведенной на рисунке.
Однако пути решения не видно.

2 решение
Тригонометрия

Введение тригонометрических функций

Учитывая, что , и то, что
получим, что , т.е. рассматриваемые нами треугольники подобны.
Получим, что
и максимальное значение достигается, если
Тогда:

3 решение
Теория чисел.

Теорема и формула Эйлера
Теорема Эйлера.
Произведение двух чисел, каждое из которых есть сумма двух квадратов, также представимо в виде суммы двух квадратов.
Формула Эйлера.

Имеем, что , и , таким
образом, получаем, что
Из уравнений системы получим, что
Последнее выражение достигает максимума при

Подставив найденное значение, получим, что
и одновременно находим искомые значения
К решению задачи нас привел непростой, сложный путь.
Однако после этого вдруг может стать ясно, что к тому же
результату ведет и более короткий путь, но его нахождение
требует гораздо большей знаниевой оснащенности

Размышление о поиске пути решения в яркой форме выразил Г.Гельмгольц:
«Я могу сравнить себя с путником, который
предпринял восхождение на гору, не зная дороги;
долго и с трудом взбирается он, часто должен
возвращаться назад, ибо дальше нет прохода. То
размышление, то случай открывают ему новые
тропинки, они ведут его несколько далее, и, наконец,
когда цель достигнута, он, к своему стыду, находит
широкую дорогу, по которой мог бы подняться, если
бы умел верно отыскать начало»

4 решение
Векторы

Рассмотрим векторы
Система запишется в виде
Но из величины скалярного произведения
имеем, что , откуда следует, что
векторы коллинеарны и сонаправлены.

Отложив векторы от начала координат и обозначив угол, составленный векторами с осью абсцисс , снова получим, что
Как и в предыдущих случаях получим, что