Содержание
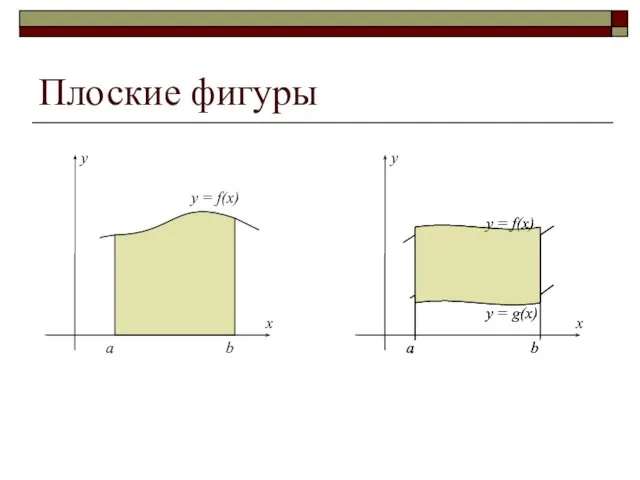
- 2. Плоские фигуры a b y = f(x) a b y = f(x) y = g(x) a
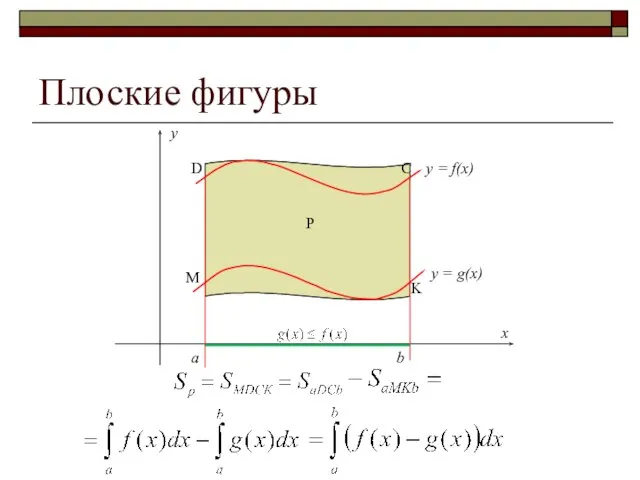
- 3. y = g(x) a b y = f(x) Плоские фигуры Р M K C D
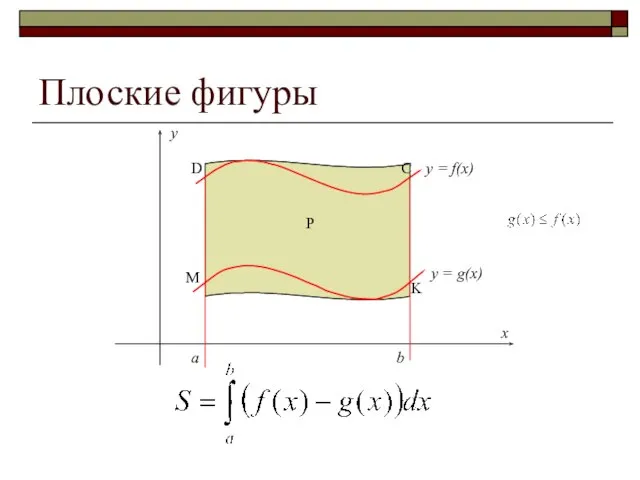
- 4. y = g(x) a b y = f(x) Плоские фигуры Р M K C D
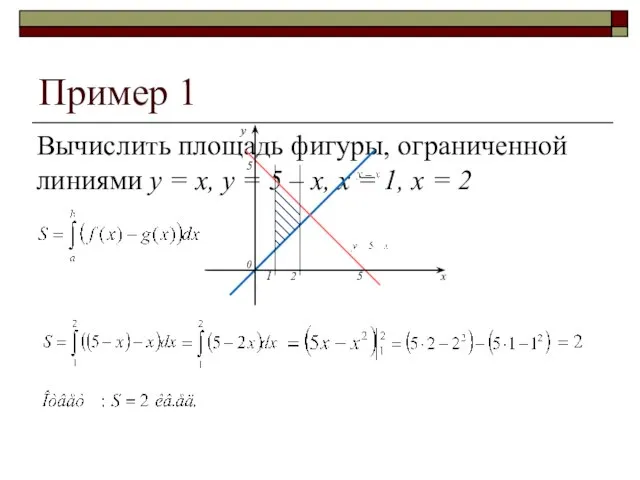
- 5. Пример 1 Вычислить площадь фигуры, ограниченной линиями y = x, y = 5 – x, x
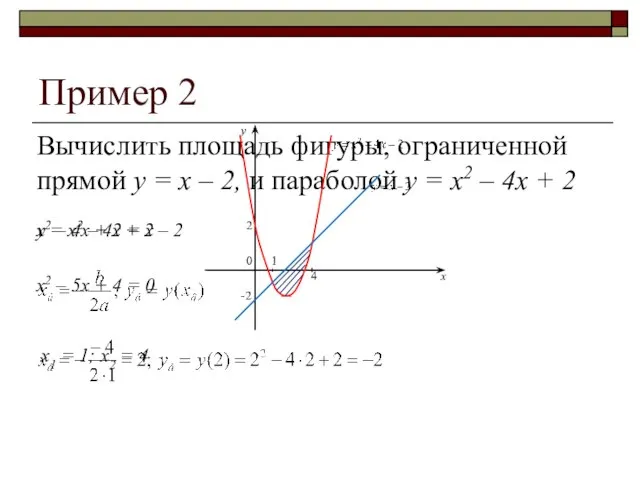
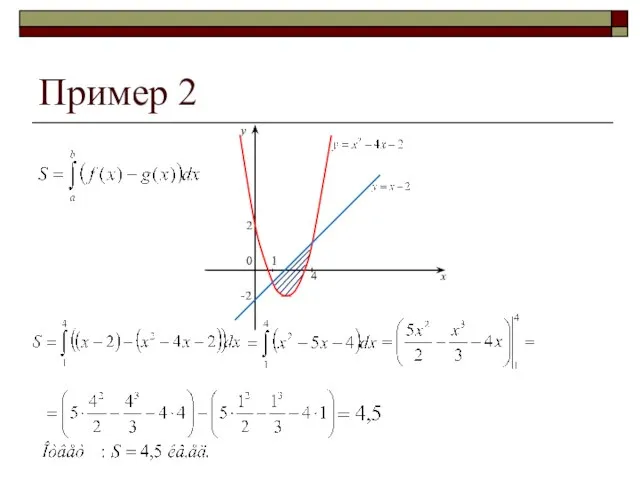
- 6. Пример 2 Вычислить площадь фигуры, ограниченной прямой y = x – 2, и параболой y =
- 7. Пример 2 2 0 -2 1 4
- 8. Задание 1 Вычислите площадь фигуры, ограниченной прямыми: а) y = x, y = -0,5x + 5,
- 9. Задание 2 Вычислите площадь фигуры, ограниченной графиками функций: а) y = 1 – x2, y =
- 11. Скачать презентацию


 Презентация на тему Итоговое сочинение по литературе
Презентация на тему Итоговое сочинение по литературе Speaking about the past
Speaking about the past Было ли предательством избрание на престол Владислава?
Было ли предательством избрание на престол Владислава? Презентация на тему Развивающие задачи для 5-6 классов
Презентация на тему Развивающие задачи для 5-6 классов НИРС. Портфолио
НИРС. Портфолио МБОУ "Верхопенская СОШ им. М.Р. Абросимова"
МБОУ "Верхопенская СОШ им. М.Р. Абросимова" Мероприятие по экологии«День Земли»
Мероприятие по экологии«День Земли» Межшкольные курсыпо подготовке колимпиаде школьников
Межшкольные курсыпо подготовке колимпиаде школьников Проект Красная книга или возьмём под защиту
Проект Красная книга или возьмём под защиту КРУ серии К-129 ПС 110/10 кВ «Петровщина» ОАО «Минскэнерго»
КРУ серии К-129 ПС 110/10 кВ «Петровщина» ОАО «Минскэнерго» Презентация на тему: ПИСЬМО ПО ПАМЯТИ Автоматизация свистящих звуков
Презентация на тему: ПИСЬМО ПО ПАМЯТИ Автоматизация свистящих звуков Аренда Элитного Жилья
Аренда Элитного Жилья ЕЛЕЦКОЕ
ЕЛЕЦКОЕ Школьные службы примирения:
Школьные службы примирения: «ПРАВИЛА ДВУХ СТИВЕНОВ»
«ПРАВИЛА ДВУХ СТИВЕНОВ» Государственная служба Российской Федерации
Государственная служба Российской Федерации Презентація 014
Презентація 014 День рождения Медведя
День рождения Медведя Tuberculosis Disease
Tuberculosis Disease Взаимосвязанное обучение языку и культуре как основа формирования способности к межкультурной коммуникации
Взаимосвязанное обучение языку и культуре как основа формирования способности к межкультурной коммуникации Астрент как правовой институт
Астрент как правовой институт Деятельность Этнокультурных центров на территории Пряжинского национального муниципального района
Деятельность Этнокультурных центров на территории Пряжинского национального муниципального района Cell Injury, Cell Death, and Adaptations
Cell Injury, Cell Death, and Adaptations  Электромеханические аппараты управления ЭП
Электромеханические аппараты управления ЭП Проект. КОНТРОЛЬ И ДИАГНОСТИКА СОСТОЯНИЯ НАГРУЗКИ В ЭЛЕКТРООБОРУДОВАНИИ ТРАНСПОРТНЫХ СРЕДСТВ Алексеев Виталий Альбертович Конта
Проект. КОНТРОЛЬ И ДИАГНОСТИКА СОСТОЯНИЯ НАГРУЗКИ В ЭЛЕКТРООБОРУДОВАНИИ ТРАНСПОРТНЫХ СРЕДСТВ Алексеев Виталий Альбертович Конта Презентация на тему Как появилась наша Земля
Презентация на тему Как появилась наша Земля Сертификация газонефтепроводов и газонефтехранилищ
Сертификация газонефтепроводов и газонефтехранилищ Тайна как инструмент изучения бессознательного в культурно-историческом подходе
Тайна как инструмент изучения бессознательного в культурно-историческом подходе