Вычислительный аспект задач построения трендов

Большаков М.А.
Вычислительный аспект задач построения трендов
Основные определения
ПРОГНОЗ - (forecast, prognosis, от греч. prognosis- предузнавание, предвидение, предсказание) - предвидение, предсказание хода какого-либо процесса, будущего состояния какого-либо явления.
ПРОГНОЗИРОВАНИЕ - разработка прогноза; в узком значении - специальные научные исследования конкретных перспектив развития какого-либо явления. Как одна из форм конкретизации научного предвидения в социальной сфере находится во взаимосвязи с планированием, программированием, проектированием, управлением. Обычно в общественных науках: краткосрочное прогнозирование на 1-2 года, среднесрочное на 5-10 лет, долгосрочное на 15-20 лет, сверхдолгосрочное на 50-100 лет. Выделяют три класса методов прогнозирования: экстраполяция, моделирование, опрос экспертов.
ТРЕНД - тенденция изменения экономических показателей.
Все определения взяты из словаря «Финанасовый менеджмент» серии Economicus

Большаков М.А.
Вычислительный аспект задач построения трендов
Модели временных рядов
Статистические методы исследования исходят из предположения о возможности представления значений временного ряда в виде суммы нескольких компонент, отражающих закономерность и случайность развития, в частности в виде суммы трех компонент:
Y(t) = T(t) + S(t) + E(t), где
T(t) - тренд (долговременная тенденция) развития;
S(t) - сезонная компонента;
E(t) - остаточная компонента.
Сезонная компонента характеризует устойчивые внутригодичные колебания уровней.

Большаков М.А.
Вычислительный аспект задач построения трендов
Классификация процессов
процессы без «предела роста»
процессы с «пределом роста»
процессы с «пределом роста» и «точкой перегиба»

Большаков М.А.
Вычислительный аспект задач построения трендов
Модели кривых роста (1 тип)

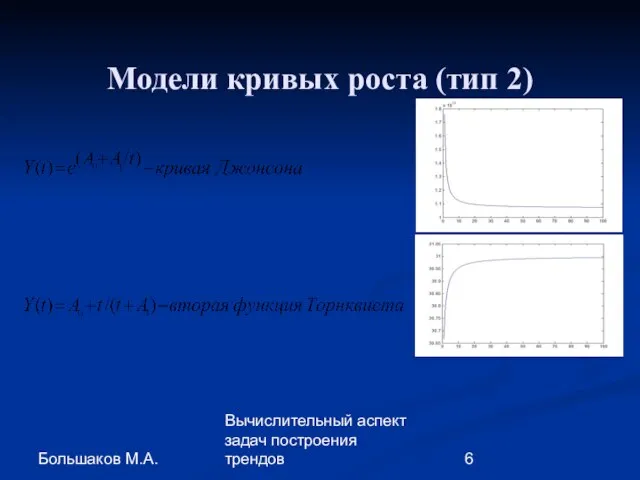
Большаков М.А.
Вычислительный аспект задач построения трендов
Модели кривых роста (тип 2)

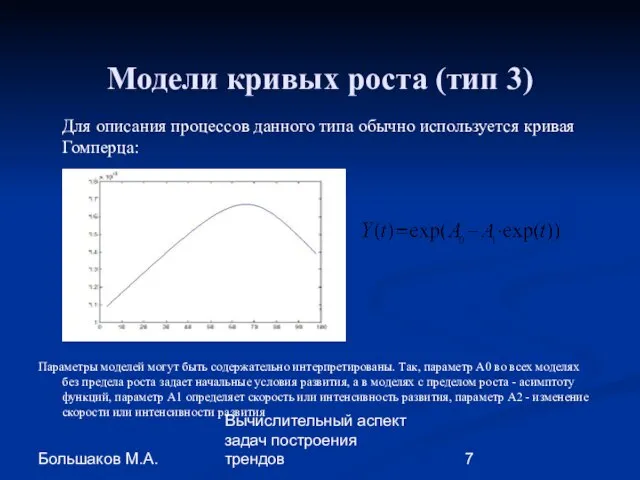
Большаков М.А.
Вычислительный аспект задач построения трендов
Модели кривых роста (тип 3)
Для описания процессов данного типа обычно используется кривая Гомперца:
Параметры моделей могут быть содержательно интерпретированы. Так, параметр А0 во всех моделях без предела роста задает начальные условия развития, а в моделях с пределом роста - асимптоту функций, параметр А1 определяет скорость или интенсивность развития, параметр А2 - изменение скорости или интенсивности развития

Большаков М.А.
Вычислительный аспект задач построения трендов
Адаптивные модели прогнозирования
Для лучшего отображения особенностей изменения исследуемого показателя на конце периода наблюдения целесообразно использовать адаптивные модели, каждая из которых имеет определенный механизм приспособления к новым условиям. Общим для всех моделей этой группы является придание наибольшего веса последним наблюдениям при оценке параметров.

Большаков М.А.
Вычислительный аспект задач построения трендов
Схема скользящего среднего
В практике статистического прогнозирования наиболее часто используются две базовые СС-модели: Брауна и Хольта, первая из которых является частным случаем второй. Эти модели представляют процесс развития как линейную тенденцию с постоянно изменяющимися параметрами.
Прогнозная оценка Yp(t,k) уровня ряда Y(t+k), вычисляются в момент времени t на k шагов вперед:
Yp(t,k) = A0(t) + A1(t)* k, (1),где
A0(t) - оценка текущего (t-го) уровня;
A1(t) - оценка текущего прироста.
Далее определяется величина их расхождения (ошибки). При k=1 имеем:
e(t+1) = Y(t+1) - Yp(t,1). В соответствии с этой величиной корректируются параметры модели

Большаков М.А.
Вычислительный аспект задач построения трендов
Модель Брауна
A0(t) = A0(t-1) + A1(t-1) + (1- b ^2)* e(t);
A1(t) = A1(t-1) + (1- b )^2*e(t); где
b - коэффициент дисконтирования данных, изменяющийся в пределах от 0 до 1;
a - коэффициент сглаживания (a = 1 - b );
е(t) - ошибка прогнозирования уровня Y(t), вычисленная в момент времени (t-1) на один шаг вперед

Большаков М.А.
Вычислительный аспект задач построения трендов
Модель Хольта
A0(t) = A0(t-1) + A1(t-1) + a 1* e(t);
A1(t) = A1(t-1) +a 1* a 2* e(t); где
a 1,a 2 - коэффициенты сглаживания (адаптации), изменяющиеся в пределах от 0 до 1.
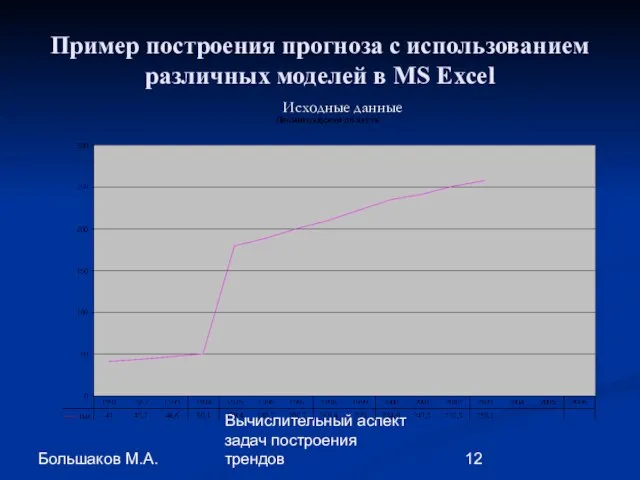
е(t) - ошибка прогнозирования уровня Y(t), вычисленная в момент времени (t-1) на один шаг вперед

Большаков М.А.
Вычислительный аспект задач построения трендов
Пример построения прогноза с использованием различных моделей в MS Excel
Исходные данные

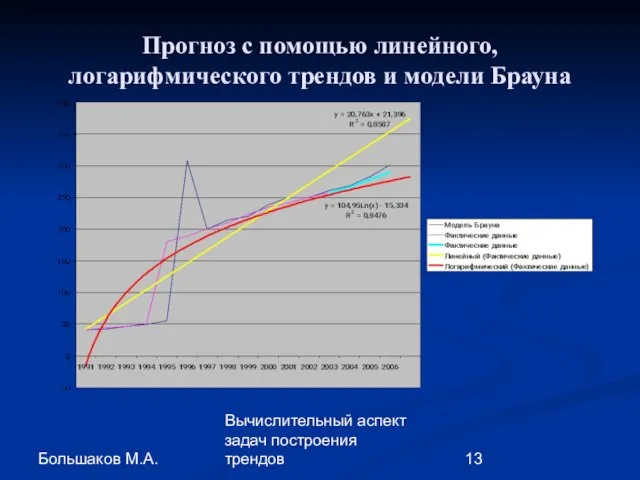
Большаков М.А.
Вычислительный аспект задач построения трендов
Прогноз с помощью линейного, логарифмического трендов и модели Брауна

Большаков М.А.
Вычислительный аспект задач построения трендов
Наиболее популярные пакеты, применяемые в области построения прогнозов
Автоматизированная система прогнозирования временных рядов «Adviser»
Система
"Трендовые методы прогнозирования"
SPSS Advanced Models
SPSS Trends
spellabs time series и др.