Содержание
- 2. Цели урока Цели: Рассмотреть разные случаи взаимного расположения графиков линейных функций. Научились распознавать взаимное расположение графиков
- 3. Экспресс – опрос: Какую функцию называют линейной? Что является графиком линейной функции? Какой формулой задаётся прямая
- 5. Исследование графиков линейных функций. Заполните таблицы для построения графиков функций. 1 вариант 2 вариант 1) у=2х+4
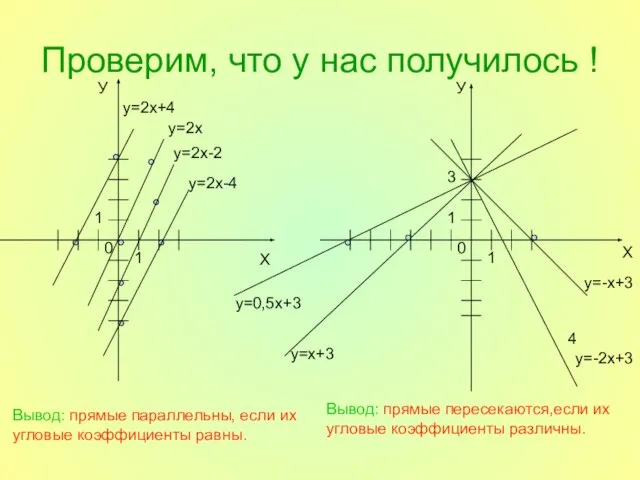
- 6. Проверим, что у нас получилось ! У Х у=2х+4 у=2х у=2х-2 у=2х-4 У Х 4 у=-х+3
- 7. Ось абсцисс. Раз. Два. Подтянулись. Ось ординат. Подтянулись. Прямая .y=kx+b. K – положительное. Наклон вправо. Подтянулись.
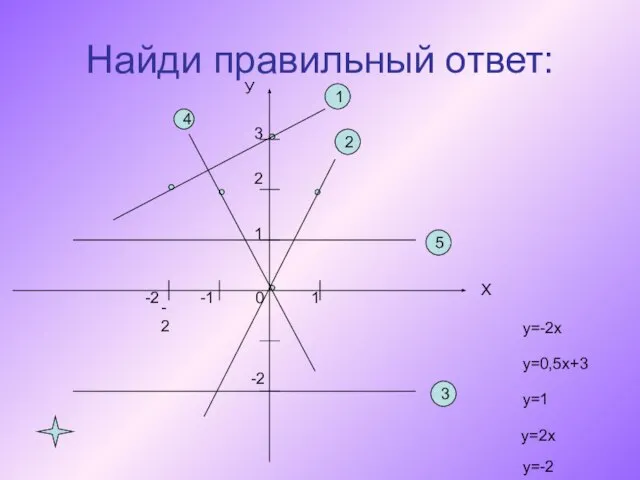
- 8. Найди правильный ответ: У Х 3 1 1 -2 -2 5 -2 3 2 2 1
- 9. Правильно! Это прямые у =0,5х+3 и у = -2х А вот ещё несколько примеров :
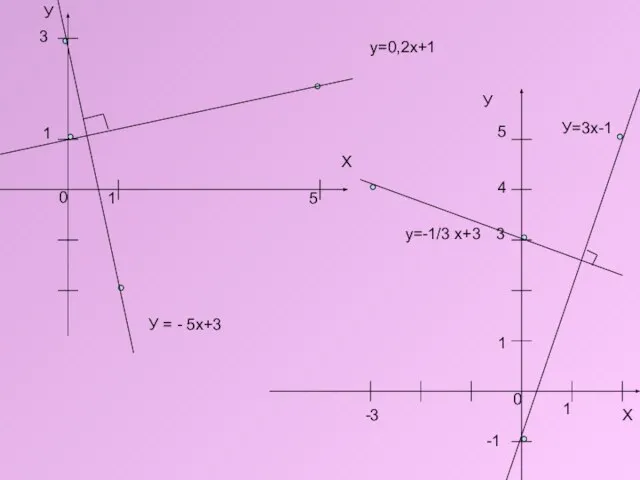
- 10. У Х 1 5 3 1 у=0,2х+1 У = - 5х+3 У Х 3 -1 -3
- 11. ВНИМАТЕЛЬНО ПОСМОТРИТЕ НА УРАВНЕНИЯ ПЕРПЕНДИКУЛЯРНЫХ ПРЯМЫХ И ПОПРОБУЙТЕ ОТВЕТИТЬ НА ВОПРОС: При каком условии две прямые
- 12. Первая подсказка: Обратите внимание на угловые коэффициенты: 0,5 и - 2 - 5 и 0,2 3
- 13. Так когда же две прямые перпендикулярны ? Вывод : две прямые перпендикулярны , если произведение их
- 14. Давайте теперь оформим результаты всех наших исследований и уточним … За что же «отвечает» угловой коэффициент
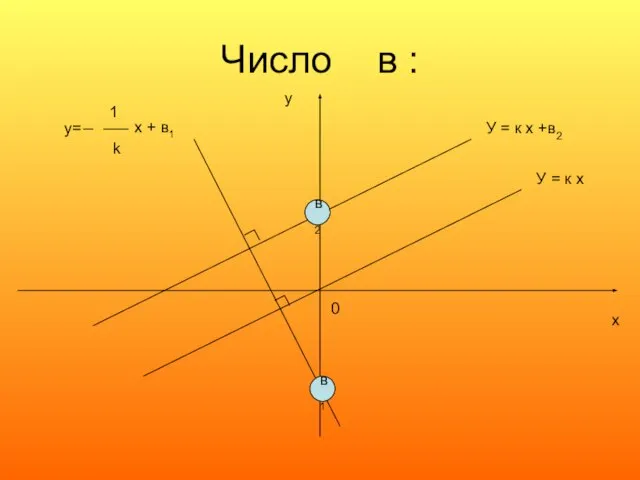
- 15. Число k:
- 16. Число в : у х 0 У = к х У = к х +в2 в2
- 17. Самостоятельная работа . Даны две линейных функции y=k1x+b1и y = k2x+ b2 Подберите такие координаты k1,
- 19. Скачать презентацию












 Почтовая открытка 23 февраля
Почтовая открытка 23 февраля Изомерия. Классификация органических веществ.
Изомерия. Классификация органических веществ. Обыкновенные дроби (5 класс)
Обыкновенные дроби (5 класс) Проектно- исследовательская деятельность младших школьников
Проектно- исследовательская деятельность младших школьников Стили речи. Введение в стилистику
Стили речи. Введение в стилистику Конкурс как способ организации досугового мероприятия
Конкурс как способ организации досугового мероприятия 1. Oppitunti (2)
1. Oppitunti (2) Разработка рекламных мероприятий по продвижению компании «Горячие туры» в социальных сетях Дипломный проект Рябиги О.С Группа Р
Разработка рекламных мероприятий по продвижению компании «Горячие туры» в социальных сетях Дипломный проект Рябиги О.С Группа Р 20141105_voronezh_segodnya
20141105_voronezh_segodnya Экосистема. Структура экосистемы
Экосистема. Структура экосистемы Славяне в древности
Славяне в древности 29.11.2011г.Студенты группы Ф -22 совместно с кураторомпосетили
29.11.2011г.Студенты группы Ф -22 совместно с кураторомпосетили Презентация 3
Презентация 3 9 «В» Февраль 2012
9 «В» Февраль 2012 дата проведения: 11.01.10Провела:Учитель информатики и ВТХрусцелевская Н.В.Прослушал:5 класс
дата проведения: 11.01.10Провела:Учитель информатики и ВТХрусцелевская Н.В.Прослушал:5 класс Тема: «Великий художник природы – вода».
Тема: «Великий художник природы – вода». Vox – Технология будущего
Vox – Технология будущего Architecture Styles in America
Architecture Styles in America  План проведения педагогического совета 1. Вступление. Анализ выполнения решений предыдущего педагогического совета. 2. Доклад «Сти
План проведения педагогического совета 1. Вступление. Анализ выполнения решений предыдущего педагогического совета. 2. Доклад «Сти Загадочная смерть Маяковского
Загадочная смерть Маяковского Учебное исследование и проектная работа. Основные понятия
Учебное исследование и проектная работа. Основные понятия ЯПОНИЯ
ЯПОНИЯ Характеристика и особенности оформления справок, докладных и объяснительных записок
Характеристика и особенности оформления справок, докладных и объяснительных записок Религиозная толерантность
Религиозная толерантность Презентация на тему Динамика материальной точки. Работа и энергия
Презентация на тему Динамика материальной точки. Работа и энергия
 IT Construct ООО «Ай Ти Констракт»
IT Construct ООО «Ай Ти Констракт» РАЗРАБОТКА И ВНЕДРЕНИЕ УЧЕБНИКОВ ПО БАЙКАЛОВЕДЕНИЮ В ШКОЛЬНОЕ ОБРАЗОВАНИЕ БАЙКАЛЬСКОГО РЕГИОНА
РАЗРАБОТКА И ВНЕДРЕНИЕ УЧЕБНИКОВ ПО БАЙКАЛОВЕДЕНИЮ В ШКОЛЬНОЕ ОБРАЗОВАНИЕ БАЙКАЛЬСКОГО РЕГИОНА Верховный суд США
Верховный суд США