Взаимное расположение графиков линейных функций

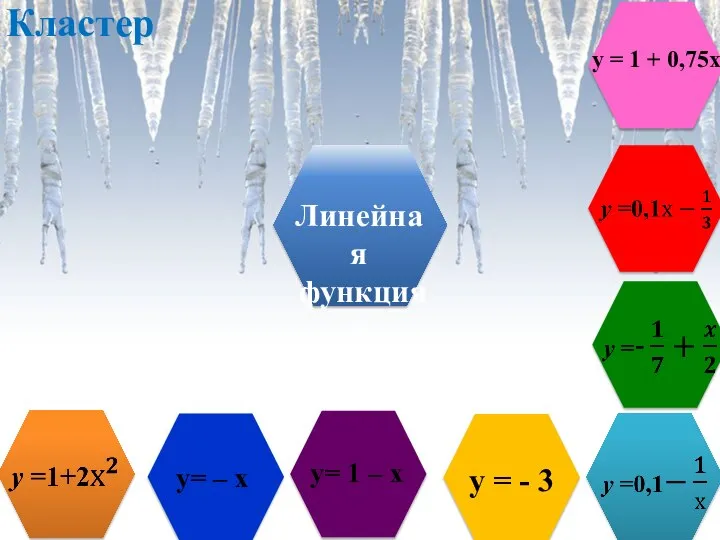
Кластер
у= – х

Вариант 1
Постройте график функции, заданной формулой
у = –2х+ 0,5.
2. Линейная функция задана формулой у = 5х – 12. Найдите:
а) значение у, если х = 1,2; –3;
б) значение х, при котором у = 0; –1,5.
Вариант 2
1. Постройте график функции, заданной формулой у = –3х– 1,5.
2. Линейная функция задана формулой у = –4х + 7. Найдите:
а) значение у, если х = –1,3; 8;
б) значение х, при котором у = –2,8; 0.
Самостоятельная работа.

Т е с т

1. Функция задана формулой у = 2х – 15. Определите:
а) значение у, если х = –3,5;
б) значение х, при котором у = –5;
в)проходит ли график функции через точку K (10;5).
Упражнения

1. у = 2х – 15.
а) Если х = –3,5, то у = 2 • (–3,5) – 15 =
= –7 – 15 = –22;
б) если у = –5, то 2х – 15 = –5;
2х = –5 + 15;
2х = 10;
х = 5;
в) –5 = 2 • 10 – 15;
–5 = 20 – 15;
–5 = 5 – неверно, значит, график функции не проходит через точку
K (10; –5).
Ответ: а) –22; б) 5; в) не проходит.
Решение

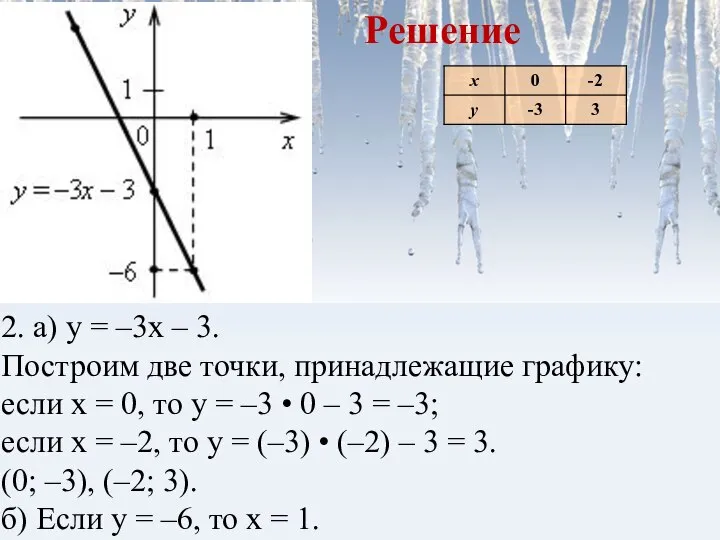
2. а) Постройте график функции у = –3х – 3.
б) Укажите с помощью графика, при каком значении х значение у равно 3 .
Упражнения

2. а) у = –3х – 3.
Построим две точки, принадлежащие графику:
если х = 0, то у = –3 • 0 – 3 = –3;
если х = –2, то у = (–3) • (–2) – 3 = 3.
(0; –3), (–2; 3).
б) Если у = –6, то х = 1.
Решение

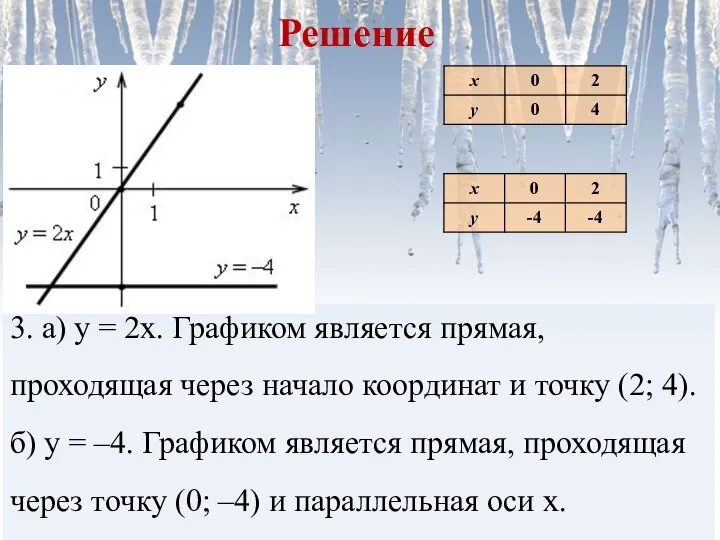
3. В одной и той же системе координат постройте график функций:
а) у = 2х; б) у = –4.
Упражнения

Решение
3. а) у = 2х. Графиком является прямая, проходящая через начало координат и точку (2; 4).
б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.

4. Найдите координаты точки пересечения графиков функций
у = –10х – 9 и у = –24х + 19.
Упражнения

4. Решим уравнение:
–10х – 9 = –24х + 19;
–10х + 24х = 19 + 9;
14х = 28;
х = 28 : 14;
х = 2, значит, абсцисса точки пересечения графиков равна 2. Найдем соответствующее значение ординаты:
если х = 2, то у = –10 • 2 – 9 = –29.
Точка пересечения имеет координаты (2; –29).
Ответ: (2; –29).
Решение

5. Задайте формулой линейную функцию, график которой параллелен прямой у = –8х + 11 и проходит через начало координат.
Упражнения

5. График параллелен прямой у = –8х + 11, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это – прямая пропорциональность. Значит, у = –8х.
Ответ: у = –8х.
Решение

Задание на самоподготовку.
п. 15, п. 16. № 360; № 363; № 372.