Содержание
- 2. Признаки делимости натуральных чисел известные уже с 6 класса, например, признаки делимости на 2, на 3,
- 3. При решении задач на делимость часто бывают полезными свойства, связанные с последовательным расположением целых чисел Одно
- 4. Формулировка других признаков делимости чисел Основываясь на известных нам признаках делимости и теоремах 1- 4, можно
- 5. Признаки делимости чисел можно классифицировать следующим образом: Делимость по последним цифрам числа Делимость по сумме цифр
- 6. Сложность задач Во множестве отобранных задач на делимость было очень трудно разобраться, но затем удалось разбить
- 7. Первый метод. Разложение на множители (или слагаемые) Задача 1 Доказать, что n3+3n2+5n+3 делится на 3 при
- 8. Второй метод. Исключение целой части числа Задача 2 Найти все целые x и y, удовлетворяющих уравнению
- 9. Третий метод. Равноостаточные классы Задача 4 Доказать, что разность между квадратом числа, которое не делится на
- 10. Четвертый метод. Применение теоремы Безу Задача 5. Доказать, что выражение 35n-2*5n+11n делится на 6 при любом
- 11. Пятый метод. Четность и нечетность чисел Задача 6. Доказать, что уравнение x2+1974=y2 не имеет решений в
- 12. Признаки делимости используются при решении уравнений в целых числах (диофантовы уравнения). Пример 7. Шестой метод. Найти
- 13. Седьмой метод. Бином Ньютона Задача8. Доказать, что 62n+3n+2+3n делится на 11 при всех натуральных n. Решение:
- 14. Выводы: Зная методы исследований признаков делимости натуральных чисел можно сформулировать признаки делимости любых натуральных чисел. Чем
- 16. Скачать презентацию













 Презентация на тему Восточная Сибирь
Презентация на тему Восточная Сибирь  Упрощение выражений
Упрощение выражений Проект «Аналогия» был запущен нами более десяти лет назад и возник как плод сочетания потенциалов юриста и бухгалтера с целью реше
Проект «Аналогия» был запущен нами более десяти лет назад и возник как плод сочетания потенциалов юриста и бухгалтера с целью реше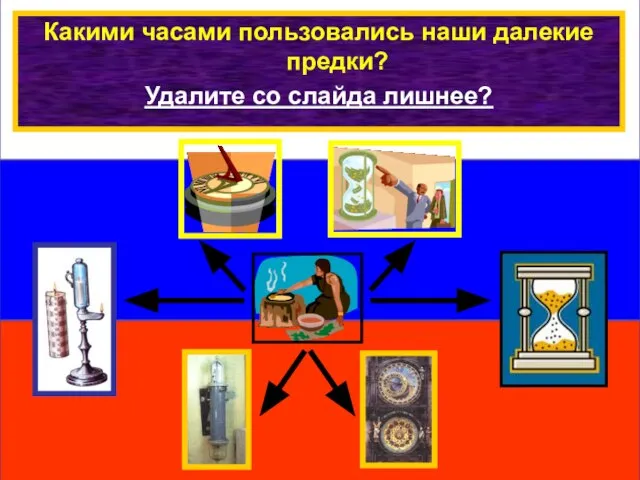 Генеалогия
Генеалогия Колизей в Риме
Колизей в Риме 1С-Битрикс: Корпоративный портал
1С-Битрикс: Корпоративный портал Слова антонимы (Противоположности)
Слова антонимы (Противоположности) Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для коммуникационных провайдеров СТАНДАРТ СЕТЕВОЙ БЕЗО
Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для коммуникационных провайдеров СТАНДАРТ СЕТЕВОЙ БЕЗО Китайский новый год
Китайский новый год 20 причин любить Рёму
20 причин любить Рёму Путь. Перемещение. Определение координаты движущегося тела
Путь. Перемещение. Определение координаты движущегося тела Pancakes day
Pancakes day Критерии и методика отнесения документов к категории для служебного пользования
Критерии и методика отнесения документов к категории для служебного пользования Учебные видеоролики, как ресурс саморазвития
Учебные видеоролики, как ресурс саморазвития Система Box-Design & Nevo
Система Box-Design & Nevo Рекомендуемые подходы определения страховых резервов по договорам страхования жизни На основе Проекта Минфина Правил формирова
Рекомендуемые подходы определения страховых резервов по договорам страхования жизни На основе Проекта Минфина Правил формирова Дома гороскопа
Дома гороскопа Сложение и вычитание десятичных дробей.
Сложение и вычитание десятичных дробей. Судьба старославянизмов в русском языке
Судьба старославянизмов в русском языке Подготовка к написанию изложения по рассказу Л.Н.Толстого «Акула»
Подготовка к написанию изложения по рассказу Л.Н.Толстого «Акула» Обобщающий урок по теме:
Обобщающий урок по теме: Маркетинговые исследования
Маркетинговые исследования  Факторы развития когнитивных способностей в процессе обучения
Факторы развития когнитивных способностей в процессе обучения Доступ к данным на основе ado
Доступ к данным на основе ado Весна. Детские рисунки
Весна. Детские рисунки Декларация на товары
Декларация на товары Химическое действие света. Фотография
Химическое действие света. Фотография Моделирование, как метод познания (10 класс)
Моделирование, как метод познания (10 класс)