Задания на I семестр для инженерно-технических специальностей, специальностей ПСЖД, СЖД, СТР, ЭЖД, СОДП
Содержание
- 2. Аналитическая геометрия на плоскости. Определители второго и третьего порядка. Матрицы. Линейные операции над матрицами. СЛАУ методы
- 3. Рекомендуемая литература: Пайметов Н.Г., Баженова Т.И. Высшая математика (методическое пособие); Данко П.Е. высшая математика в упражнениях
- 4. Прямая линия на плоскости
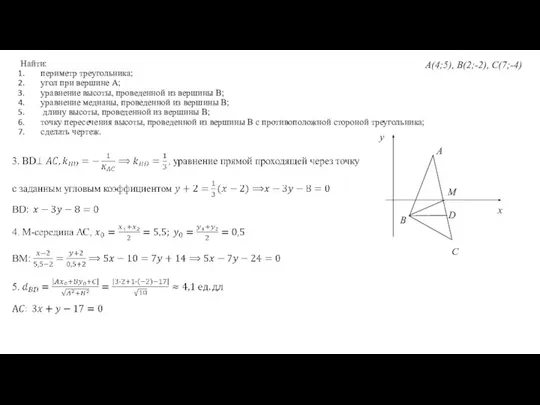
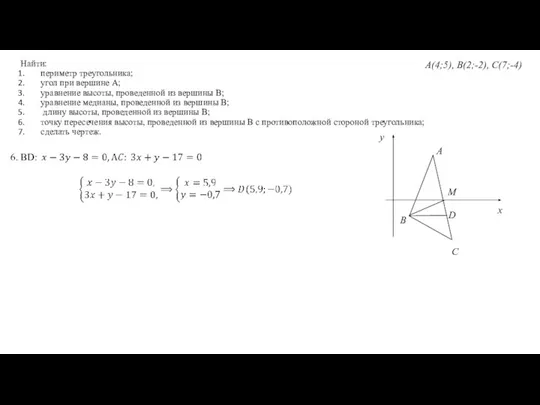
- 11. Пример. Даны координаты вершин треугольника : А(4;5), В(2;-2), С(7;-4) Найти: периметр треугольника; угол при вершине А;
- 12. Найти: периметр треугольника; угол при вершине А; уравнение высоты, проведенной из вершины В; уравнение медианы, проведенной
- 13. Найти: периметр треугольника; угол при вершине А; уравнение высоты, проведенной из вершины В; уравнение медианы, проведенной
- 14. Найти: периметр треугольника; угол при вершине А; уравнение высоты, проведенной из вершины В; уравнение медианы, проведенной
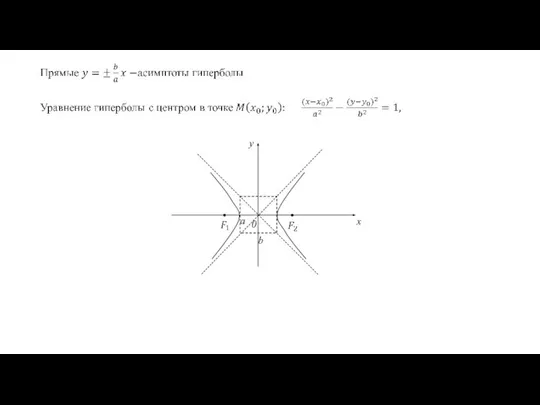
- 15. Кривые второго порядка
- 18. х у a b 0
- 20. х у 0 a b
- 22. х у 0 F M K директриса
- 24. х у 0 1 3 2
- 25. Линейная алгебра. Определители 2-го и 3-го порядков.
- 28. Способы вычисления определителей 3-го порядка:
- 29. Линейная алгебра. Матрицы. Линейный операции над матрицами.
- 34. Системы линейных алгебраических уравнений (СЛАУ)
- 36. Методы решения систем линейных уравнений
- 37. По формулам Крамера
- 39. Средствами матричного исчисления
- 40. Решить систему линейных уравнений матричным методом
- 42. Метод Гаусса Последовательно исключаем неизвестные путем элементарных преобразований, приводя систему к ступенчатому виду. Если в системе
- 44. Элементы векторной алгебры. Аналитическая геометрия в пространстве.
- 49. Плоскость
- 52. Прямая в пространстве
- 58. Разложение вектора по базисным векторам
- 59. -линейная комбинация векторов
- 64. Задания на I семестр для инженерно-технических специальностей, специальностей ЭКО Контрольная работа № 2 (51-100). Библиотека ►
- 65. Комплексные числа. Предел и непрерывность функции. Производная функции одной переменной. Содержание курса:
- 66. Рекомендуемая литература: Пайметов Н.Г., Баженова Т.И. Высшая математика (методическое пособие);
- 67. Комплексные числа
- 68. -тригонометрическая форма записи комплексного числа
- 73. Пределы и непрерывность функции
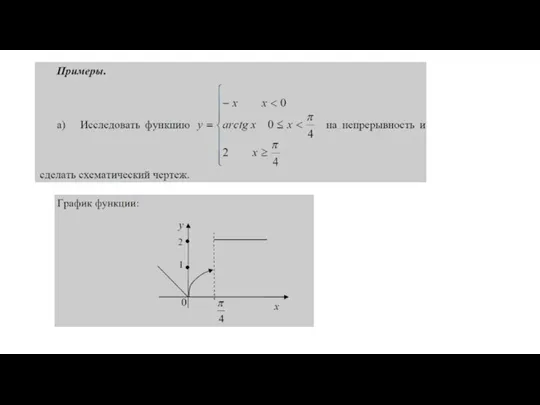
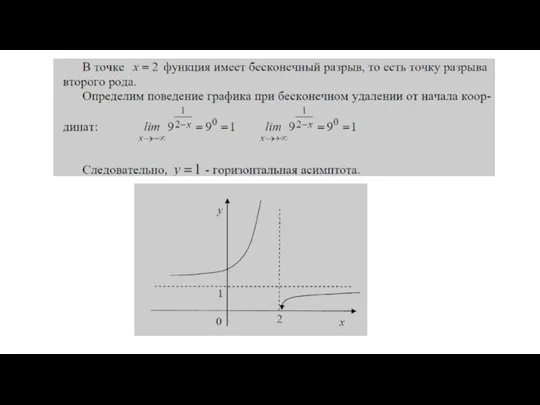
- 80. Непрерывность функции
- 87. Производная функции одной переменной
- 97. Касательная и нормаль к плоской кривой
- 99. Скачать презентацию




































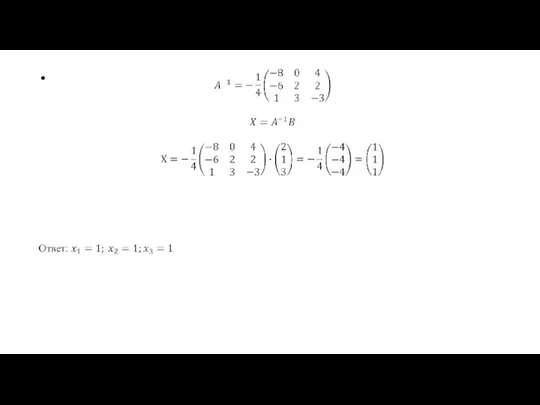






















































 Useless Inventions
Useless Inventions  Моделирование объектов и систем
Моделирование объектов и систем Личное благовестие
Личное благовестие Презентация на тему: Работа классного руководителя с родителями
Презентация на тему: Работа классного руководителя с родителями 2_5325994725348481395
2_5325994725348481395 Организация туриндустрии. Комплекс услуг предприятий питания и его роль в туризме
Организация туриндустрии. Комплекс услуг предприятий питания и его роль в туризме Организация внеурочной деятельности при реализации федерального государственного образовательного стандарта начального общего
Организация внеурочной деятельности при реализации федерального государственного образовательного стандарта начального общего Презентация на тему Формы взаимодействия педагогов с семьей ребенка дошкольного возраста с особыми образовательными потребностя
Презентация на тему Формы взаимодействия педагогов с семьей ребенка дошкольного возраста с особыми образовательными потребностя К вопросу о цикличности развития диатомовых водорослей Байкала
К вопросу о цикличности развития диатомовых водорослей Байкала О мерах, направленных на снижение темпов роста потребительских цен
О мерах, направленных на снижение темпов роста потребительских цен «Своя игра»
«Своя игра» ГУО Туринский учебно-педагогический комплекс детский сад – базовая школа
ГУО Туринский учебно-педагогический комплекс детский сад – базовая школа Презентация на тему Удельный период русской истории (6 класс)
Презентация на тему Удельный период русской истории (6 класс) Красная книга Курганской области
Красная книга Курганской области Презентация на тему have to - must
Презентация на тему have to - must Что такое ДМС страхование? Полис(пластиковый, эл. вариант, бумажный)
Что такое ДМС страхование? Полис(пластиковый, эл. вариант, бумажный) Производство бумаги
Производство бумаги СДД как инструмент хеджирования ценовых рисков в РСВ
СДД как инструмент хеджирования ценовых рисков в РСВ Конкурс курсовых проектов (КМИП)
Конкурс курсовых проектов (КМИП) Менеджмент. Организация, мотивации, контроль, понятие регулирования и его место в системе управления (Часть 3)
Менеджмент. Организация, мотивации, контроль, понятие регулирования и его место в системе управления (Часть 3) Лаборатория 812 – это содружество людей, абсолютно разных, но уже состоявшихся в своих профессиональных сферах. Художники, психолог
Лаборатория 812 – это содружество людей, абсолютно разных, но уже состоявшихся в своих профессиональных сферах. Художники, психолог Должность и прием персонала
Должность и прием персонала Возникновение головных уборов
Возникновение головных уборов Почва – важнейшая часть экосистемы 3 класс
Почва – важнейшая часть экосистемы 3 класс Свойства и функции белков
Свойства и функции белков  Самопрезентация учителя начальных классов
Самопрезентация учителя начальных классов Демонстрационный эксперимент по геометрической оптике
Демонстрационный эксперимент по геометрической оптике Презентация на тему Предложения с вводными конструкциями (8 класс)
Презентация на тему Предложения с вводными конструкциями (8 класс)