ЗАГАДКА МЁБИУСА

План работы
Цели и задачи работы
Объект и предмет исследования
Моделирование объекта исследования
Историческая справка
История создания ленты Мёбиуса
Наука топология
Изучение свойств ленты Мебиуса
Основные свойства ленты Мебиуса
Экспериментальные выводы
Использование ленты Мебиуса
Заключение

Цель работы:
Исследовать поверхность ленты Мебиуса
и ее свойства.
Задачи работы:
Познакомиться с историей появления
ленты Мебиуса.
Выявить и исследовать свойства ленты
Мебиуса.
Установить области применения ленты
Мебиуса.

Объект исследования - Лента Мебиуса
Предмет исследования- свойства ЛМ

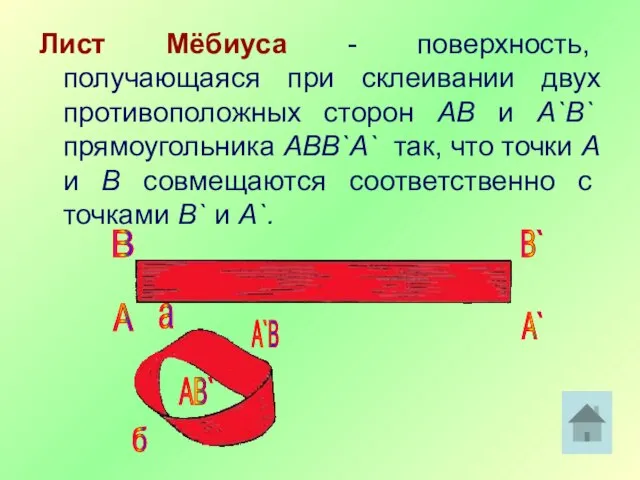
Лист Мёбиуса - поверхность, получающаяся при склеивании двух противоположных сторон AB и А`В` прямоугольника ABB`A` так, что точки А и В совмещаются соответственно с точками B` и A`.

МЕБИУС Август Фердинанд
17.11.1790 - 26.09.1868
Немецкий
- геометр
- астроном - профессор
университета
г. Лейпциг

А жизнь прошла так…
Родился в Шульпфорте (Германия) 17.11.1790
Учился в Лейпццигском университете (1809 – 1813).
Ученик "короля математиков" К. Гаусса
в Геттигенском университете (1813-1814).
В 1814 г. изучал математику в университете в
г. Галле.
С 1816 г. начал вести самостоятельные
астрономические наблюдения в
Плейсенбургской обсерватории.
В 1818 г. стал ее директором, позже –
профессором Лейпцигского университета.
Умер 26.09.1868

Как стал геометром?
Мёбиус был первоначально астрономом, как Гаусс.
В те времена занятия математикой не встречали поддержки, а астрономия давала достаточно денег.
Мёбиус стал одним из крупнейших геометров XIX в.

Самое известное открытие
В 1858г. в возрасте 68 лет Мёбиусу удалось сделать открытие поразительной красоты.
Мебиус послал в Парижскую академию наук работу,
включавшую сведения об этом листе.
7 лет он дожидался рассмотрения своей работы и,
не дождавшись, опубликовал ее результаты.

Есть версия…
Открыть свой «лист» Мёбиусу помогла служанка, сшившая однажды неправильно концы ленты.
2. Придумал ленту Мёбиус, когда наблюдал за горничной, неправильно одевшей на шею свой платок.
Вернее три:
3. Виноват во всём портной, который неправильно вшил манжет рубашки.

Топология
Лист Мёбиуса - топологический
объект, простейшая односторонняя
поверхность с краем.
Сама топология началась именно
с листа Мёбиуса.
Слово это придумал Иоганн Бенедикт
Листинг, который почти в это же время,
что и Мебиус, предложил в качестве
первого примера односторонней
поверхности уже знакомую нам
перекрученную ленту.

Топология
Топология –
«резиновая геометрия»
Топологу ничего не стоит поместить все свои фигуры на поверхность детского надувного шарика и без конца менять его форму, следя лишь за тем, чтобы шарик не лопнул.
А то, что при этом прямые линии, например стороны треугольника, превратятся в кривые, для тополога -безразлично.

Любую фигуру тополог имеет право сгибать,
скручивать, сжимать и растягивать – делать с
ней всё что угодно, только не разрывать и не
склеивать.
При этом он будет считать, что ничего не
произошло, все её свойства остались
неизменными.
Для него не имеют никакого значения
ни расстояния, ни углы, ни площади.
Топология

Близким «странным» геометрическим объектом является бутылка Клейна. Бутылка Клейна может быть получена путем склеивания двух лент Мёбиуса по краям.

Основные свойства
ленты Мебиуса
односторонность,
непрерывность,
связность,
ориентированность
“хроматический номер”

ЛМ имеет 1 край
ЛМ имеет одну поверхность
ЛМ имеет одну искривленную поверхность, и
если по ней двигаться, можно с внутренней
части переместиться на внешнюю.
ЛМ получается из прямоугольника, у которого
длина намного больше ширины.
Если закрашивать одну сторону ЛМ, не
пересекая края, то в итоге закрасится вся
поверхность ленты
Если пустить по поверхности ЛМ движущиеся
объекты, они будут двигаться бесконечно долго.
Экспериментальные выводы

Главная ценность листа Мёбиуса
Дал мощный толчок новым обширным математическим исследованиям.
Мёбиуса часто считают символом современной математики.

Наука и техника
Свойство односторонности листа Мебиуса было использовано в технике:
если в ременной передачи ремень сделать в виде листа Мебиуса, то его поверхность будет изнашиваться вдвое медленнее, чем у обычного кольца;
- это дает ощутимую экономию.

Магнитофонная пленка, соединенная
таким образом, записывает звук на
обеих сторонах.
Магнитофон прокручивает пленку в
виде ленты Мебиуса вдвое дольше,
чем обычную.
Это удваивает время записи
Наука и техника

В матричных принтерах красящая лента
также имела вид лист Мёбиуса;
это для увеличения срока годности.
Наука и техника

Есть фильтры, в которых жидкость
пропускают сквозь ленту из
фильтрующего материала.
В 1971 году изобретатель с Урала
Чесноков П.Н. применил фильтр в виде
листа Мёбиуса
Наука и техника

Фотографии образцов конструкций, использующих лист Мёбиуса
Силовая конструкция (квадратная), мешалка (большая круглая), винты, испытывающиеся на модели судна (два маленьких круглых)
Наука и техника

Трансформатор
Наука и техника

Лента Мебиуса понравилась не
только математикам,
но и фокусникам.
Более 100 лет лента Мёбиуса
используется для показа
различных фокусов и
развлечений.
Применение

Международный символ переработки
Мотив Ленты Мебиуса встречается в названиях художественных произведений, общественных заведений, логотипах.

Лента Мебиуса вдохновила многих
художников и на создание известных
скульптур, картин и для графического
искусства .
Лист Мебиуса в искусстве

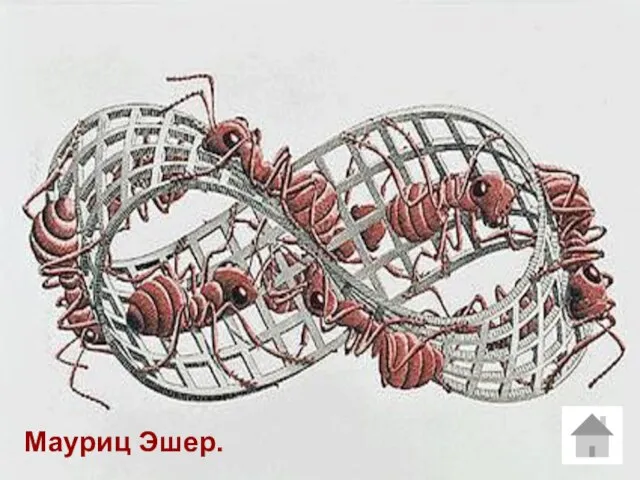
Лист Мебиуса в искусстве
Довольно много разнообразных
рисунков оставил голландский художник Мауриц Эшер.
Особенно интересна гравюра с
изображением муравья,
ползающего по Ленте Мебиуса.

Мауриц Эшер.