Содержание
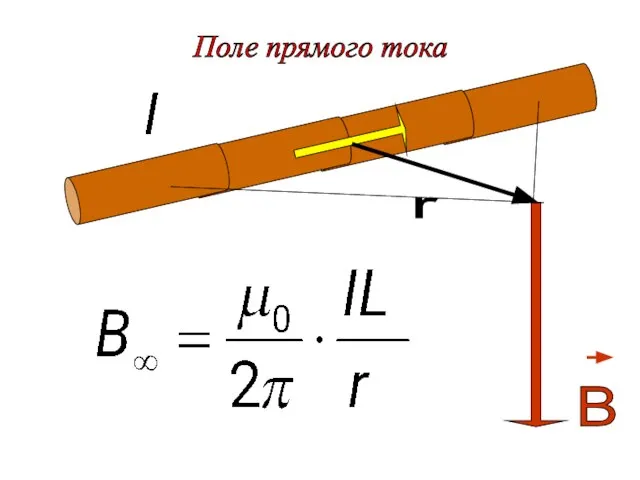
- 2. Магнитное поле прямого тока. Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от
- 3. Для конечного проводника угол α изменяется от α1 до α2. Тогда: Для бесконечно длинного проводника α1
- 4. Поле прямого тока
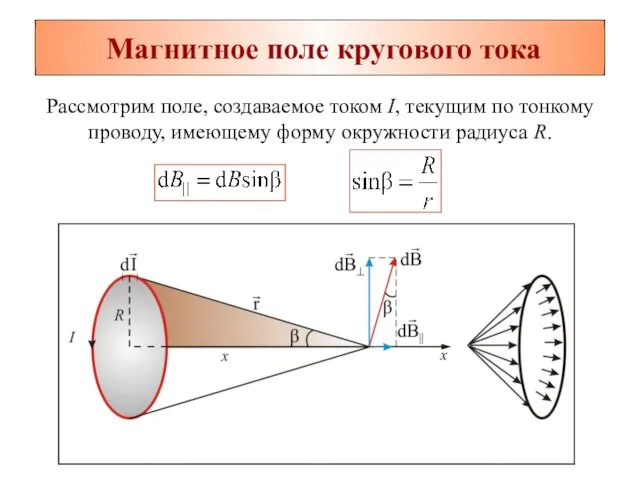
- 5. Магнитное поле кругового тока Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности
- 6. т.к. угол между и α – прямой, то тогда получим: (1.6.1)
- 7. Подставив в (1.6.1) и, проинтегрировав по всему контуру получим выражение для нахождения магнитной индукции кругового тока:
- 8. Поле кругового тока
- 9. Заметим, что в числителе – магнитный момент контура. Тогда, на большом расстоянии от контура, при ,
- 10. Рассмотрим еще одно важное следствие из закона Био–Савара–Лапласа, которое облегчает расчеты магнитных полей. Допустим, что по
- 11. Поэтому направление обхода и напрваление тока должны быть связаны правилом знаков: Если буравчик вращать по выбранному
- 12. Интеграл называется циркуляцией вектора напряженности вдоль данной замкнутой линии обхода. Теорема о циркуляции напряженности магнитного поля
- 13. Теорема Гаусса для вектора магнитной индукции (1.7.1) Поток вектора через замкнутую поверхность должен быть равен нулю.
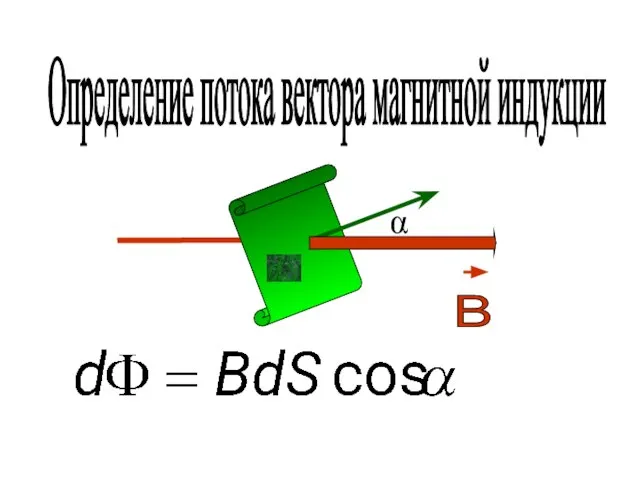
- 14. α Определение потока вектора магнитной индукции dS
- 15. В природе нет магнитных зарядов – источников магнитного поля, на которых начинались и заканчивались бы линии
- 16. Магнитное поле обладает тем свойством, что его дивергенция всюду равна нулю: или Электростатического поля может быть
- 17. Основные уравнения магнитостатики Основные уравнения магнитостатики для магнитных полей, созданных постоянными потоками зарядов, записанные в дифференциальной
- 18. Магнитные линии образуют петли вокруг токов. Не имея ни конца, ни начала, линии В возвращаются в
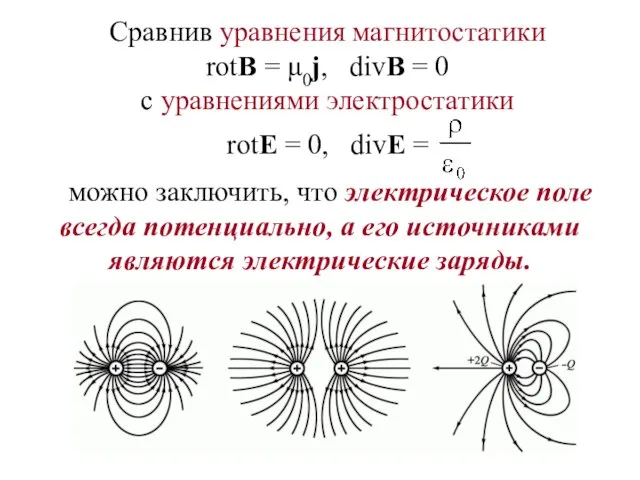
- 19. Сравнив уравнения магнитостатики rotВ = μ0j, divВ = 0 с уравнениями электростатики rotЕ = 0, divЕ
- 20. Поле движущегося заряда Полагая, что в элементе тока I·dl содержится Δn электронов, имеющих скорости упорядоченного движения
- 21. Напряженность магнитного поля внутри длинного соленоида с током Соленоид в магнетизме – аналог конденсатора в электричестве.
- 22. Второй и четвертый интегралы равны нулю, т.к. , а третьим интегралом пренебрегаем, ввиду малости поля вне
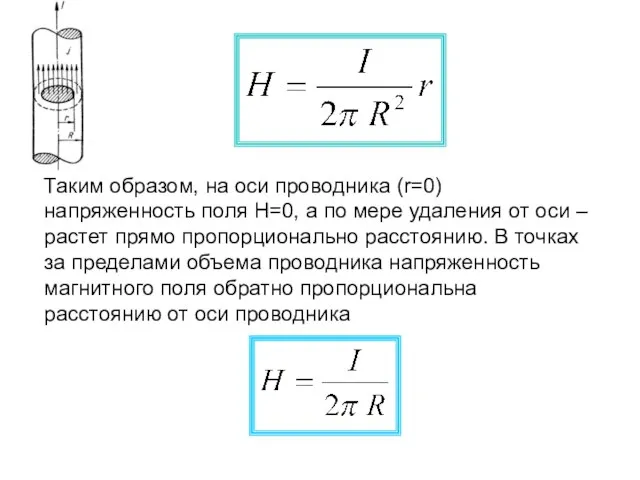
- 23. напряженность магнитного поля внутри толстых проводников с током Если проводник прямолинейный и бесконечно длинный, то вдоль
- 24. Таким образом, на оси проводника (r=0) напряженность поля Н=0, а по мере удаления от оси –
- 25. Закон Ампера F = I·L·B·sina I - сила тока в проводнике; B - модуль вектора индукции
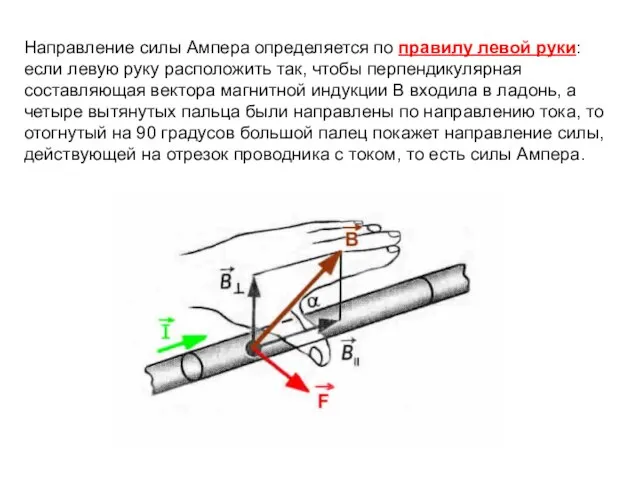
- 26. Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая
- 27. Зная закон Ампера, можно получить выражение для силы, с которой магнитное поле действует на движущийся заряд.
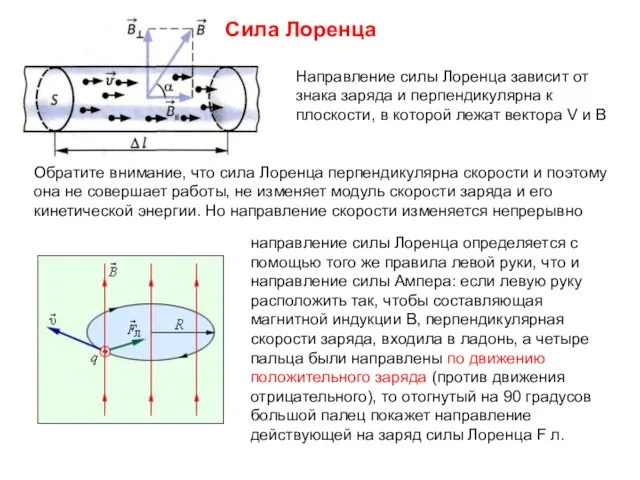
- 28. Сила Лоренца Направление силы Лоренца зависит от знака заряда и перпендикулярна к плоскости, в которой лежат
- 29. Если имеются одновременно электрическое и магнитное поля, то на заряд действует сила Пусть два одноименных точечных
- 30. Отношение магнитной силы к электрической будет: то есть магнитная сила слабее кулоновской силы на множитель, пропорциональный
- 31. Значение величины μ0 содержится в определении силы Ампера : 1Ампер=1А это сила неизменяющегося тока, который, проходя
- 34. Скачать презентацию


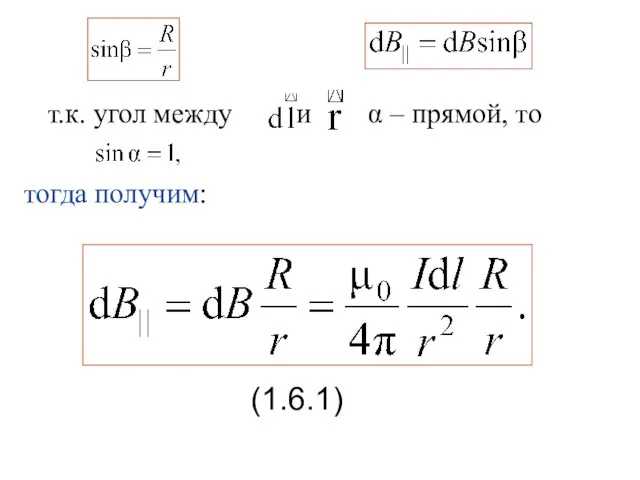

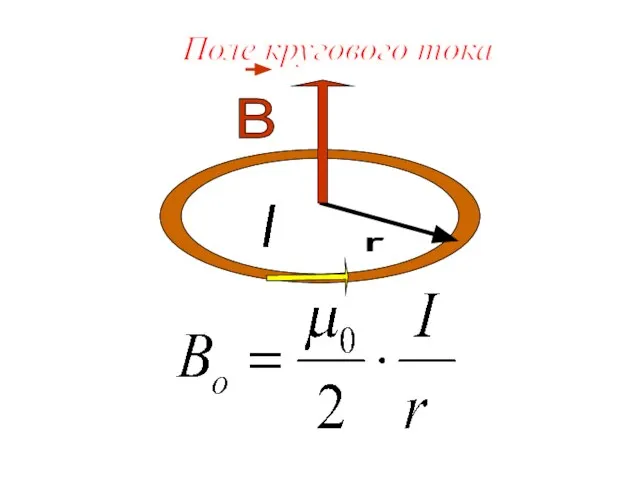



















 Денежные переводы физических лиц: состояние и тенденции развития (на примере ПАО Сбербанк)
Денежные переводы физических лиц: состояние и тенденции развития (на примере ПАО Сбербанк) Особенности истории информатики
Особенности истории информатики Мотивирование топ-менеджеров в банковской сфере: подходы и инструменты
Мотивирование топ-менеджеров в банковской сфере: подходы и инструменты = 1
= 1 Изустная среда мордовского села
Изустная среда мордовского села Показатели рыночной активности
Показатели рыночной активности Выхухоль. Красная книга
Выхухоль. Красная книга Обработка текстовой и графической информации. Создаём комбинированный документ
Обработка текстовой и графической информации. Создаём комбинированный документ Телевидение: я выбираю или меня выбирают. Автор и руководитель проекта: Симонова Ольга Владимировна 2004 год
Телевидение: я выбираю или меня выбирают. Автор и руководитель проекта: Симонова Ольга Владимировна 2004 год Что я сделаю, чтобы доверенный мне магазин стал лучшим на рынке
Что я сделаю, чтобы доверенный мне магазин стал лучшим на рынке Туалетная вода для мужчин Faberlic Intense
Туалетная вода для мужчин Faberlic Intense Межпроцедурные анализы и оптимизации
Межпроцедурные анализы и оптимизации Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны
Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны Урок 3 Человек и Бог в православии-повторение
Урок 3 Человек и Бог в православии-повторение 17 век
17 век ПЕРЕГОВОРЫ
ПЕРЕГОВОРЫ Изготовление вечернего платья
Изготовление вечернего платья Теорiя iгор
Теорiя iгор  Презентация на тему Роль гормонов в обмене веществ, росте и развитии организма биология 8 класс
Презентация на тему Роль гормонов в обмене веществ, росте и развитии организма биология 8 класс аня хочет санчо панчо
аня хочет санчо панчо Создание таблиц в Microsoft Word
Создание таблиц в Microsoft Word Teenagers’ society problems
Teenagers’ society problems Воля познавать
Воля познавать Любимое блюдо моей семьи
Любимое блюдо моей семьи Ладья. Урок №8
Ладья. Урок №8 Описательные характеристики распределения тестовых результатов
Описательные характеристики распределения тестовых результатов Презентация на тему Одиночество
Презентация на тему Одиночество Ich gehe mit meine Laterne
Ich gehe mit meine Laterne