Закон Ома

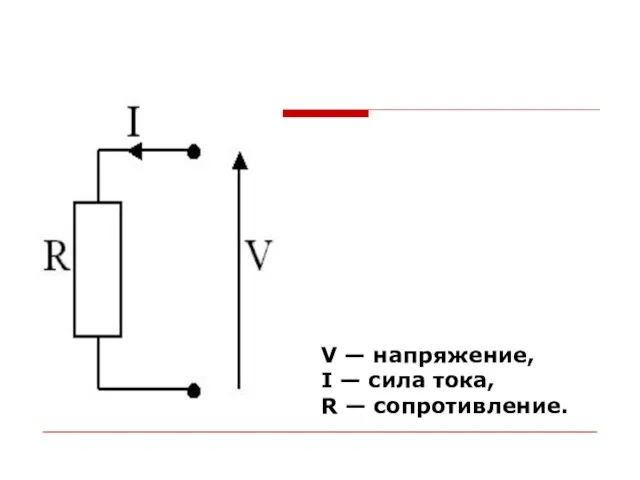
V — напряжение,
I — сила тока,
R — сопротивление.

Закон Ома записывается формулой:
Где: I — сила тока (А), U — напряжение (В), R — сопротивление(Ом).

Следует иметь в виду, что закон Ома является фундаментальным (основным) и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков .

История закона Ома
Ом, проводя эксперименты с проводником, установил, что сила тока в проводнике пропорциональна напряжению , приложенному к его концам:
I∼U,
или
Коэффициент пропорциональности G назвали электропроводностью, а величину R=1/G принято именовать электрическим сопротивлением проводника.
Закон Ома был открыт в 1826 году.

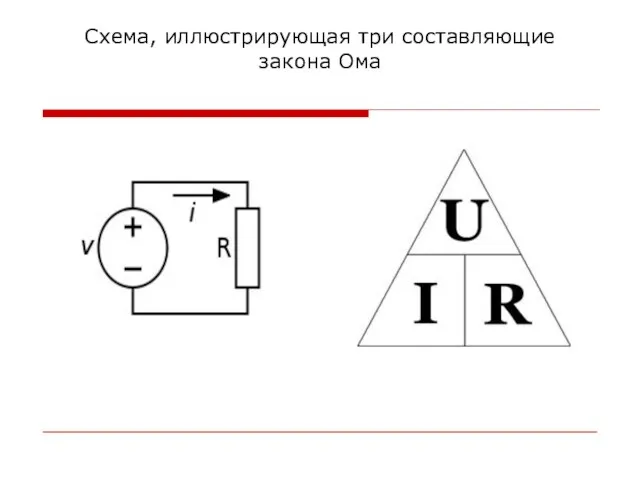
Схема, иллюстрирующая три составляющие закона Ома

Закон Ома в дифференциальной форме
Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.
Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
Где:
j — вектор плотности тока,
Q — удельная проводимость,
E — вектор напряжённости электрического поля.

Закон Ома для переменного тока
Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
tде:
U = U0eiωt — напряжение или разность потенциалов,
I — сила тока,
Z = Re—iδ — комплексное сопротивление (импеданс),
R = (Ra²+Rr²)1/2 — полное сопротивление,
Rr = ωL — 1/ωC — реактивное сопротивление
Rа — активное сопротивление, не зависящее от частоты,
δ = —arctg Rr/Ra — сдвиг фаз между напряжением и силой тока.
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится