ЗАКОНОМЕРНОСТИ ПЕРЕНОСА НОСИТЕЛЕЙ ЗАРЯДА В НИЗКОРАЗМЕРНЫХ СТРУКТУРАХ

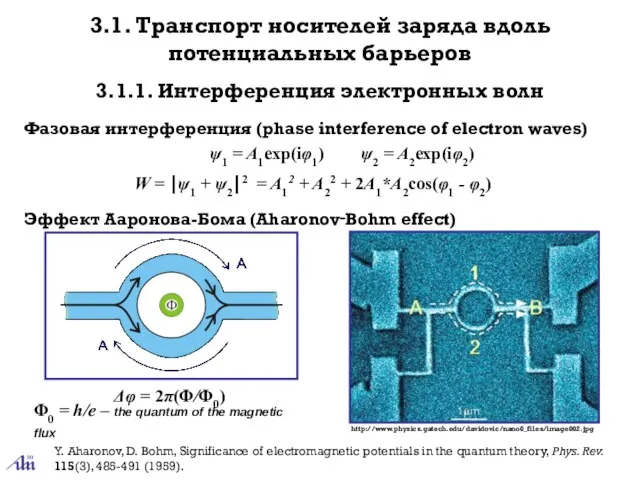
3.1.1. Интерференция электронных волн
3.1. Транспорт носителей заряда вдоль потенциальных барьеров
W = ⎪ψ1 + ψ2⎪2 = A12 + A22 + 2A1*A2cos(φ1 - φ2)
Фазовая интерференция (phase interference of electron waves)
Эффект Ааронова-Бома (Aharonov‑Bohm effect)
Φ0 = h/e – the quantum of the magnetic flux
Y. Aharonov, D. Bohm, Significance of electromagnetic potentials in the quantum theory, Phys. Rev. 115(3), 485-491 (1959).
Δφ = 2π(Φ/Φ0)
http://www.physics.gatech.edu/davidovic/nano0_files/image002.jpg

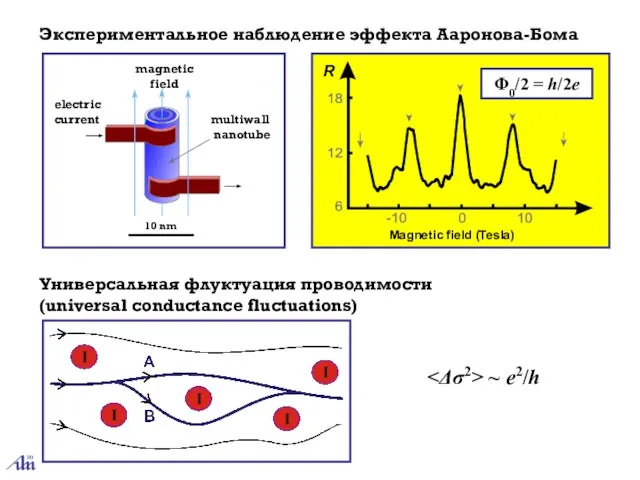
Экспериментальное наблюдение эффекта Ааронова-Бома
Φ0/2 = h/2e
Универсальная флуктуация проводимости
(universal conductance fluctuations)
<Δσ2> ~ e2/h

3.1.2. Вольт-амперные характеристики
низкоразмерных структур
Формализм Ландауэра-Бютикера (Landauer‑Büttiker formalism)
Ii = 2evi(dni/dE)Δμi
Ii = (2e/h)Δμi
R. Landauer, Spatial variation of currents and fields due to localized scatters in metallic conduction, IBM J. Res. Dev. 1(6), 223-231 (1957); M. Büttiker, Four-terminal phase-coherent conductance, Phys. Rev. Lett. 57(14), 1761-1764 (1986).
μi = eVi

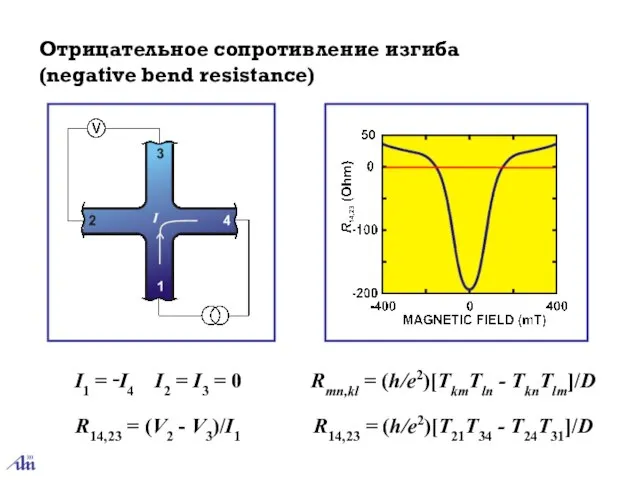
Отрицательное сопротивление изгиба
(negative bend resistance)
R14,23 = (V2 - V3)/I1
Rmn,kl = (h/e2)[TkmTln - TknTlm]/D
R14,23 = (h/e2)[T21T34 - T24T31]/D

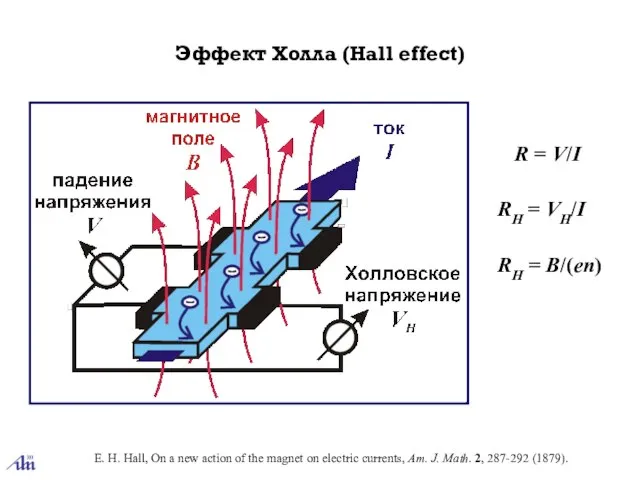
Эффект Холла (Hall effect)
R = V/I
RH = VH/I
RH = B/(en)
E. H. Hall, On a new action of the magnet on electric currents, Am. J. Math. 2, 287-292 (1879).

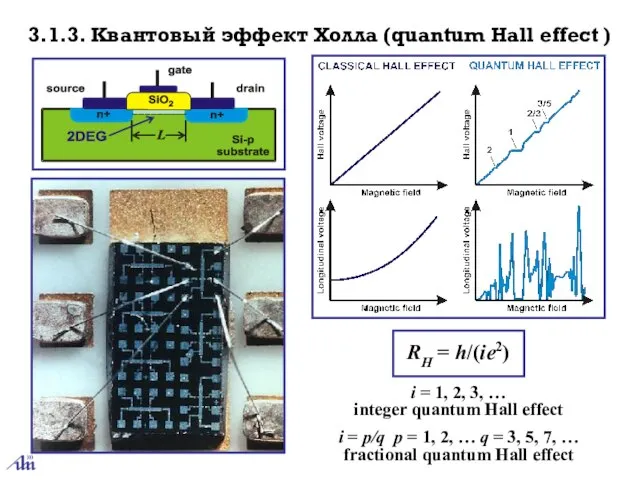
3.1.3. Квантовый эффект Холла (quantum Hall effect )
i = 1, 2, 3, …
integer quantum Hall effect
RH = h/(ie2)
i = p/q p = 1, 2, … q = 3, 5, 7, …
fractional quantum Hall effect

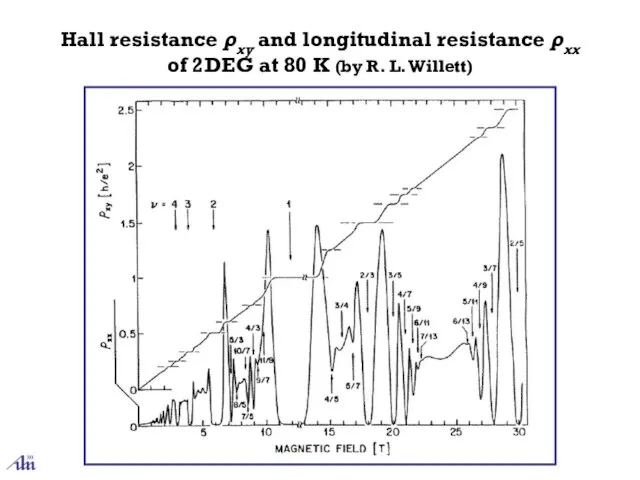
Hall resistance ρxy and longitudinal resistance ρxx
of 2DEG at 80 K (by R. L. Willett)

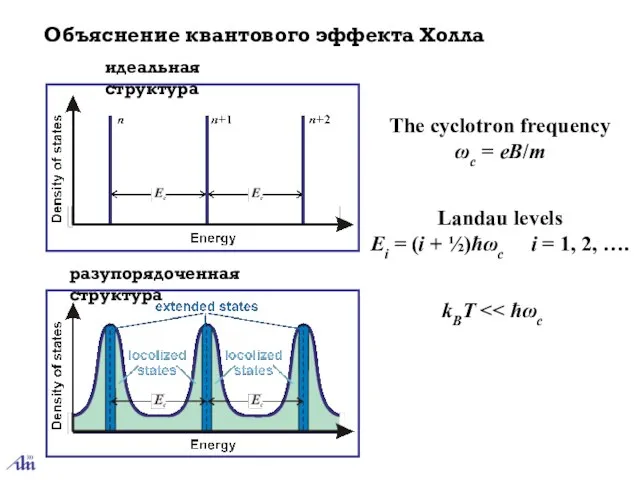
Объяснение квантового эффекта Холла
The cyclotron frequency
ωc = eB/m
Landau levels
Ei = (i + ½)ħωc i = 1, 2, ….
kBT << ħωc
идеальная структура
разупорядоченная структура

for the discovery of the quantized Hall effect
Klaus von Klitzing
(1943)
Max-Planck-Institut für Festkörperforschung
Stuttgart, Germany
The Nobel Prize in Physics, 1985
K. von Klitzing, G. Dorda, M. Pepper, New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance, Phys. Rev. Lett. 45(6), 494-497 (1980) – the integer quantum Hall effect
From the History of the Quantum Hall Effect

for their discovery of a new form of quantum fluid with fractionally charged excitations
The Nobel Prize in Physics, 1998
From the History of the Quantum Hall Effect
D. C. Tsui, H. L. Störmer, A. C. Gossard, Two-dimensional magnetotransport in the extreme quantum limit, Phys. Rev. Lett. 48(22), 1559-1562 (1982) and R. B. Laughlin, Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations, Phys. Rev. Lett. 50(18), 1395-1398 (1983) – the fractional quantum Hall effect
Robert B. Laughlin
(1950)
Stanford University
Stanford, CA, USA
Horst L. Störmer
(1943)
Columbia University
New York, NY, USA
Daniel C. Tsui
(1939)
Princeton University
Princeton, NJ, USA

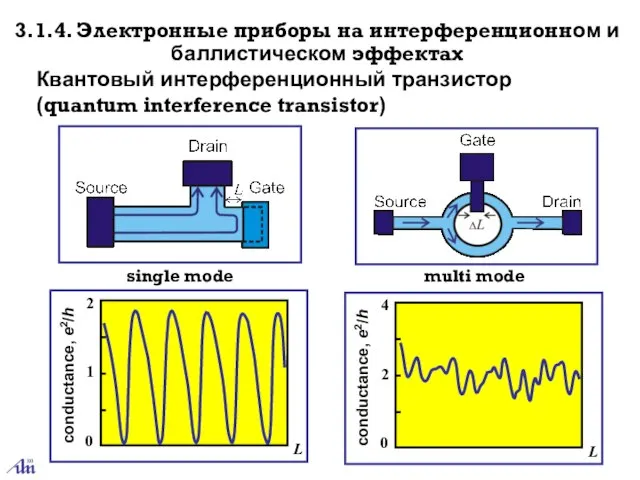
3.1.4. Электронные приборы на интерференционном и баллистическом эффектах
Квантовый интерференционный транзистор
(quantum interference transistor)
single mode
multi mode

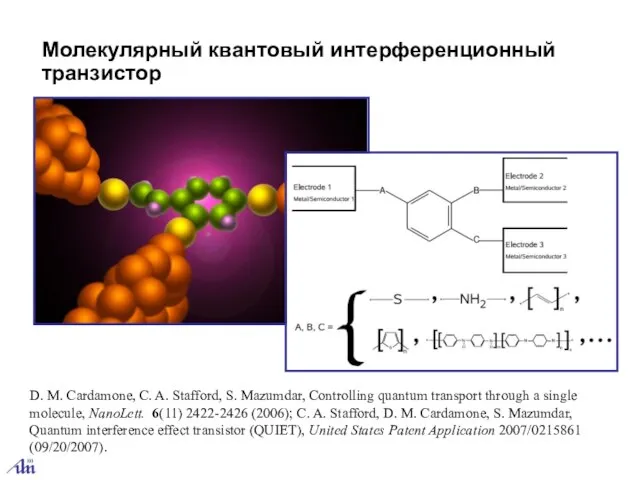
Молекулярный квантовый интерференционный транзистор
D. M. Cardamone, C. A. Stafford, S. Mazumdar, Controlling quantum transport through a single molecule, NanoLett. 6(11) 2422-2426 (2006); C. A. Stafford, D. M. Cardamone, S. Mazumdar, Quantum interference effect transistor (QUIET), United States Patent Application 2007/0215861 (09/20/2007).

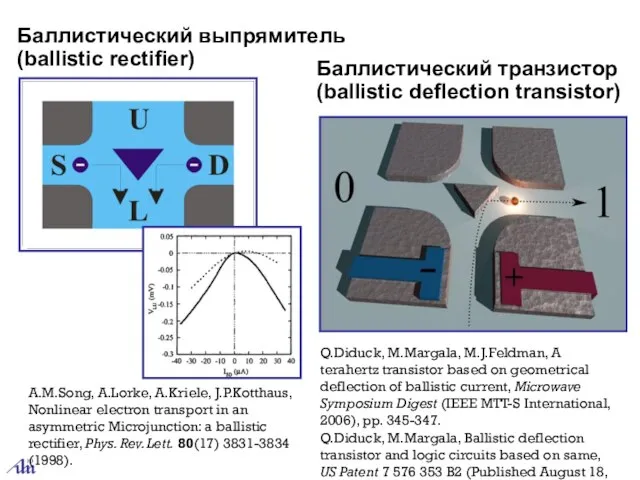
Баллистический транзистор
(ballistic deflection transistor)
Q.Diduck, M.Margala, M.J.Feldman, A terahertz transistor based on geometrical deflection of ballistic current, Microwave Symposium Digest (IEEE MTT-S International, 2006), pp. 345-347.
Q.Diduck, M.Margala, Ballistic deflection transistor and logic circuits based on same, US Patent 7 576 353 B2 (Published August 18, 2009).
Баллистический выпрямитель
(ballistic rectifier)
A.M.Song, A.Lorke, A.Kriele, J.P.Kotthaus, Nonlinear electron transport in an asymmetric Microjunction: a ballistic rectifier, Phys. Rev. Lett. 80(17) 3831-3834 (1998).

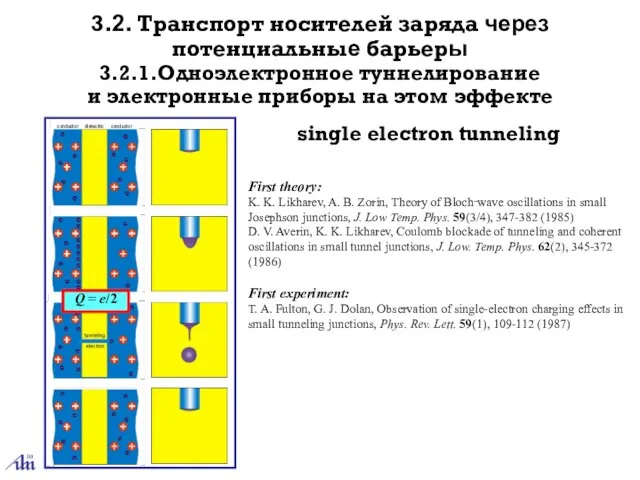
Q = e/2
3.2.1.Одноэлектронное туннелирование
и электронные приборы на этом эффекте
3.2. Транспорт носителей заряда через потенциальные барьеры
single electron tunneling
First theory:
K. K. Likharev, A. B. Zorin, Theory of Bloch‑wave oscillations in small Josephson junctions, J. Low Temp. Phys. 59(3/4), 347-382 (1985)
D. V. Averin, K. K. Likharev, Coulomb blockade of tunneling and coherent oscillations in small tunnel junctions, J. Low. Temp. Phys. 62(2), 345-372 (1986)
First experiment:
T. A. Fulton, G. J. Dolan, Observation of single-electron charging effects in small tunneling junctions, Phys. Rev. Lett. 59(1), 109-112 (1987)

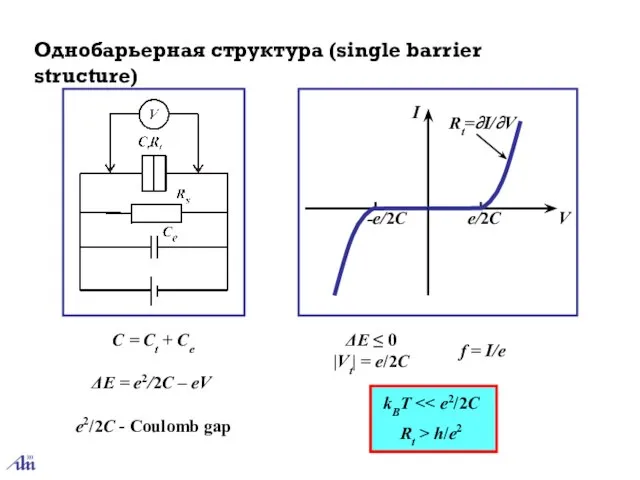
ΔE = e2/2C – eV
C = Ct + Ce
ΔE ≤ 0
|Vt| = e/2C
e2/2C - Coulomb gap
Однобарьерная структура (single barrier structure)
f = I/e
kBT << e2/2C
Rt > h/e2
V
I
Rt=∂I/∂V
e/2C
-e/2C

Двухбарьерная структура (double barrier structure)
ΔE = 1/2[(e/C + ΔVo)2C –ΔVo2C]
V ≥ C(e/2C + ΔVo)/CR
Coulomb staircase
V
I
e/2C
-e/2C
ΔV0
I
1
3
5
VC/e
N=0
-1
-2
C ≈ CR >> CL
C = CL + CR

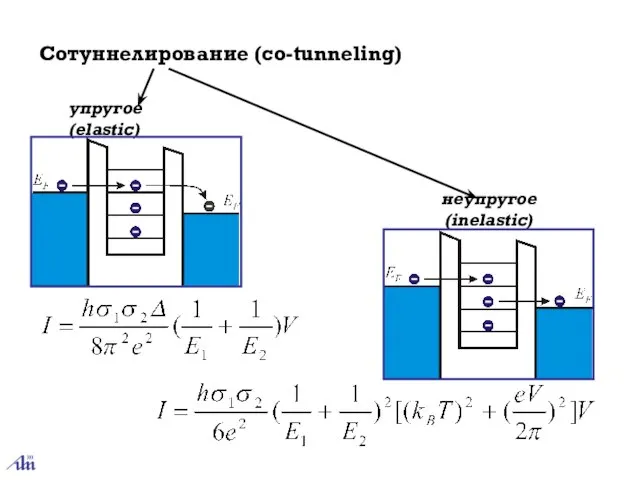
Сотуннелирование (co-tunneling)
упругое (elastic)
неупругое (inelastic)

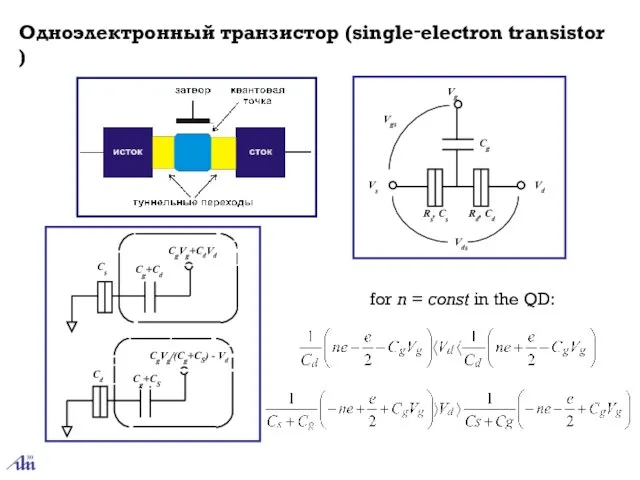
for n = const in the QD:
Одноэлектронный транзистор (single‑electron transistor )

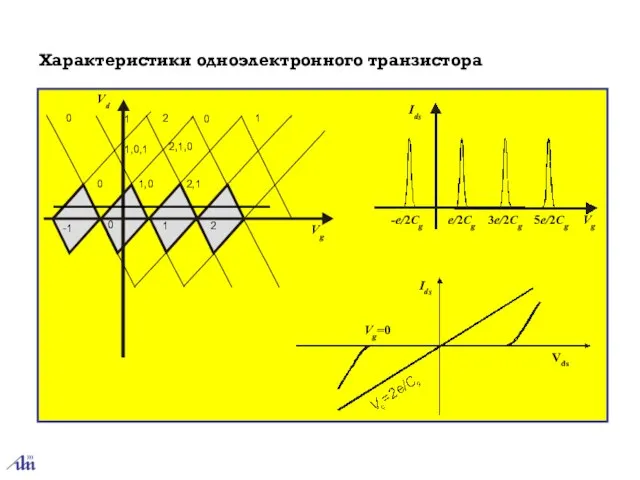
Характеристики одноэлектронного транзистора

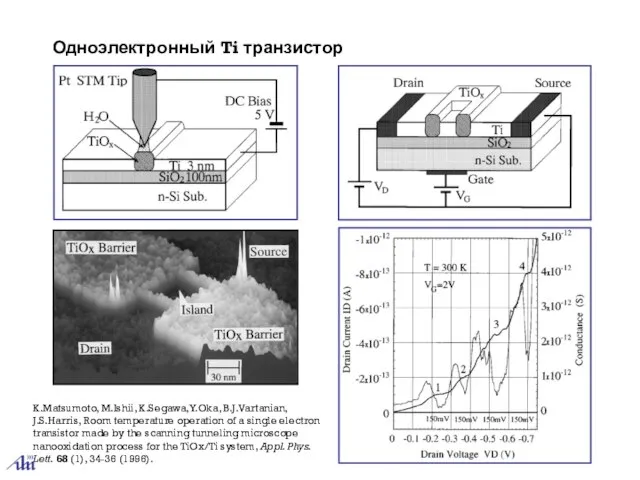
Одноэлектронный Ti транзистор
K.Matsumoto, M.Ishii, K.Segawa,Y.Oka, B.J.Vartanian, J.S.Harris, Room temperature operation of a single electron transistor made by the scanning tunneling microscope nanooxidation process for the TiOx/Ti system, Appl. Phys. Lett. 68 (1), 34-36 (1996).

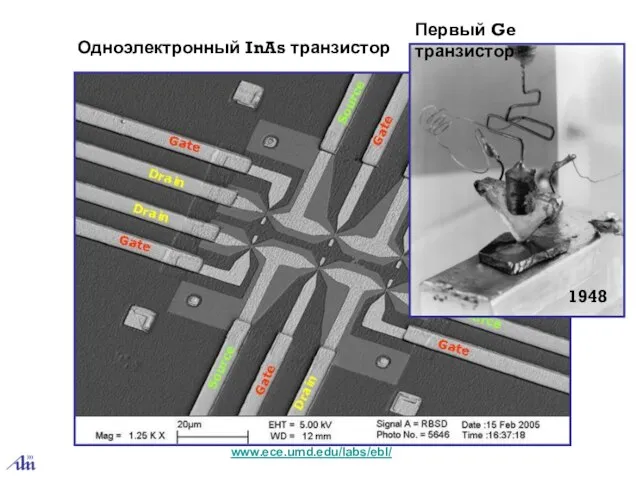
www.ece.umd.edu/labs/ebl/
Одноэлектронный InAs транзистор
1948
Первый Ge транзистор

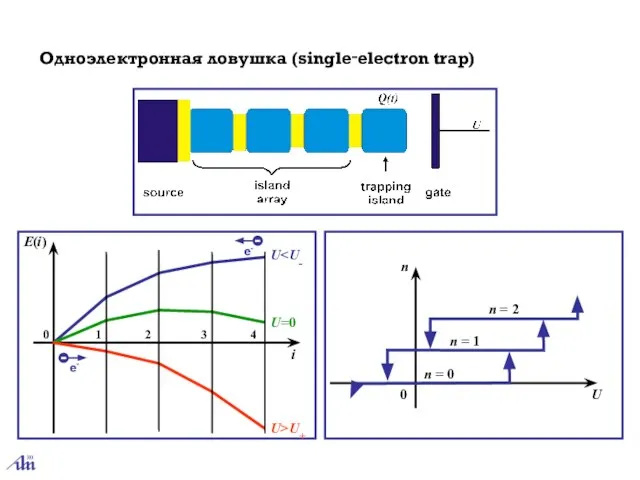
Одноэлектронная ловушка (single‑electron trap)
0
1
2
3
4
U=0
U>U+
U
i
E(i)
n
0
U
n = 2
n = 1
n = 0

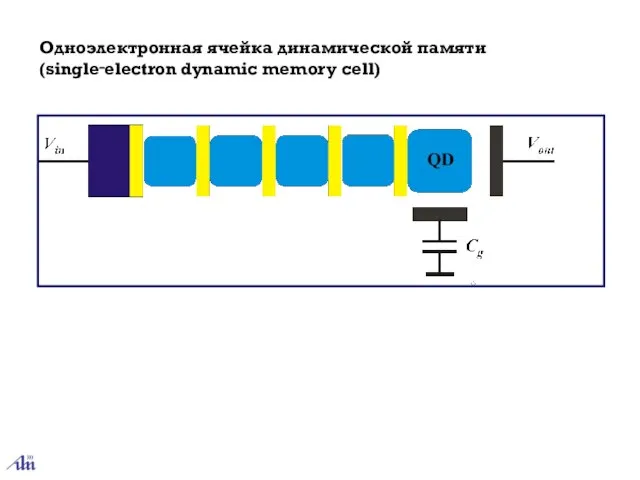
Одноэлектронная ячейка динамической памяти (single‑electron dynamic memory cell)

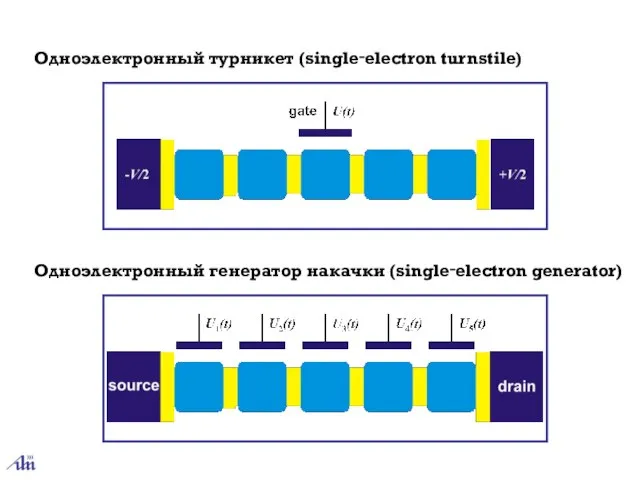
Одноэлектронный турникет (single‑electron turnstile)
Одноэлектронный генератор накачки (single‑electron generator)

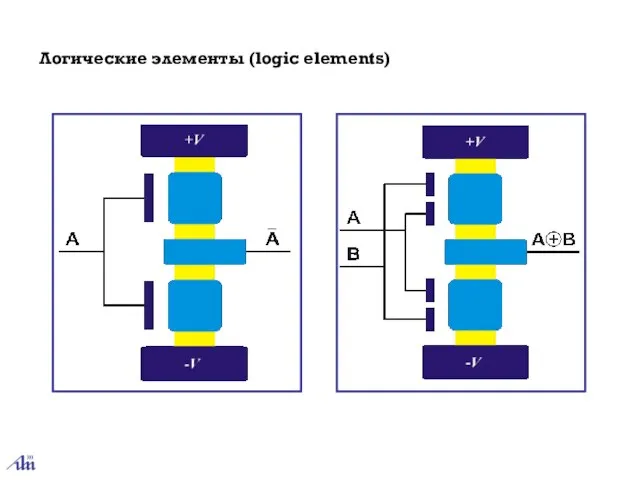
Логические элементы (logic elements)

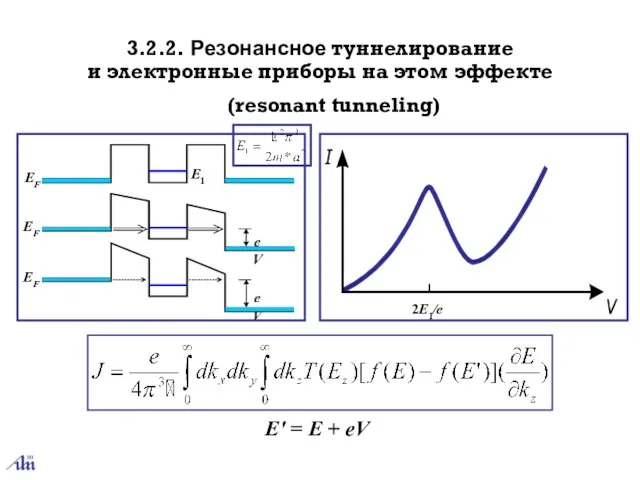
E' = E + eV
3.2.2. Резонансное туннелирование
и электронные приборы на этом эффекте
(resonant tunneling)

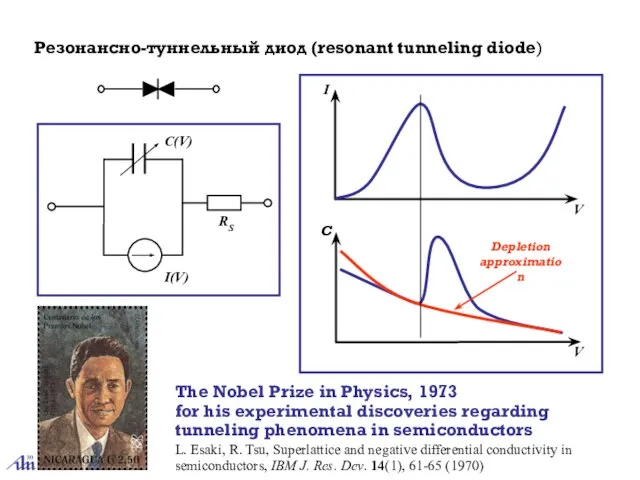
Резонансно-туннельный диод (resonant tunneling diode)
V
I
C
Depletion
approximation
V
L. Esaki, R. Tsu, Superlattice and negative differential conductivity in semiconductors, IBM J. Res. Dev. 14(1), 61-65 (1970)
The Nobel Prize in Physics, 1973
for his experimental discoveries regarding tunneling phenomena in semiconductors

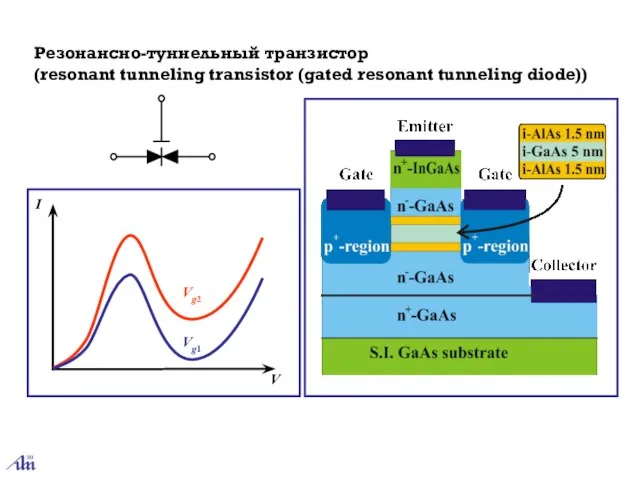
Резонансно-туннельный транзистор
(resonant tunneling transistor (gated resonant tunneling diode))
V
I
Vg1
Vg2

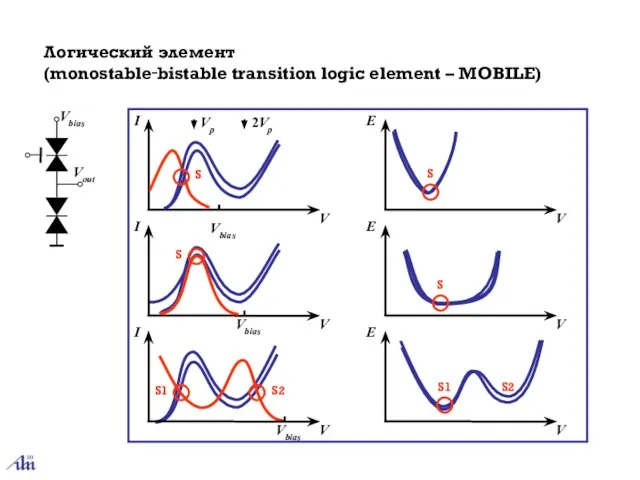
Логический элемент
(monostable‑bistable transition logic element – MOBILE)
S
Vp
2Vp
Vbias
V
I
V
E
S
Vbias
V
I
S
V
E
S
Vbias
V
I
S1
S2
V
E
S1
S2

3.3. Спинтроника (spintronics)
область науки и техники, занимающаяся созданием, исследованием и применением электронных приборов, в которых спин электрона наравне с его зарядом используется для обработки информации

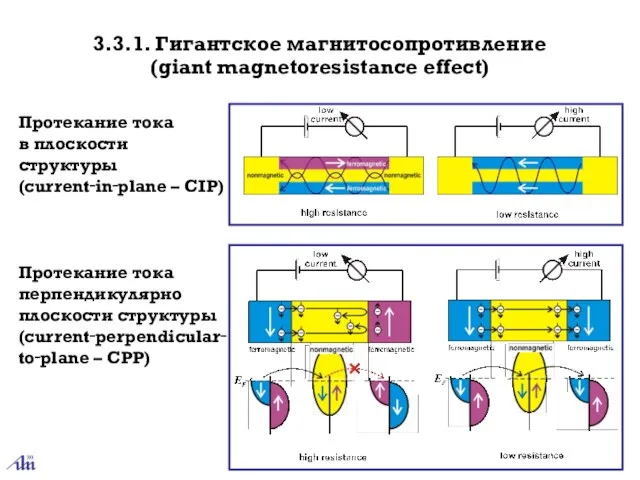
3.3.1. Гигантское магнитосопротивление
(giant magnetoresistance effect)
Протекание тока
в плоскости структуры
(current‑in‑plane – CIP)
Протекание тока
перпендикулярно
плоскости структуры
(current‑perpendicular‑
to‑plane – CPP)

The Nobel Prize in Physics, 2007
From the History of the Giant Magnetoresistance Effect
Albert Fert
(1938)
Université Paris-Sud
Orsay, France
Peter Grünberg
(1939)
Forschungszentrum Jülich
Jülich, Germany
for the discovery of Giant Magnetoresistance
M. N. Baibich, J. M. Broto, A. Fert, F. N. Van Dau, F. Petroff, Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices, Phys. Rev. Lett. 61(21), 2472-2475 (1988).
G. Binasch, P. Grünberg, F. Saurenbach, W. Zinn, Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange, Phys. Rev. B 39(7), 4828-4830 (1989).

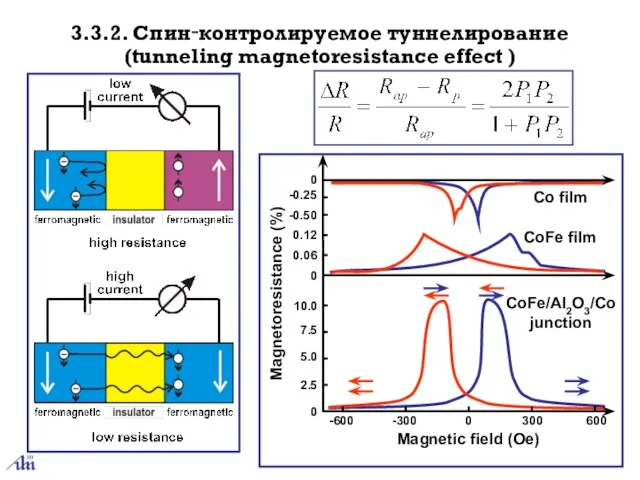
3.3.2. Спин‑контролируемое туннелирование
(tunneling magnetoresistance effect )
Co film
CoFe film
CoFe/Al2O3/Co
junction
Magnetic field (Oe)
Magnetoresistance (%)

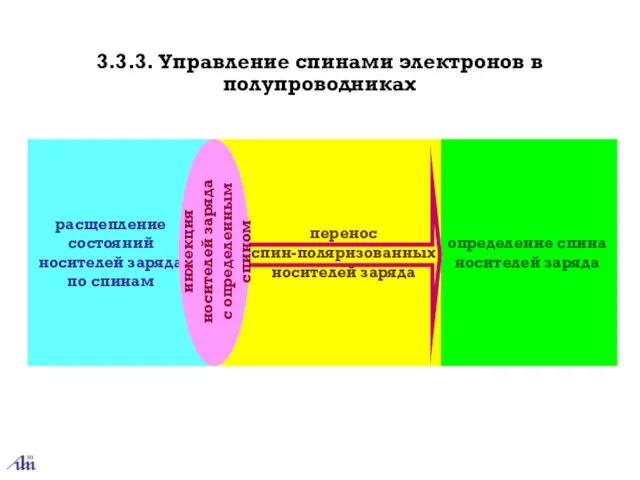
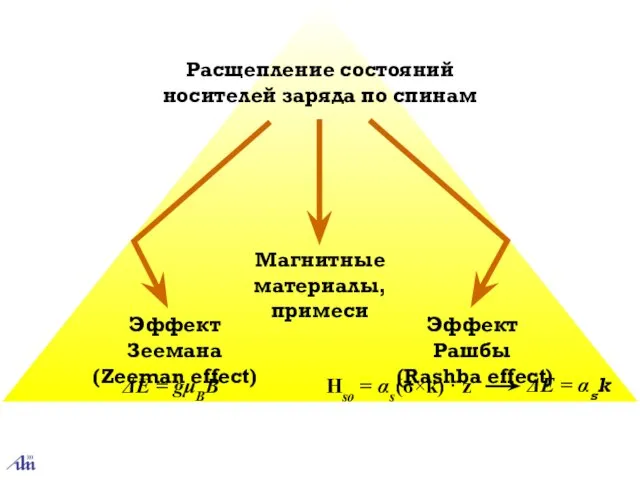
расщепление
состояний
носителей заряда
по спинам
3.3.3. Управление спинами электронов в полупроводниках
перенос
спин-поляризованных
носителей заряда
определение спина
носителей заряда
инжекция
носителей заряда
с определенным спином

Расщепление состояний
носителей заряда по спинам
Эффект Зеемана
(Zeeman effect)
Эффект Рашбы
(Rashba effect)
ΔE = gμBB
Hso = αs(σ×k) · z
ΔE = αsk
Магнитные материалы,
примеси

Перенос спин-поляризованных носителей заряда
(механизмы спин-релаксации в полупроводниках)
Механизм Бира-Аронова-Пикуса
(Bir-Aronov-Pikus mechanism)
Механизм Эллиота-Яфета
(Elliot-Yafet mechanism)
Механизм Дьяконова-Перела
(D’yakonov-Perel mechanism)
Следствие обменного взаимодействия и рекомбинации электронов и дырок. Низкие Т,
р-полупроводники.
Следствие спин-орбитального рассеивания, при столкновении электронов с фононами или примесями. Низкие и умеренные Т.
Следствие спин-расщепления зоны проводимости. Повышенные Т.
сверхтонкое взаимодействие спинов электронов и спинов ядер (hyperfine interaction of the electron spins and nuclear spins)

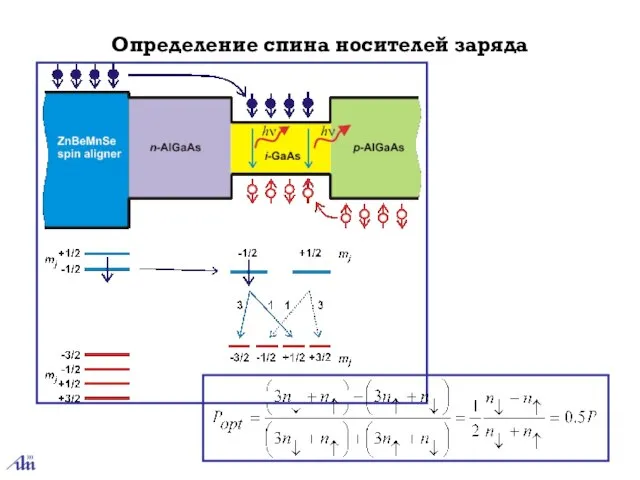
Определение спина носителей заряда

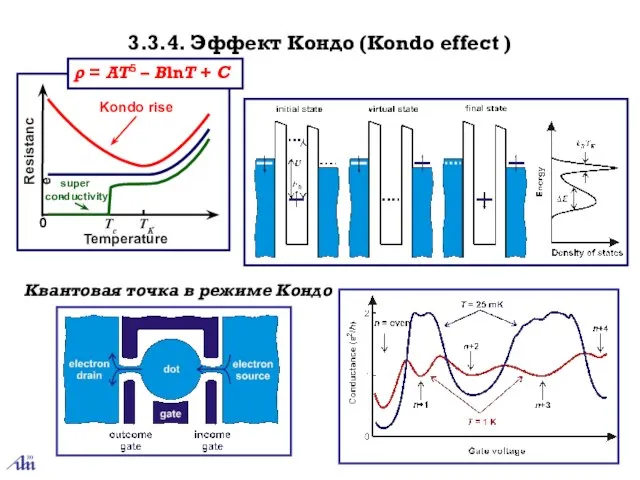
Temperature
Resistance
super-
conductivity
Tc
TK
Квантовая точка в режиме Кондо
ρ = AT5 – BlnT + C
Kondo rise
3.3.4. Эффект Кондо (Kondo effect )
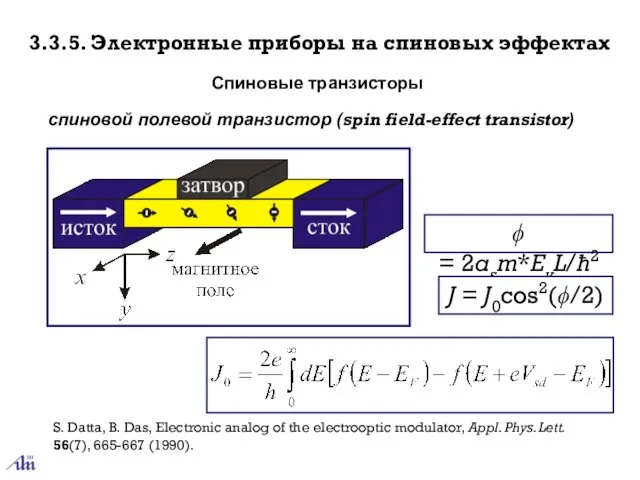
0

3.3.5. Электронные приборы на спиновых эффектах
Спиновые транзисторы
спиновой полевой транзистор (spin field-effect transistor)
S. Datta, B. Das, Electronic analog of the electrooptic modulator, Appl. Phys. Lett. 56(7), 665-667 (1990).
ϕ = 2αsm*EyL/ħ2
J = J0cos2(ϕ/2)

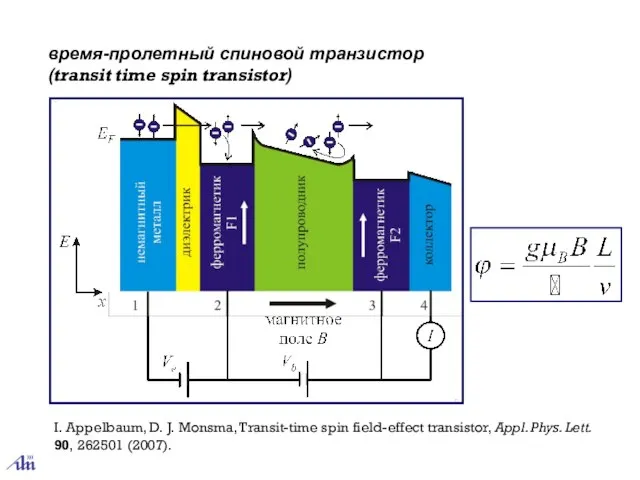
время-пролетный спиновой транзистор
(transit time spin transistor)
I. Appelbaum, D. J. Monsma, Transit-time spin field-effect transistor, Appl. Phys. Lett. 90, 262501 (2007).

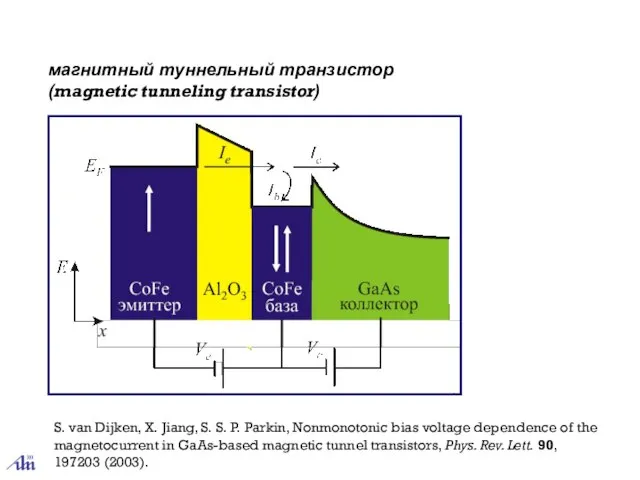
магнитный туннельный транзистор
(magnetic tunneling transistor)
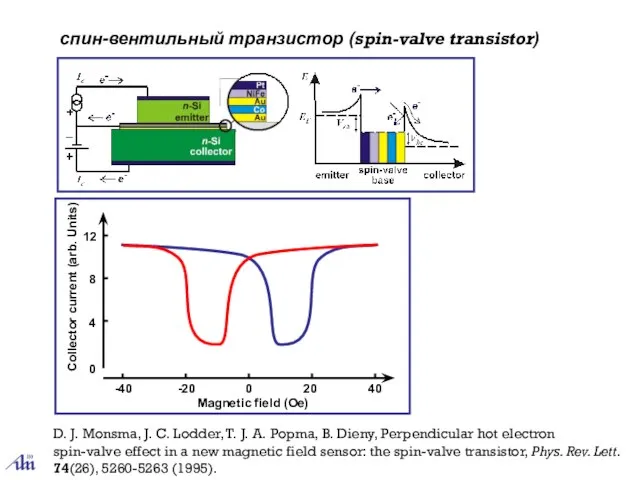
S. van Dijken, X. Jiang, S. S. P. Parkin, Nonmonotonic bias voltage dependence of the magnetocurrent in GaAs-based magnetic tunnel transistors, Phys. Rev. Lett. 90, 197203 (2003).

спин-вентильный транзистор (spin-valve transistor)
Magnetic field (Oe)
Collector current (arb. Units)
D. J. Monsma, J. C. Lodder, T. J. A. Popma, B. Dieny, Perpendicular hot electron spin-valve effect in a new magnetic field sensor: the spin-valve transistor, Phys. Rev. Lett. 74(26), 5260-5263 (1995).

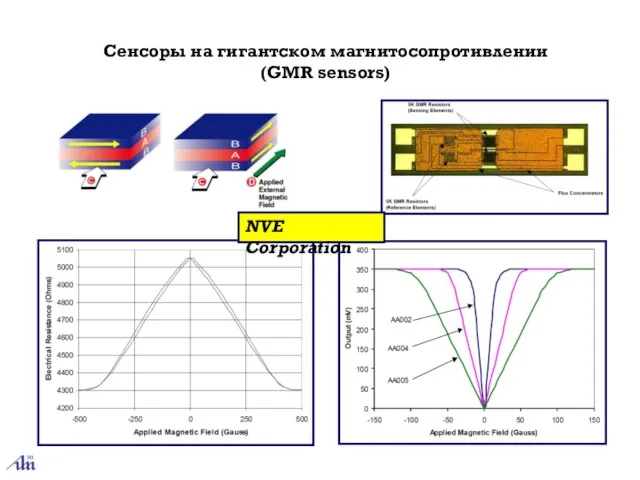
Сенсоры на гигантском магнитосопротивлении
(GMR sensors)
NVE Corporation

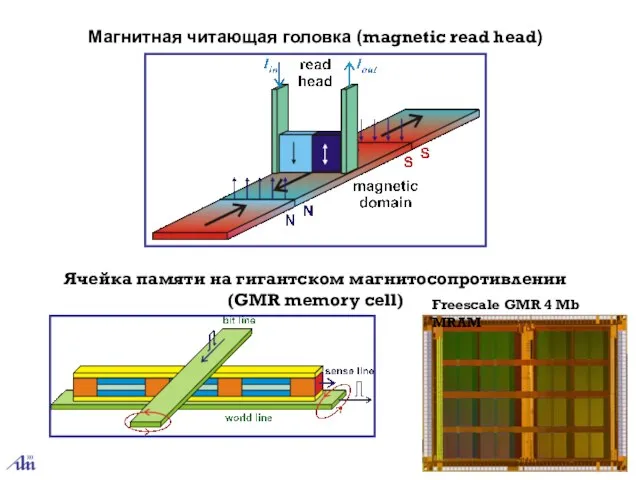
Магнитная читающая головка (magnetic read head)
Ячейка памяти на гигантском магнитосопротивлении
(GMR memory cell)
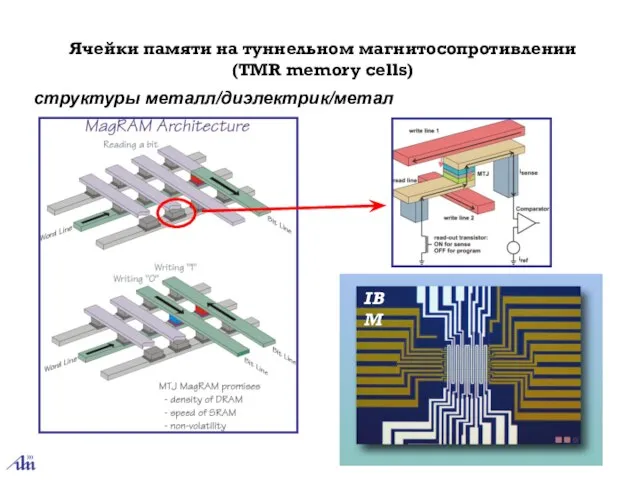
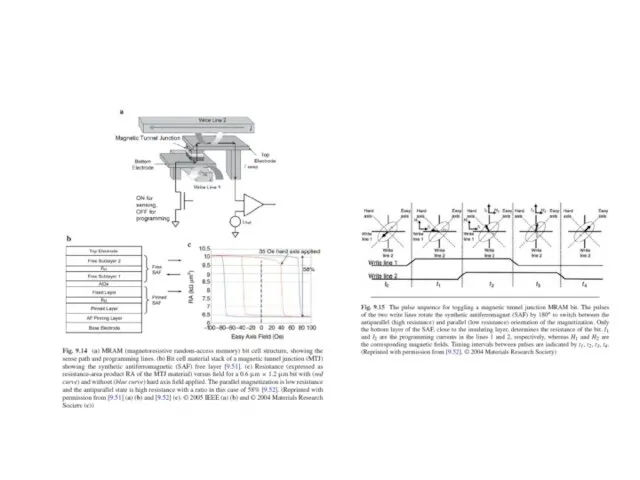
Freescale GMR 4 Mb MRAM

Ячейки памяти на туннельном магнитосопротивлении
(TMR memory cells)
структуры металл/диэлектрик/метал