Содержание
- 2. План Закон противоречия Закон исключенного третьего Закон тождества
- 3. В логике, как и во всякой науке, главное — законы.
- 4. Закон противоречия Закон противоречия говорит о противоречащих друг другу высказываниях, т. е. о таких высказываниях, одно
- 5. Пример Трава зелёная Трава не является зеленой
- 6. Закон непротиворечия Закон противоречия говорит о противоречащих высказываниях — отсюда его название. Но он отрицает противоречие,
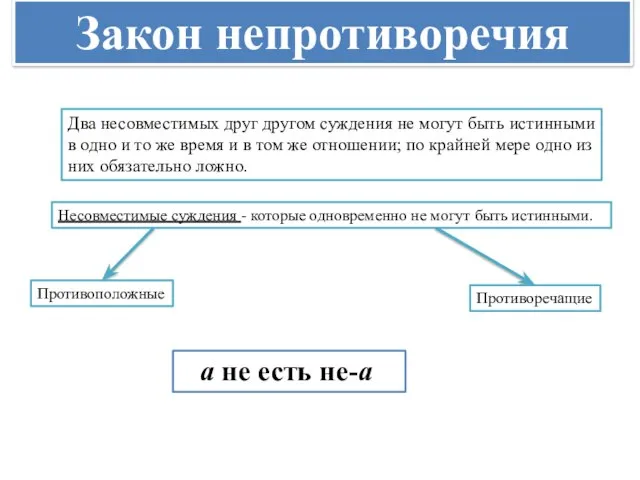
- 7. Закон непротиворечия Два несовместимых друг другом суждения не могут быть истинными в одно и то же
- 8. Условия закона непротиворечия: В процессе мышления необходимо утверждать принадлежность предмету (явлению) одного признака и в то
- 9. Закон исключенного третьего Из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано. Закон
- 10. Пример Аристотель умер в 322 г. до н.э. или он не умер в этом году
- 11. Истинность отрицания равнозначна ложности утверждения. В силу этого закон исключенного третьего можно передать и так: каждое
- 12. «...Невозможно, — писал Аристотель, — чтобы одно и то же в одно и то же время
- 13. Закон тождества В процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе.
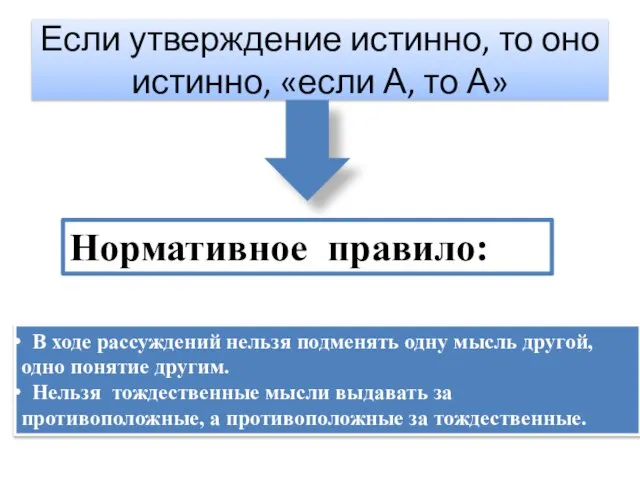
- 14. Если утверждение истинно, то оно истинно, «если А, то А» Нормативное правило: В ходе рассуждений нельзя
- 16. Скачать презентацию











 SEO или продвижение сайта в поисковых системах.
SEO или продвижение сайта в поисковых системах. Ділова атрибутика
Ділова атрибутика МЕЖДУНАРОДНОЕ ГУМАНИТАРНОЕ ПРАВО(МГП) –
МЕЖДУНАРОДНОЕ ГУМАНИТАРНОЕ ПРАВО(МГП) – психология упр 2
психология упр 2 Малые капиталистические страны Западной Европы (общий обзор)
Малые капиталистические страны Западной Европы (общий обзор) Здоровое питание – основа долголетия
Здоровое питание – основа долголетия «Организация исследовательской деятельности учащихся».
«Организация исследовательской деятельности учащихся». Театральный коллектив Премьера. Спектакль Морозко по мотивам русской народной сказки
Театральный коллектив Премьера. Спектакль Морозко по мотивам русской народной сказки Музыкальные инструменты
Музыкальные инструменты КВАДРАТ И КУБ ЧИСЛА
КВАДРАТ И КУБ ЧИСЛА Классификация органических соединений
Классификация органических соединений Инфекция срс аса кауыпты инфекция
Инфекция срс аса кауыпты инфекция Малые архитектурные формы
Малые архитектурные формы New money
New money Презентация на тему Глухие и звонкие парные согласные в корне слова
Презентация на тему Глухие и звонкие парные согласные в корне слова Презентация на тему Архитектура и ее функции
Презентация на тему Архитектура и ее функции Эскизы. Выполнение эскиза. Урок 20
Эскизы. Выполнение эскиза. Урок 20 559 О, возвещайте вы о Христе
559 О, возвещайте вы о Христе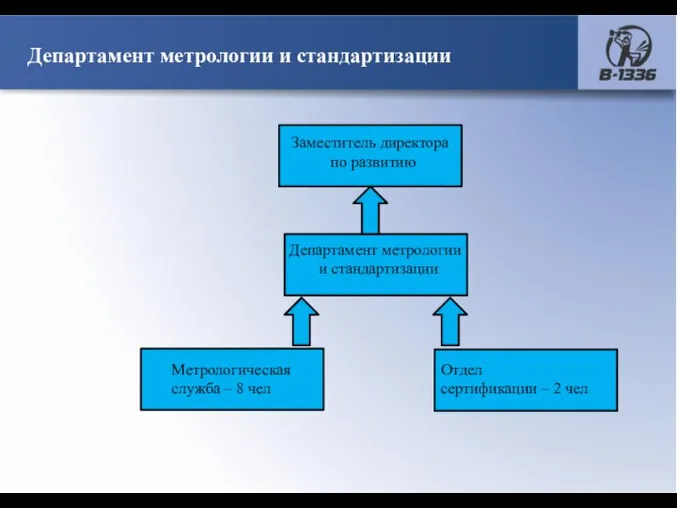 Департамент метрологии и стандартизации
Департамент метрологии и стандартизации Презентация урока русского языка
Презентация урока русского языка о
о Виды предприятий. Предпринимательство и бизнес
Виды предприятий. Предпринимательство и бизнес Презентация на тему Природа России
Презентация на тему Природа России  vb
vb Кондитерское производство
Кондитерское производство Презентация на тему Знакомство учащихся с искусством Японии на занятиях оригами
Презентация на тему Знакомство учащихся с искусством Японии на занятиях оригами Лекция 5. Структура населения
Лекция 5. Структура населения Культура поведения человека
Культура поведения человека