Законы постоянного тока. Электрический ток, основные характеристики

Электрический ток может распределяться по поверхности проводника или области пространства, где происходит упорядоченное движение зарядов неравномерно.
Плотность тока - физическая величина, измеряемая зарядом, протекающим за единицу времени через единицу поверхности проводника.
Плотность тока – вектор перпендикулярный к поверхности через которую протекает ток.
За направление вектора плотности тока выбирают направление движения положительных зарядов.
Если в каждой точке пространства известен вектор плотности тока, то сила тока определяется как поток вектора плотности тока через поверхность.
Единица плотности тока в СИ — ампер на метр в квадрате (А/м2).

Под действием кулоновских сил носители тока в проводнике будут перемещаться до тех пор, пока потенциалы во всех точках цепи не станут равными.
Это приведет к исчезновению электрического поля, а следовательно, и к исчезновению электрического тока.
Постоянный ток при наличии лишь сил электростатического происхождения невозможен. Для поддержания в цепи постоянного тока необходимы устройства, способные создавать и поддерживать в цепи разность потенциалов за счет работы сил неэлектростатического происхождения.
Такие устройства называют источниками тока (напряжения).
Силы неэлектростатического происхождения, действующие на заряженные частицы со стороны источников тока, называют сторонними (т.е. посторонними не электростатического происхождения).
Природа сторонних сил может быть различной.
В гальванических элементах сторонние силы возникают за счет химических реакций между электродами и электролитами,
В генераторах — за счет механической энергии вращения ротора генератора.

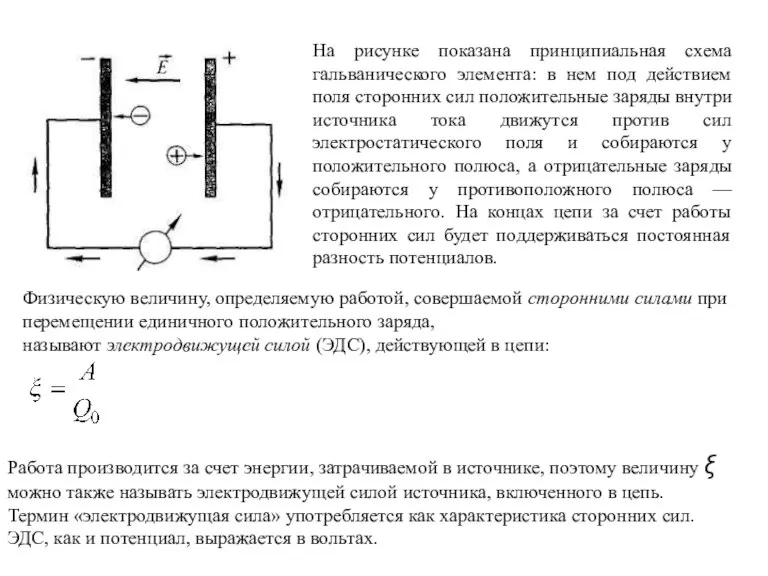
На рисунке показана принципиальная схема гальванического элемента: в нем под действием поля сторонних сил положительные заряды внутри источника тока движутся против сил электростатического поля и собираются у положительного полюса, а отрицательные заряды собираются у противоположного полюса — отрицательного. На концах цепи за счет работы сторонних сил будет поддерживаться постоянная разность потенциалов.
Физическую величину, определяемую работой, совершаемой сторонними силами при перемещении единичного положительного заряда,
называют электродвижущей силой (ЭДС), действующей в цепи:
Работа производится за счет энергии, затрачиваемой в источнике, поэтому величину ξ можно также называть электродвижущей силой источника, включенного в цепь.
Термин «электродвижущая сила» употребляется как характеристика сторонних сил.
ЭДС, как и потенциал, выражается в вольтах.

Физическую величину, определяемую работой, совершаемой
суммарным полем электростатических (кулоновских) сил и сторонних сил,
на данном участке цепи (1-2),
при перемещении единичного положительного заряда, называют напряжением U на участке цепи (1-2).
Понятие напряжения является обобщением понятия разности потенциалов.
В случае замкнутой цепи, концы замкнуты и потенциалы равны, тогда работа электростатических сил равна нулю
Напряжение на концах 1 и 2 участка цепи равно разности потенциалов в том случае, если на этом участке не действует ЭДС, т. е. сторонние силы отсутствуют.

Сопротивление и проводимость проводников
Сопротивление R (электрическое сопротивление) проводника - величина, характеризующая сопротивление проводника (или электрической цепи) электрическому току.
Единица сопротивления в СИ - ом (Ом). 1 Ом - сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А.
Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен.
Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S
ρ - коэффициент пропорциональности, характеризующий материал проводника и называемый
удельным электрическим сопротивлением.
Удельное электрическое сопротивление проводника - физическая величина, определяемая электрическим сопротивлением однородного линейного проводника длиной 1 м и площади поперечного сечения 1 м2.
Величина ρ служит характеристикой вещества, из которого изготовлен проводник.

В таблице приведены значения удельных сопротивлений для различных проводников, откуда следует, что наименьшее ρ имеет серебро,
но на практике ввиду меньшей стоимости и плотности чаще используют медные алюминиевые провода.

Электрическая проводимость (электропроводность) количественно характеризует способность проводника пропускать электрический ток.
Единица проводимости в СИ - сименс (См):
1 См - проводимость участка электрической цепи сопротивлением 1 Ом.
Величину, обратную удельному сопротивлению называют удельной электрической проводимостью.
Ее единица в СИ — сименс на метр (См/м). 1 См/м - удельная электрическая проводимость проводника, который при площади поперечного сечения 1 м2 и длине 1 м обладает электрической проводимостью 1 См.
Удельное сопротивление определяется химической природой вещества, а также температурой.
Как правило, ρ возрастает с температурой: в узких диапазонах изменения температуры удельное сопротивление металла описывается линейным законом:
ρ = ρ0 (1 + αT),
где ρ и ρ0 - соответственно удельные сопротив­ления проводника при T и О°С;
α - температурный коэффициент сопротивления, близкий при не очень низких температурах (273K)-1 .

Сопротивление многих металлов и сплавов (Al, Pb, Zn) при температурах Тк порядка (0,14—20К), скачкообразно уменьшается до нуля.Такие температуры называют критическими. При температуре ниже критической металл становится абсолютным проводником.
Впервые это явление, названное сверхпроводимостью,
обнаружено в 1911 г. Г. Камерлинг-Оннесом при охлаждении ртути ниже 4,2 К.
Al = 1,19К; Hg - 4,15К; Nb - 9,2К; V = 5,3К; V3Si = 17К.
В последнее время синтезированы и активно изучаются соединения
Bi—Sr—Ca—Си—О, которые переходят в сверхпроводящее состояние
при 110-125К.

На зависимости электрического сопротивления металлов от температуры основано действие термометров сопротивления
Сопротивление этих приборов очень остро реагирует на изменение температуры.
Это обстоятельство позволяет измерять температуру с точностью до 0,001 К.
Термометры сопротивления, в которых в качестве рабочего вещества используются полупроводники, называют термисторами.
Они позволяют измерять температуру с точностью до миллионных долей Кельвина.

Закон Ома для однородного участка цепи
Немецкий физик Георг Ом (1826) экспериментально установил, что сила тока, текущего по однородному металлическому проводнику, пропорциональна напряжению U на концах проводника и обратно пропорциональна сопротивлению R проводника:
-закон Ома для однородного участка цепи.
Напряжение U (в случае однородного проводника) совпадает с разностью потенциалов.

Найдем связь между векторами j (вектор плотности тока) и Е (напряженность поля) в одной и той же точке проводника. Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают
Напряжение, приложенное концам проводника, равно Edl, а его сопротивление
Подставив эти выражения в формулу
запишем
Ток I это суммарный ток через S - площадь поперечного сечения проводника. Тогда ток dI ток через элементарную площадку dS
.

Разделив левую и правую часть на dS, получим слева плотность тока.
или в векторном виде
Это выражение представляет собой закон Ома в дифференциальной форме для однородного участка цепи.
Этот закон связывает плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке.
Это соотношение справедливо и для переменных полей.

Чтобы перейти к интегральной форме закона Ома, рассмотрим случай, когда электрический ток течет вдоль тонких проводов. Тогда направление тока совпадает с направлением оси провода, и плотность тока j одинакова во всех точках сечения провода. Участок цепи 1-2 выбран произвольно, и в цепи имеется источник ЭДС.
Умножим слева и справа выражение
на элемент провода dl
затем разделив на γ,

проинтегрируем полученное выражение по длине провода от точки 1 до точки 2:
Левая часть этого уравнения
R12 сопротивление участке 1-2.
Получив выражение закона Ома, преобразуем правую часть.

правая часть
Первый интеграл в правой части уравнения
Второй интеграл
где ξ12 - ЭДС, действующая
на участке цепи 1-2
Это выражение представляет собой закон Ома для неоднородного участка цепи в интегральной форме. Это выражение также называют обобщенным законом Ома.

Если в цепи на участке 1-2 отсутствует источник, то ξ равно нулю
Выражение
приобретает вид :
Если цепь замкнута, выбранные точки 1 и 2 совпадают и ϕ1 = ϕ2,

В общем случае R = r + R1
r — внутреннее сопротивление источника ЭДС
R1 – полное сопротивление «внешних» (не источника ЭДС) элементов цепи.
Закон Ома для замкнутой цепи будет иметь вид
Если цепь разомкнута и, следовательно, в ней ток отсутствует ток (I = 0), то
ЭДС, действующая в разомкнутой цепи, равна разности потенциалов на ее концах. Чтобы найти ЭДС источника тока, надо измерить разность потенциалов на его клеммах при разомкнутой цепи.

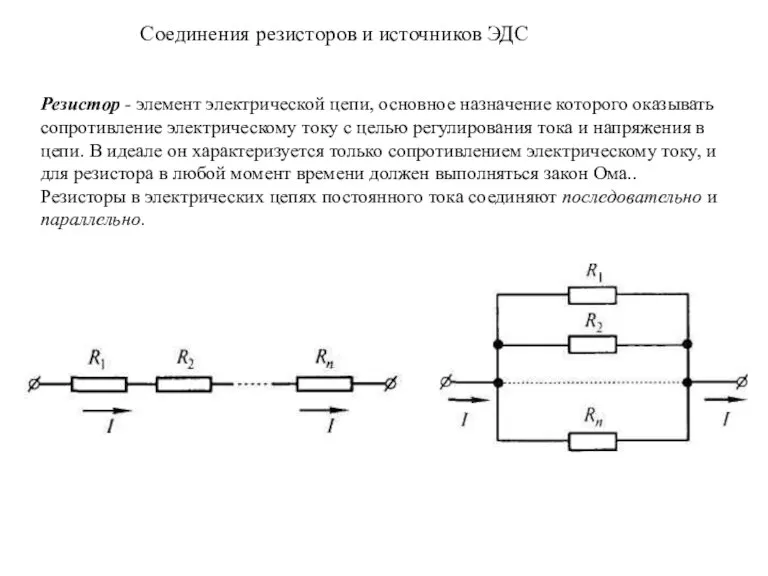
Соединения резисторов и источников ЭДС
Резистор - элемент электрической цепи, основное назначение которого оказывать сопротивление электрическому току с целью регулирования тока и напряжения в цепи. В идеале он характеризуется только сопротивлением электрическому току, и для резистора в любой момент времени должен выполняться закон Ома..
Резисторы в электрических цепях постоянного тока соединяют последовательно и параллельно.

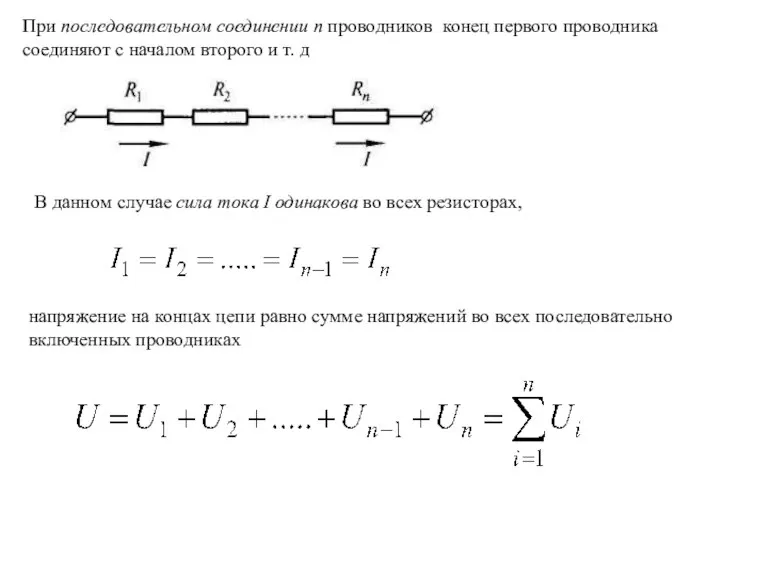
напряжение на концах цепи равно сумме напряжений во всех последовательно включенных проводниках
В данном случае сила тока I одинакова во всех резисторах,
При последовательном соединении п проводников конец первого проводника соединяют с началом второго и т. д

Найдем правило сложения сопротивлений, для этого запишем закон Ома для участка цепи
Полное сопротивление цепи
равно сумме сопротивлений последовательно соединенных резисторов.

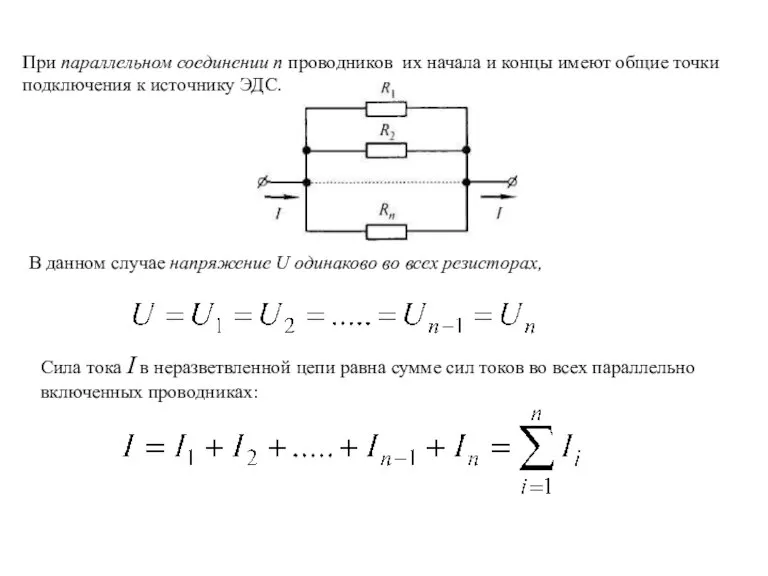
При параллельном соединении п проводников их начала и концы имеют общие точки подключения к источнику ЭДС.
В данном случае напряжение U одинаково во всех резисторах,
Cила тока I в неразветвленной цепи равна сумме сил токов во всех параллельно включенных проводниках:

Найдем правило сложения сопротивлений, для этого запишем закон Ома для участка цепи
Найдем правило сложения сопротивлений, для этого запишем закон Ома для участка
Величина, обратная полному сопротивлению цепи, равна сумме величин, обратных сопротивлениям всех параллельно соединенных резисторов.
Общее сопротивление, при параллельном соединении резисторов, всегда меньше сопротивления любого из них.
Часто используют и смешанное сопротивление резисторов.

Соединение последовательное и параллельное источников
Для варьирования напряжения во внешней цепи применяют последовательное соединение источников ЭДС.
Параллельное соединение источников тоже применяют, но с другой целью. Если требуется достичь больших значений силы тока в цепи нагрузки (например, большой мотор), мощности одного источника может не хватить. Тогда, применяют несколько одинаковых источников соединенных параллельно.
Применение источников с разным значением ЭДС возможно, но затруднительно.
Если применить источники с разным значением ЭДС то, напряжение на концах такой батареи будет равно ЭДС наибольшего источника. Это означает, что основной ток пойдет через него. Но его мощности может не хватить. И смысл использования батареи потеряется.
Вот почему параллельное включение используется только в случаях равных значений ЭДС. Применяется также смешанное включение источников.

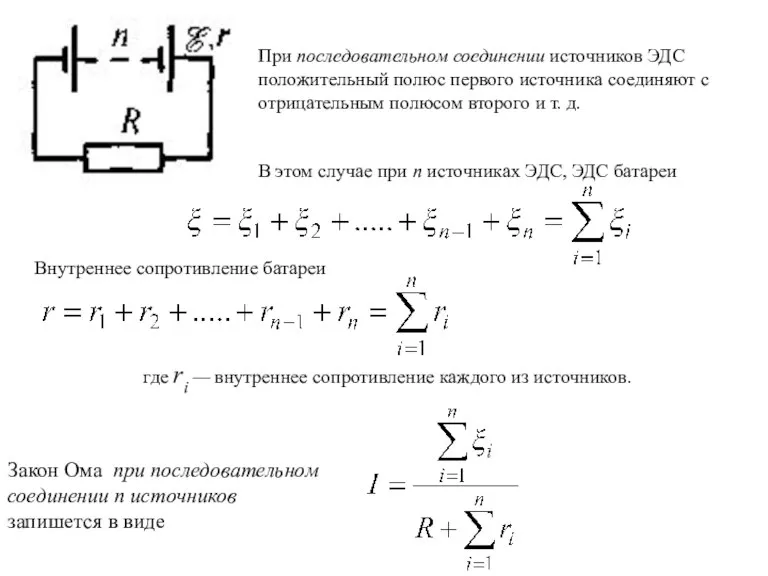
При последовательном соединении источников ЭДС положительный полюс первого источника соединяют с отрицательным полюсом второго и т. д.
В этом случае при п источниках ЭДС, ЭДС батареи
Внутреннее сопротивление батареи
где ri — внутреннее сопротивление каждого из источников.
Закон Ома при последовательном соединении п источников запишется в виде

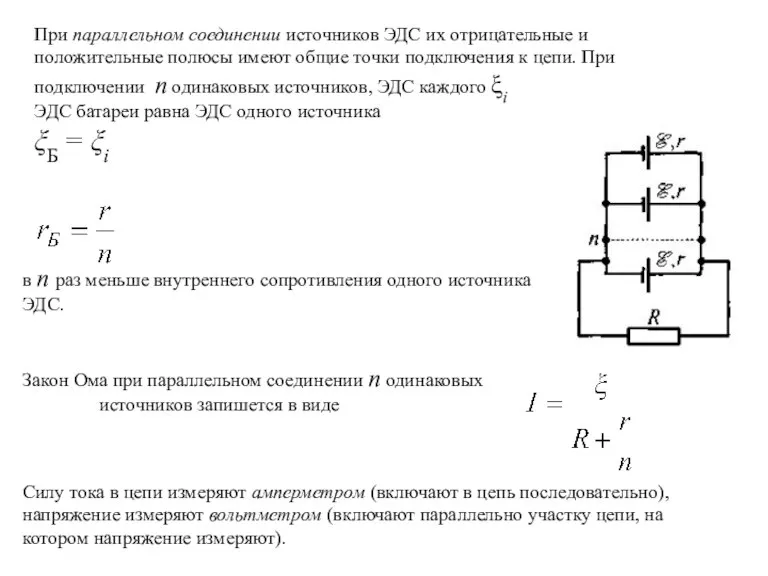
При параллельном соединении источников ЭДС их отрицательные и положительные полюсы имеют общие точки подключения к цепи. При подключении п одинаковых источников, ЭДС каждого ξi
ЭДС батареи равна ЭДС одного источника
ξБ = ξi
в п раз меньше внутреннего сопротивления одного источника ЭДС.
Закон Ома при параллельном соединении п одинаковых источников запишется в виде
Силу тока в цепи измеряют амперметром (включают в цепь последовательно), напряжение измеряют вольтметром (включают параллельно участку цепи, на котором напряжение измеряют).

Мощность тока. Закон Джоуля-Ленца
Рассмотрим однородный участок цепи, к концам которого приложено напряжение U. За время dt через сечение проводника переносится заряд dq.
dq = Idt
При этом силы электростатического поля и сторонние силы совершают работу
dA = Udq = UIdt
Если сопротивление проводника R, то, используя закон Ома, получим, что
работа
Мощность тока
Единицы работы и мощности тока в СИ - соответственно Джоуль и Ватт. На практике применяются также внесистемные единицы работы тока: ватт-час (Вт×ч), киловатт-час (кВт×ч);
1 Вт×ч это работа тока мощностью 1 Вт в течение 1 ч;
1 Вт×ч = 3600 Вт×с = 3,6×103 Дж; 1 кВт×ч = 3600 кДж.

Если ток проходит по неподвижному металлическому проводнику и в проводнике не происходит химических превращений, то работа dA идет только
на его нагревание dΘ = CdT,
dΘ = dA.
Тогда можем записать
Закон Джоуля-Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э.Х. Ленцем.
В случае, если сила тока изменяется со временем, количество теплоты Θ, выделяющееся за время t
Выделим в проводнике элементарный цилиндрический объем
dV= dSdl
ось цилиндра совпадает с направлением тока, сопротивление цилиндра