Содержание
- 2. Замечательные кривые Зовут меня ученые - кривая. Я - линия довольно не простая: Есть у меня
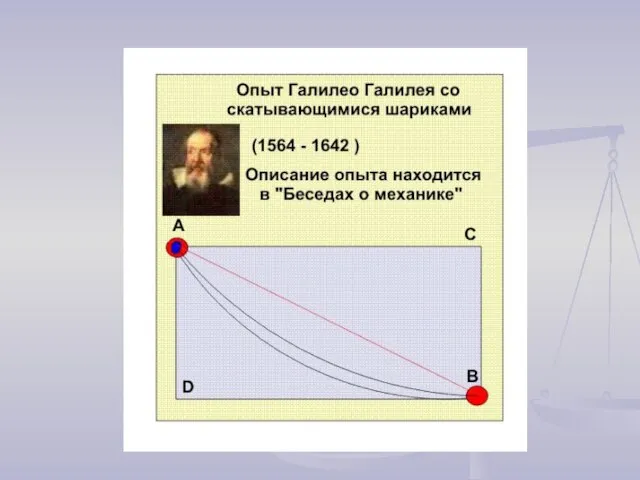
- 3. Циклоида Кривая, которую описывает точка, закрепленная на окружности, катящейся без скольжения по прямой линии, называется циклоидой.
- 8. Последовательное построение циклоиды Построение циклоиды производится в следующей последовательности: На направляющей горизонтальной прямой откладывают отрезок АА12,
- 9. Задачи на применение полученных знаний 1. Имеет ли циклоида: а) оси симметрии; б) центр симметрии? 2.
- 11. Скачать презентацию
Слайд 2Замечательные кривые
Зовут меня ученые - кривая.
Я - линия довольно не простая:
Есть у
Замечательные кривые
Зовут меня ученые - кривая.
Я - линия довольно не простая:
Есть у

И есть прямые слуги асимптоты.
Прямая ломит напролом, ломая шею.
Я ж обойти преграды все сумею,
А максимум и минимум известны
Кривую делает особо интересной
И как не хорохорится прямая,
Довольно точна линия такая
Представит синусоиду простую,
Взять только амплитуду нулевую.
И коль соображаешь ты, братишка,
Тогда при мне не задавайся слишком
Ведь знают все детсадовцы любые,
Что в голове извилины кривые!
Но, между прочим, и для разгильдяя
Живет во мне надежда неплохая:
Лентяй из двоек вылезет,
Когда «кривая вывезет».
Слайд 3Циклоида
Кривая, которую описывает точка, закрепленная на окружности, катящейся без скольжения по
Циклоида
Кривая, которую описывает точка, закрепленная на окружности, катящейся без скольжения по

Слайд 8Последовательное построение циклоиды
Построение циклоиды производится в следующей последовательности:
На направляющей горизонтальной прямой
Последовательное построение циклоиды
Построение циклоиды производится в следующей последовательности:
На направляющей горизонтальной прямой

Строят производящую окружность радиуса r, так чтобы направляющая прямая была касательной к неё в точке А;
Окружность и отрезок АА12 делят на несколько равных частей, например на 12;
Из точек делений 11, 21, ...121 восстанавливают перпендикуляры до пересечения с продолжением горизонтальной оси окружности в точках 01, 02, ...012;
Из точек деления окружности 1, 2, ...12 проводят горизонтальные прямые, на которых делают засечки дугами окружности радиуса r;
Полученные точки А1, А2, ...А12 принадлежат циклоиде.
Построение циклоиды производится в следующей последовательности:
На направляющей горизонтальной прямой откладывают отрезок АА12, равный длине производящей окружности радиуса r, (2pr);
Строят производящую окружность радиуса r, так чтобы направляющая прямая была касательной к неё в точке А;
Окружность и отрезок АА12 делят на несколько равных частей, например на 12;
Из точек делений 11, 21, ...121 восстанавливают перпендикуляры до пересечения с продолжением горизонтальной оси окружности в точках 01, 02, ...012;
Из точек деления окружности 1, 2, ...12 проводят горизонтальные прямые, на которых делают засечки дугами окружности радиуса r;
Полученные точки А1, А2, ...А12 принадлежат циклоиде.
Слайд 9Задачи на применение полученных знаний
1. Имеет ли циклоида:
а) оси симметрии;
Задачи на применение полученных знаний
1. Имеет ли циклоида:
а) оси симметрии;

б) центр симметрии?
2. Предположим, что круг без скольжения катится по прямой. Как мы знаем, точки на его окружности будут описывать циклоиды.
Нарисуйте кривую, которую будет описывать:
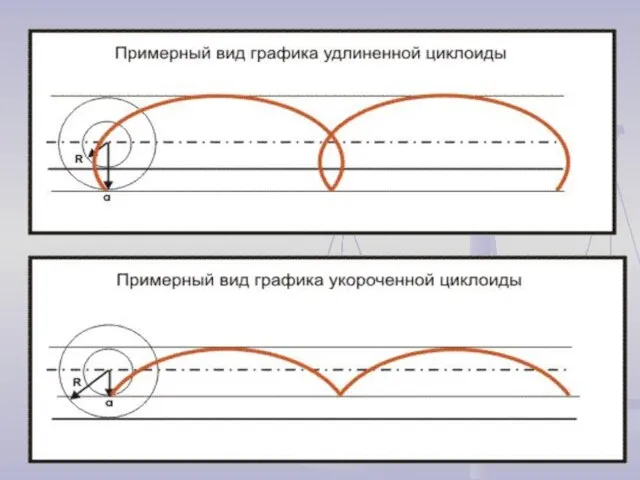
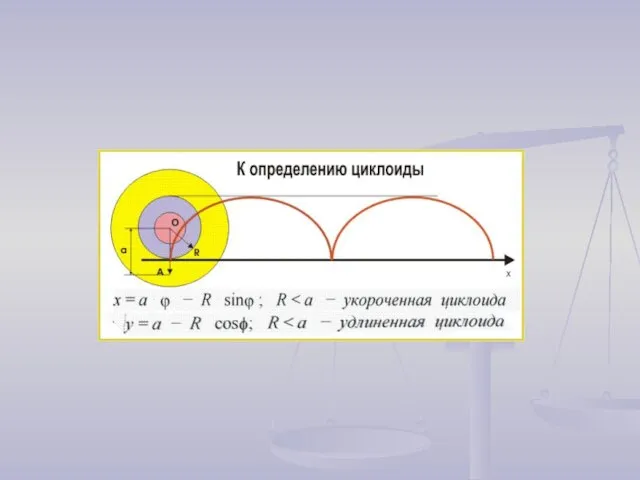
а) точка А, закрепленная внутри круга (укороченная циклоида);
б) точка В, закрепленная вне круга (удлиненная циклоида)
3. Нарисуйте траекторию движения вершины правильного n-угольника, катящегося по прямой аналогично окружности при: а) n = 3; б) n = 4; б) n = 6.
4. Докажите, что касательная к циклоиде перпендикулярна отрезку, соединяющему точку касания и точку соприкосновения окружности с прямой, по которой она катится.

 Алгоритм презентации на защиту
Алгоритм презентации на защиту Современная киноиндустрия
Современная киноиндустрия Кто придумал ноль ?
Кто придумал ноль ? Направления деятельности изостудии Росинка
Направления деятельности изостудии Росинка Объединение Мир искусства. Часть 3
Объединение Мир искусства. Часть 3 Адаптация профессиональных спортсменов к выполнению предусмотренных нагрузок
Адаптация профессиональных спортсменов к выполнению предусмотренных нагрузок es-Persona индивидуальные заказы
es-Persona индивидуальные заказы Основы графической грамоты. Трудовое обучение
Основы графической грамоты. Трудовое обучение Установка разделения изотопов бора методом экстрактивной ректификации
Установка разделения изотопов бора методом экстрактивной ректификации Оценка уровня развития базовых способностей обучающихся
Оценка уровня развития базовых способностей обучающихся Презентация на тему Занятие по профориентации «Профессия - ветеринар»
Презентация на тему Занятие по профориентации «Профессия - ветеринар» История про маленьких лягушат….
История про маленьких лягушат…. Очистка и дезинфекция медицинских инструментов.
Очистка и дезинфекция медицинских инструментов. Особенности кредитно-модульной организации учебного процесса
Особенности кредитно-модульной организации учебного процесса Современные PLC телекоммуникации
Современные PLC телекоммуникации Здоровьесберегающие образовательные технологии на уроках английского языка
Здоровьесберегающие образовательные технологии на уроках английского языка Результаты инновационной работы педагогов ДОУ, представленных в СМИ 2011г.
Результаты инновационной работы педагогов ДОУ, представленных в СМИ 2011г. «Стабильный успех»
«Стабильный успех» Технологические среды в микроэлектронике. Газоподготовка в электронной технике
Технологические среды в микроэлектронике. Газоподготовка в электронной технике Я через 15 лет
Я через 15 лет The Golden Age
The Golden Age Машинные швы
Машинные швы РазработкаГосударственной Стратегии по развитию рынка трудадо 2020 года.
РазработкаГосударственной Стратегии по развитию рынка трудадо 2020 года. Криптосистемы с открытым ключем
Криптосистемы с открытым ключем Экскурсия в город Мастеров и Мастериц
Экскурсия в город Мастеров и Мастериц Битва за Днепр
Битва за Днепр Насилие в произведениях искусства
Насилие в произведениях искусства Страховая Компания «Согласие» является одной из крупнейших отечественных компаний, успешно работающей на Российском рынке страх
Страховая Компания «Согласие» является одной из крупнейших отечественных компаний, успешно работающей на Российском рынке страх