Слайд 2Цели
1.Сформировать умение работать с законом сохранения массы.
2.Обеспечить усвоение обучающими понятий концентрации

вещества, процентного раствора.
3.Обобщить полученные знания при решении задач на проценты
Слайд 3При решении данного вида задач используются следующие допущения:
Всегда выполняется «Закон сохранения объёма

и массы»
Данный закон выполняется и для отдельных составляющих частей (компонентов) сплава (раствора)
При соединении растворов и сплавов не учитываются химические взаимодействия их отдельных компонентов.
Слайд 4Основные понятия
Смесь состоит из «чистого вещества» и «примеси».
Долей а чистого вещества и

смеси называется отношение количества чистого вещества m в смеси к общему количеству М смеси при условии, что они измерены одной и той же единицей массы и объёма: а=m/М.
Процентным содержанием чистого вещества в смеси с называют его долю, выраженную процентным отношением: с=а 100%.
Формула для расчёта концентрации смесей (сплавов): n=mb/mp
Слайд 5Задача 1
Сколько граммов воды надо добавить к 50г раствора, содержащего 8

% соли, чтобы получить 5% раствора
Слайд 6Решение
Пусть Х -количество воды, которое надо добавить. Новое количество раствора -

(50 + Х) г. Количество соли в исходном растворе 50 •0,08 г. Количество соли в новом растворе составляет 5 % от (50 + Х) г, т. е. 0,05(50 + Х) г.
Так как количество соли от добавления воды не изменилось, то оно одинаково в исходном и новом растворах. Получаем уравнение. Иногда в химии это уравнение называют кратко «баланс по соли».
50•0,08 = 0,05(50 + Х),
50•8 = 5(50 +Х),
80 = 50 +Х,
Х=30
Ответ: 30 г.
Слайд 7Задача 2
Сколько граммов 30% раствора надо добавить к 80г 12% раствора

этой же соли, чтобы получить 20 % раствор соли?
Слайд 8Решение задачи 2
Пусть надо добавить Х г 30 % раствора соли.

Получится
(80 + Х) г 20 % раствора. В 80 г 12 % раствора содержится 80•0,12 г соли 0,ЗХг соли — в Х г 30 % раствора, 0,2(80 + Х) г соли — в (80 + Х) г 20 % раствора.
Получаем уравнение:
0,Зх + 0,12•80 = 0,2(80 + Х) — это и есть «баланс по соли».
0,ЗХ+9,6 =16+0,2Х,
0,ЗХ—0,2Х= 16—9,6,
0,IХ = 6,4,
Х=64.
Ответ: 64 г.
Слайд 9Задача 3
Если смешать 8 кг и 2 кг растворов серной кислоты

разной
концентрации, то получим 12 %-й раствор кислоты. При смешивании
двух одинаковых масс тех же растворов получим 15 %-й раствор.
Определите первоначальную концентрацию каждого раствора
Слайд 10Решение задачи 3
Пусть концентрация серной кислоты в первом растворе Х%, а

во втором
растворе —У%. Это значит, что в 1 кг первого раствора содержится Х/100 кг кислоты и 1-Х/100 кг воды, тогда в 8 кг первого раствора 8Х /100 кг кислоты и (8-8Х/100)кг воды.
Во втором растворе аналогично: У/100кг кислоты; (1-У/100) кг воды, в 2кг- 2У/100кг кислоты и (2- 2У/100) кг воды.
После смешения получим раствор общей массой 10 кг, в нем содержится (8Х/100+2У/100) кг кислоты. По условию получаем раствор
12 %-и концентрации, значит, в 10 кг раствора будет 10• 12/100кг кислоты
Получаем уравнение 8Х/100+2У/100=1,2. Преобразуя, получим 4х + у = 60 — первое уравнение системы.
Рассмотрим вторую ситуацию. Пусть возьмем по 1 кг каждого
раствора, тогда будет Х/100 кг кислоты, а в 1 кг второго раствора содержится У/100кг кислоты. Так как смесь получится 15 %-й концентрации, то в (1 + 1) кг смеси должно содержаться 2*15/100 =0,3 кг кислоты.
Получаем второе уравнение Х/100+У/100=0,3, после преобразований имеем Х+ У= 30.
Решив систему уравнений, получим Х=10, У=20.
Ответ: 10 %-й и. 20 %й растворы.
Слайд 11Задача 4
Имеется два куска сплава олова и свинца, содержащие 60 %

и 40% олова. По сколько граммов от каждого куска надо взять, чтобы получить 600 г сплава, содержащего 45 % олова?
Слайд 12Решение задачи 4
Пусть масса куска, взятого от первого сплава т1 г,

тогда масса куска от второго сплава будет 600 - т1, составим уравнение
т1•0,6 +(б00— т1)•0,4= 600•0,45,
6 т1+2400—4 т1 =2700,
20 т1 = 3000,
т1 = 150,
600— т1 =450,
т2=450.
Ответ: I50г;450г.











 Сервис Мечты
Сервис Мечты Основи формування і реєстраціi корисного сигналу в діапазоні
Основи формування і реєстраціi корисного сигналу в діапазоні Комплексная система автоматизации
Комплексная система автоматизации Телепорт
Телепорт Осторожно! Сосульки
Осторожно! Сосульки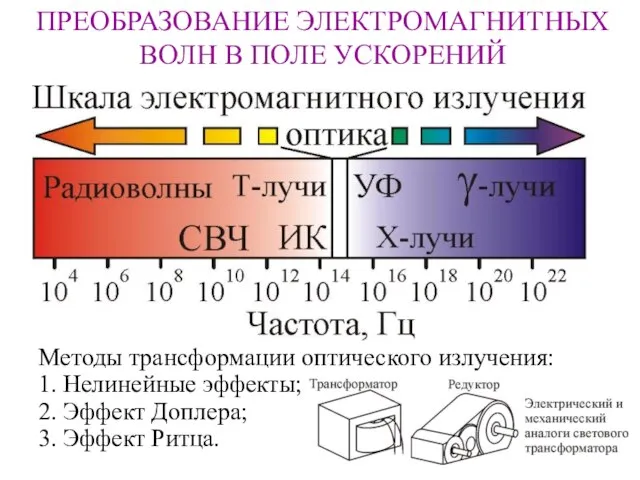 ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ
ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ Примеры комбинаторных задач (9 класс)
Примеры комбинаторных задач (9 класс) Решение логических задач из курса кибернетики
Решение логических задач из курса кибернетики Бедность
Бедность Nocturnal eczema: Review of sleep and circadian rhythms
Nocturnal eczema: Review of sleep and circadian rhythms Microsoft Office Word 2007
Microsoft Office Word 2007 Международное сотрудничество в освоении космического пространства
Международное сотрудничество в освоении космического пространства Золото
Золото Презентация на тему Загадки о диких животных
Презентация на тему Загадки о диких животных Королева оркестра
Королева оркестра Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина
Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар
Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар Образ Чичикова в поэме "Мертвые души"
Образ Чичикова в поэме "Мертвые души" Табір "Світанок"
Табір "Світанок" Презентация на тему Уфа – столица Башкортостана
Презентация на тему Уфа – столица Башкортостана Онтология
Онтология  Источники загрязнения окружающей среды
Источники загрязнения окружающей среды Project_A
Project_A Типы связи слов в словосочетании
Типы связи слов в словосочетании Всероссийский флешмоб Голубь мира
Всероссийский флешмоб Голубь мира Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во
Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во БИОСИНТЕЗ
БИОСИНТЕЗ Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12
Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12