Содержание
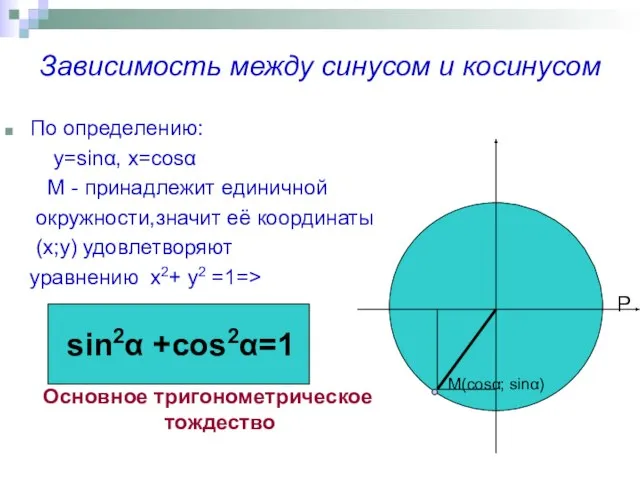
- 2. Зависимость между синусом и косинусом По определению: y=sinα, x=cosα М - принадлежит единичной окружности,значит её координаты
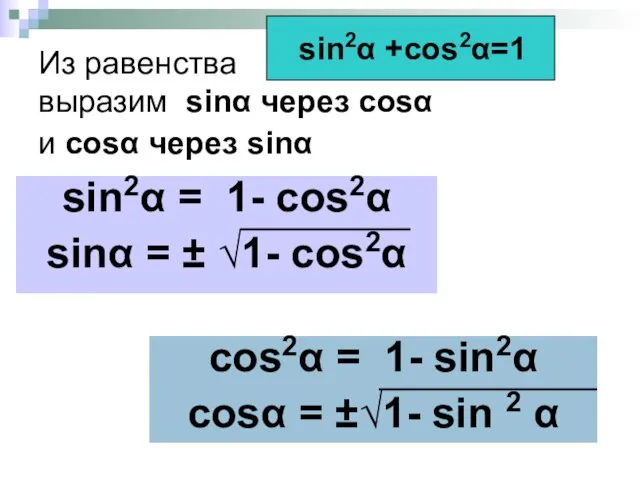
- 3. Из равенства выразим sinα через cosα и cosα через sinα sin2α = 1- cos2α sinα =
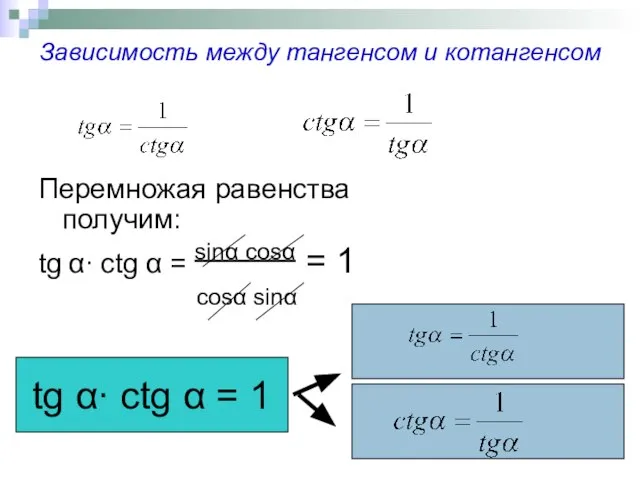
- 5. Зависимость между тангенсом и котангенсом Перемножая равенства получим: tg α∙ сtg α = sinα cosα =
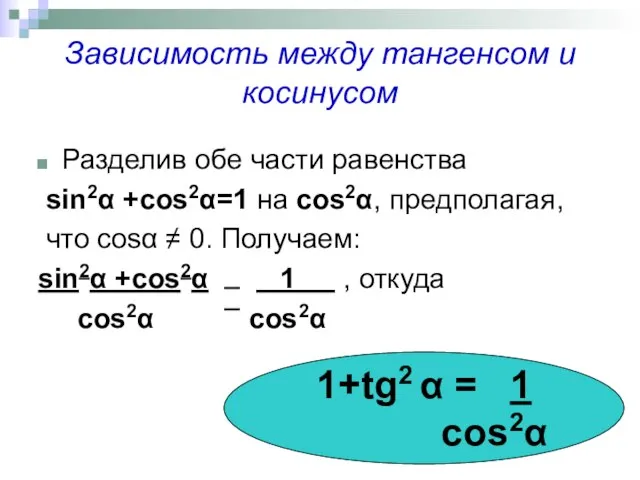
- 6. Зависимость между тангенсом и косинусом Разделив обе части равенства sin2α +cos2α=1 на cos2α, предполагая, что cosα
- 7. №2. Вычислить tgα ,если cosα = – 3/5 и п/2 Из формулы Получаем: tg2α = 1
- 8. В классе: № 457(1,3) № 458(1)
- 10. Скачать презентацию



 Презентация на тему Задачи на смеси и сплавы (9 класс)
Презентация на тему Задачи на смеси и сплавы (9 класс) Русская литература XX века: общая характеристика
Русская литература XX века: общая характеристика Денежные единицы мира
Денежные единицы мира Презентация на тему Золотой век Екатерины II
Презентация на тему Золотой век Екатерины II  Доходный подход к оценке
Доходный подход к оценке Музей Конфлуанс
Музей Конфлуанс Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ
Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ Презентация на тему Технология обработки древесины
Презентация на тему Технология обработки древесины Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье
Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье Поняття ЕТ Excel
Поняття ЕТ Excel Налоги: сущность и виды. Классификация
Налоги: сущность и виды. Классификация Внутреняя энергия
Внутреняя энергия В стране правовых знаний
В стране правовых знаний Убранство русской избы
Убранство русской избы Политико-правовая теория Монтескье
Политико-правовая теория Монтескье 169601
169601 Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол
Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол Франсуа Виет и его теорема (8 класс)
Франсуа Виет и его теорема (8 класс) Может ли природа жить без человека?
Может ли природа жить без человека? Юридическая ответственность и её виды
Юридическая ответственность и её виды Осенняя одежда
Осенняя одежда Банк внешней торговли (Внешторгбанк)
Банк внешней торговли (Внешторгбанк)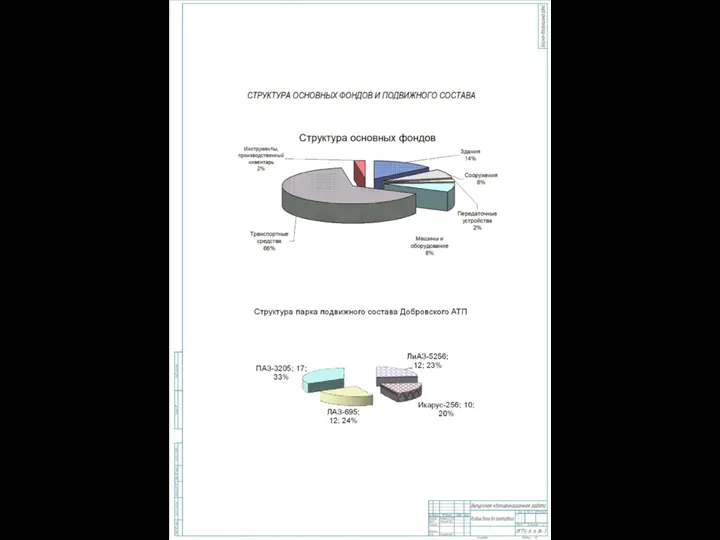 Структура основных фондов и подвижного состава
Структура основных фондов и подвижного состава Saint Isaac’s Square
Saint Isaac’s Square Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.
Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.  Педагогический совет
Педагогический совет Виды Смоленска
Виды Смоленска НАСС
НАСС