Знакомьтесь - параметры!

- Знакомство с параметрами.
ЦЕЛЬ УРОКА
- Рассмотреть различные способы решения задач с параметрами.

II. Объяснение нового материала в форме
лекции.
I. Организационный момент.
III. Решение задач с параметрами.
IV. Подведение итогов.
V. Домашнее задание.
Дерзай !!!
ПЛАН УРОКА

«Многие вещи нам не понятны не потому, что наши понятия слабы, но потому, что многие вещи не входят в круг наших понятий».
ЭПИГРАФ К УРОКУ
«Параметры – это сложно, но важно для вас»!

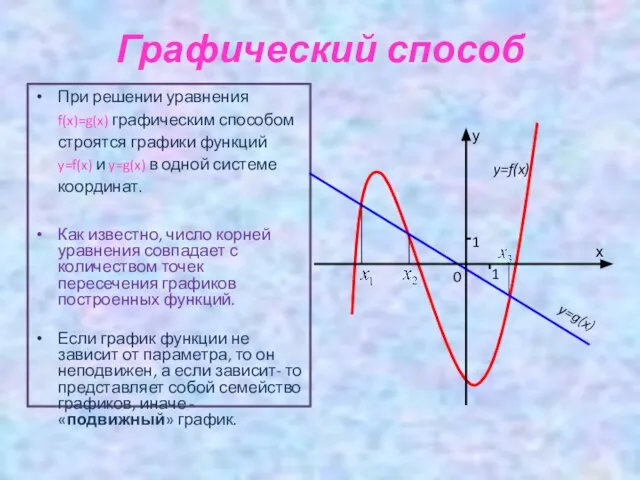
Графический способ
При решении уравнения f(x)=g(x) графическим способом строятся графики функций y=f(x) и y=g(x) в одной системе координат.
Как известно, число корней уравнения совпадает с количеством точек пересечения графиков построенных функций.
Если график функции не зависит от параметра, то он неподвижен, а если зависит- то представляет собой семейство графиков, иначе - «подвижный» график.
y=f(x)
y=g(x)

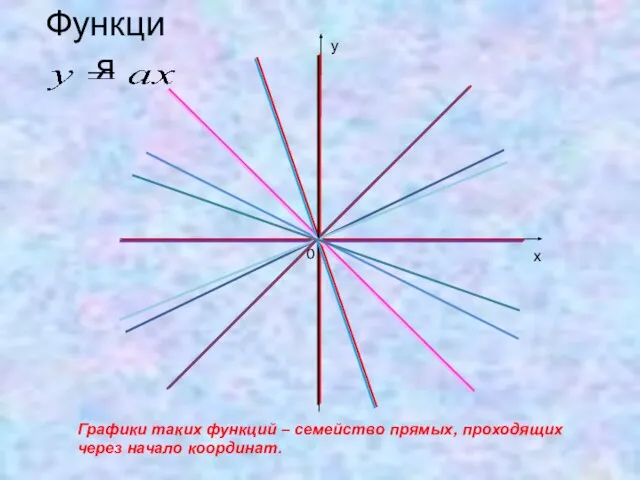
Функция
Графики таких функций – семейство прямых, проходящих
через начало координат.
х
у
0

2. Построим графики функции
и рассмотрим
различные случаи в зависимости
от параметра .
Задача. Сколько корней имеет уравнение
для каждого из значений параметра ?
Решение.
1. Построим график функции
Ответ:
1) При
уравнение имеет один корень
1
2
1
Нет корней
1
2) При
уравнение имеет два корня
3) При
уравнение не имеет корней

Задача. Решить уравнение
Решение.
Данное уравнение четвертой степени относительно переменной х и является квадратным относительно параметра .
а

Возможны различные случаи. Результаты
исследования этих случаев запишем в таблицу:
Ответ:
если а<-1, то действительных корней нет;
если а = -1, то
если -1
если а=1, то
если а>1, то

При каких значениях параметра P функция определена при всех хєR ?
Решение.
Область определения функции - множество действительных
чисел, удовлетворяющих условию:
Какие условия должны выполняться, чтобы решением этого неравенства являлась вся числовая прямая?
Ответ:(-∞ ; -1].