Золотое сечение в архитектуре

Содержание
Понятие «золотого сечения»
«Золотое сечение» отрезка
«Золотой» прямоугольник
«Золотой» треугольник
Пятиконечная звезда
«Золотое сечение» в анатомии
«Золотое сечение» в скульптуре
«Золотое сечение» в современной архитектуре
«Золотое сечение» в древней архитектуре

Золотое сечение
Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему отрезку. Соотношение это примерно равно 0,618.
a : b = b : c или с : b = b : а.
Формула

«Золотое сечение» отрезка
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Свойства золотого сечения описываются
уравнением: x*х – x – 1 = 0.
Решение этого уравнения:

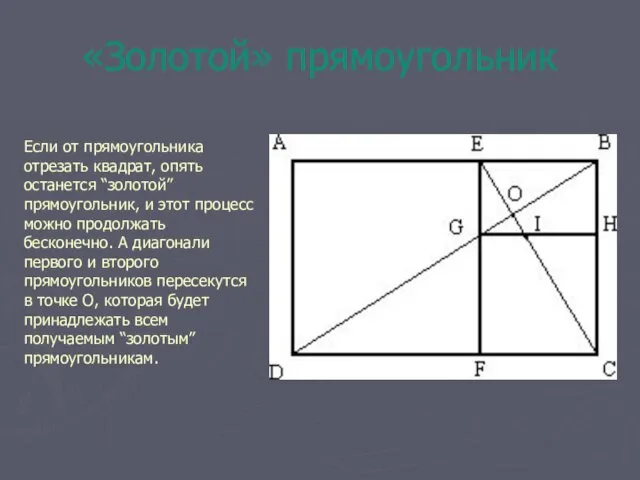
«Золотой» прямоугольник
Если от прямоугольника отрезать квадрат, опять останется “золотой” прямоугольник, и этот процесс можно продолжать бесконечно. А диагонали первого и второго прямоугольников пересекутся в точке О, которая будет принадлежать всем получаемым “золотым” прямоугольникам.

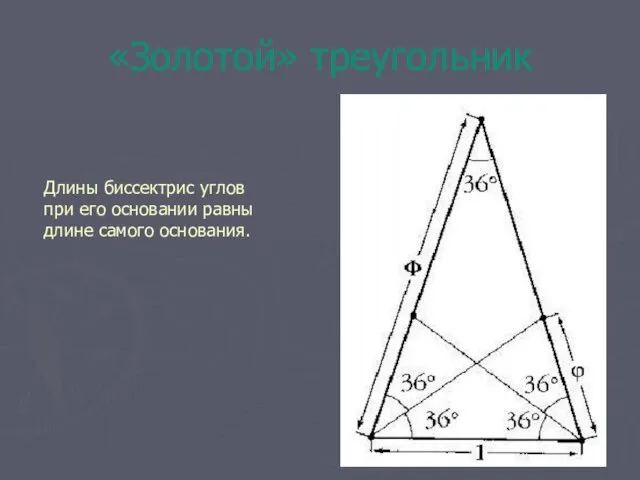
«Золотой» треугольник
Длины биссектрис углов при его основании равны длине самого основания.

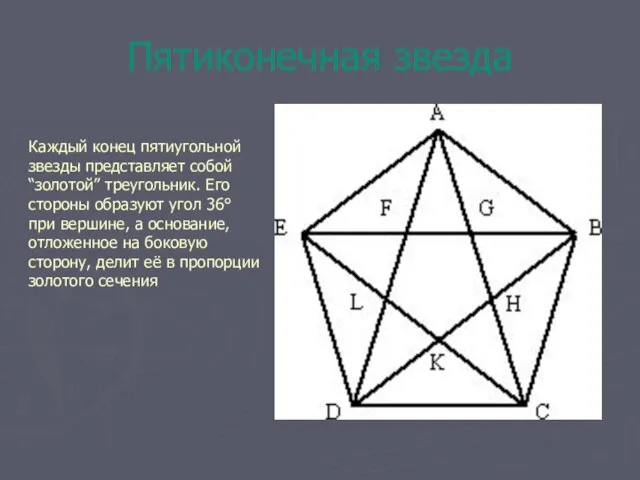
Пятиконечная звезда
Каждый конец пятиугольной звезды представляет собой “золотой” треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит её в пропорции золотого сечения

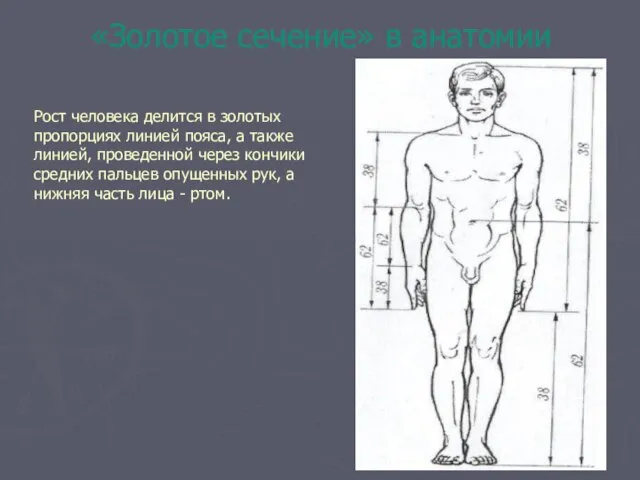
«Золотое сечение» в анатомии
Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, а нижняя часть лица - ртом.

«Золотое сечение» в скульптуре
Золотая пропорция статуи Аполлона: рост изображенного человека делится пупочной линией в золотом сечении.

Дорифор Поликлета
Венера Милосская

«Золотое сечение» в современной архитектуре
Пропорции Покровского собора на Красной площади в Москве определяются восемью членами ряда золотого сечения. Многие члены этого ряда повторяются в затейливых элементах храма многократно.

«Золотое сечение» в древней архитектуре
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по золотому сечению, то получим те или иные выступы фасада.

В здании собора Парижской Богоматери мы тоже видим золотую пропорцию.