Содержание
- 2. Зонная модель электронной проводимости металлов Согласно квантовым представлениям, энергия электронов в атоме может изменяться дискретным образом.
- 3. Зонная модель электронной проводимости металлов Названы они так в честь итальянского физика Э. Ферми, впервые описавшего
- 4. Зонная модель электронной проводимости металлов В металлах внешние валентные оболочки заполнены не полностью, например, у атомов
- 5. Зонная модель электронной проводимости металлов Расстояние между соседними энергетическими уровнями очень мало, поскольку N очень велико
- 6. Зонная модель электронной проводимости металлов Однако эту проводимость обеспечивают не все свободные электроны металла, а лишь
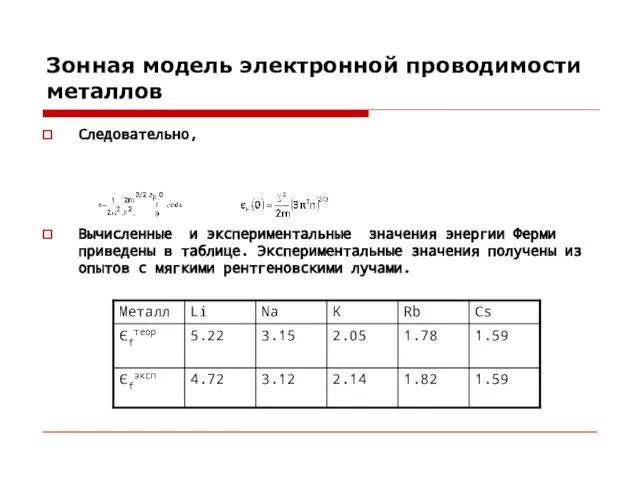
- 7. Зонная модель электронной проводимости металлов Следовательно, Вычисленные и экспериментальные значения энергии Ферми приведены в таблице. Экспериментальные
- 8. Зонная модель электронно-дырочной проводимости полупроводников При образовании твердых тел возможна ситуация, когда энергетическая зона, возникшая из
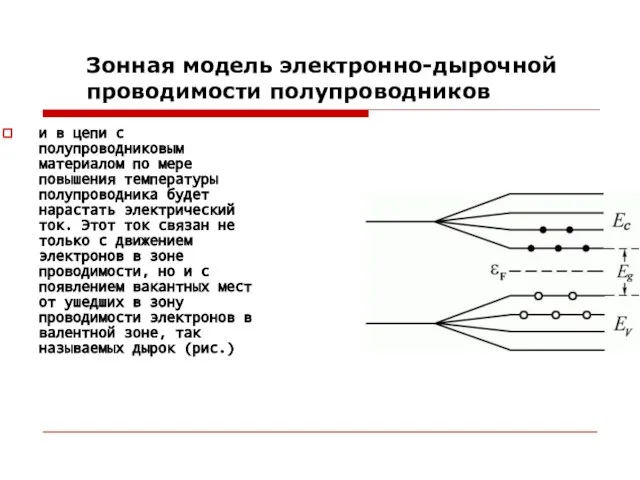
- 9. Зонная модель электронно-дырочной проводимости полупроводников и в цепи с полупроводниковым материалом по мере повышения температуры полупроводника
- 10. Зонная модель электронно-дырочной проводимости полупроводников В условиях термодинамического равновесия число электронов, переходящих в зону проводимости n
- 11. Зонная модель электронно-дырочной проводимости полупроводников Электроны забрасываются в зону проводимости с уровня Ферми, который оказывается в
- 12. Зонная модель электронно-дырочной проводимости полупроводников Если ввести в кремний атомы трехвалентного элемента, допустим атомы бора, то
- 13. Зонная модель электронно-дырочной проводимости полупроводников Концентрацию ионизованной примеси можно также рассчитать из условия равновесия между процессами
- 14. Зонная модель электронно-дырочной проводимости полупроводников
- 15. Электронно-дырочные переходы Рассмотрим контакт двух полупроводников с различными типами проводимости р- и n-типа. На практике такой
- 16. Электронно-дырочные переходы Поскольку в полупроводнике р-типа избыток положительно заряженных дырок, а в n-типа – электронов, то
- 17. Электронно-дырочные переходы Если изменить направление внешнего электрического поля и направить его от р- к n-области, против
- 18. Электронно-дырочные переходы Полупроводниковые выпрямители весьма компактны и обладают высоким КПД. Так, выпрямитель на основе Ge с
- 19. Сверхпроводимость Существует одно явление, механизм которого оказалось возможным объяснить лишь в рамках квантовой теории. Причем между
- 20. Сверхпроводимость В 1957 г. Дж. Бардином, Л. Купером, Дж. Шрифером дано квантово-механическое объяснение природы сверхпроводимости (теория
- 21. Сверхпроводимость Поскольку силы притяжения невелики, спаренные электроны слабо локализованы в пространстве. Эффективный диаметр куперовской пары имеет
- 23. Скачать презентацию
Слайд 2Зонная модель электронной проводимости металлов
Согласно квантовым представлениям, энергия электронов в атоме может
Зонная модель электронной проводимости металлов
Согласно квантовым представлениям, энергия электронов в атоме может

Слайд 3Зонная модель электронной проводимости металлов
Названы они так в честь итальянского физика Э.
Зонная модель электронной проводимости металлов
Названы они так в честь итальянского физика Э.

При сближении большого числа атомов в пределах твердого тела происходит расщепление исходного энергетического уровня валентного электрона в атоме на N подуровней в твердом теле, где N − число атомов, образующих кристалл. В результате образуется зона разрешенных энергетических уровней для электронов в твердом теле (рис.1).
Слайд 4Зонная модель электронной проводимости металлов
В металлах внешние валентные оболочки заполнены не полностью,
Зонная модель электронной проводимости металлов
В металлах внешние валентные оболочки заполнены не полностью,

При сближении N атомов Ag и расщеплении внешнего энергетического уровня 5s1 на N подуровней каждый из них заполняется уже двумя электронами с различными ориентациями спинов, что показано стрелками на рис. 1. В результате при сближении N атомов серебра возникает энергетическая зона, наполовину заполненная электронами.
Энергия, соответствующая последнему заполненному электронному уровню при 0 К, называется энергией Ферми εF ≈ kTg.
Слайд 5Зонная модель электронной проводимости металлов
Расстояние между соседними энергетическими уровнями очень мало, поскольку
Зонная модель электронной проводимости металлов
Расстояние между соседними энергетическими уровнями очень мало, поскольку

Слайд 6Зонная модель электронной проводимости металлов
Однако эту проводимость обеспечивают не все свободные электроны
Зонная модель электронной проводимости металлов
Однако эту проводимость обеспечивают не все свободные электроны

Концентрация таких электронов примерно равна nT/Tg, где Tg = 5⋅104 К – температура вырождения.
Пусть n − число всех электронов на единицу объема металла:
N(ε) –функция плотности состояний; N(ε)dε − число электронов в единице объема, приходящееся на интервал энергий от ε до ε + dε.
При абсолютном нуле все уровни энергии до εF включительно заняты двумя электронами каждый, а все уровни выше εF свободны. Для функции плотности состояний имеем
Слайд 7Зонная модель электронной проводимости металлов
Следовательно,
Вычисленные и экспериментальные значения энергии Ферми приведены в
Зонная модель электронной проводимости металлов
Следовательно,
Вычисленные и экспериментальные значения энергии Ферми приведены в
Слайд 8Зонная модель электронно-дырочной проводимости полупроводников
При образовании твердых тел возможна ситуация, когда энергетическая
Зонная модель электронно-дырочной проводимости полупроводников
При образовании твердых тел возможна ситуация, когда энергетическая

При повышении температуры полупроводников и диэлектриков электроны способны получать дополнительную энергию, связанную с тепловым движением kT. У части электронов энергии теплового движения оказывается достаточно для перехода из валентной зоны в зону проводимости, где электроны под действием внешнего электрического поля могут перемещаться практически свободно
и в цепи с полупроводнико
Слайд 9Зонная модель электронно-дырочной проводимости полупроводников
и в цепи с полупроводниковым материалом по мере
Зонная модель электронно-дырочной проводимости полупроводников
и в цепи с полупроводниковым материалом по мере
Слайд 10Зонная модель электронно-дырочной проводимости полупроводников
В условиях термодинамического равновесия число электронов, переходящих в
Зонная модель электронно-дырочной проводимости полупроводников
В условиях термодинамического равновесия число электронов, переходящих в

n ~ , должно равняться числу электронов n, рекомбинирующих с дырками р в валентной зоне Bnp:
Bnp =
Если полупроводник не содержит каких-либо примесей – собственный полупроводник, то n ≈ p и мы получаем
n =
Слайд 11Зонная модель электронно-дырочной проводимости полупроводников
Электроны забрасываются в зону проводимости с уровня Ферми,
Зонная модель электронно-дырочной проводимости полупроводников
Электроны забрасываются в зону проводимости с уровня Ферми,

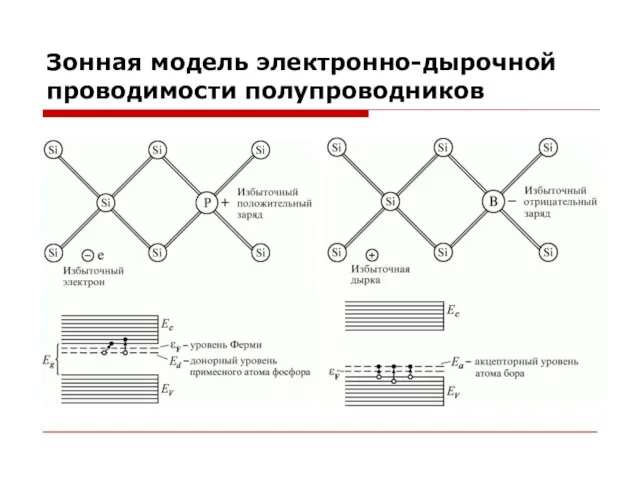
Существенно изменить проводимость полупроводников можно, введя в них очень небольшие количества примесей. Так, добавление в чистый кремний 10−3 % (атом/атом) атомов фосфора увеличивает электропроводность кристалла в 105 раз. В металлах примесь всегда уменьшает проводимость. Небольшое добавление примеси к полупроводнику называется легированием. Если добавить пятивалентный атом фосфора в решетку кремния, то четыре валентных электрона фосфора вступят в связь с четырьмя соседними атомами кремния, у которого во внешней оболочке четыре электрона, а пятый электрон атома Р может достаточно легко отщепиться в результате теплового движения и перейти в зону проводимости (рис. 6.11).
В зонной диаграмме атомы Р образуют систему энергетических уровней, расположенных вблизи дна зоны проводимости – донорные уровни (от лат. dono – дарю), с которых электроны могут достаточно легко переходить в зону проводимости, существенно увеличивая проводимость полупроводника. Полупроводники, легированные донорной примесью, называются полупроводниками n-типа (n – negative – отрицательный). За проводимость таких полупроводников отвечают свободные электроны, заряженные отрицательно.
Слайд 12Зонная модель электронно-дырочной проводимости полупроводников
Если ввести в кремний атомы трехвалентного элемента, допустим
Зонная модель электронно-дырочной проводимости полупроводников
Если ввести в кремний атомы трехвалентного элемента, допустим

Слайд 13Зонная модель электронно-дырочной проводимости полупроводников
Концентрацию ионизованной примеси можно также рассчитать из условия
Зонная модель электронно-дырочной проводимости полупроводников
Концентрацию ионизованной примеси можно также рассчитать из условия

Nd+ имеем
где А, В – коэффициенты; n – концентрация электронов в зоне проводимости; Nd >>Nd+ , Nd – концентрация неионизованных примесных атомов; Еd – глубина залегания донорной примеси под дном зоны проводимости. Поскольку n ≈ Nd+, то получаем
n≈
Ионизация примесей идет с уровня Ферми, который в легированном донорами полупроводнике расположен посередине между уровнем примеси и дном зоны проводимости.
Слайд 14Зонная модель электронно-дырочной проводимости полупроводников
Зонная модель электронно-дырочной проводимости полупроводников
Слайд 15Электронно-дырочные переходы
Рассмотрим контакт двух полупроводников с различными типами проводимости р- и n-типа.
Электронно-дырочные переходы
Рассмотрим контакт двух полупроводников с различными типами проводимости р- и n-типа.

Рис. 6.13. Принципиальная схема контакта двух полупроводников с проводимостью р- и n-типа (а). Распределение электронов и дырок в области p-n перехода (б). Изменение электрического потенциала в p-n переходе (в). Вольт-амперная характеристика p-n перехода (г)
Слайд 16Электронно-дырочные переходы
Поскольку в полупроводнике р-типа избыток положительно заряженных дырок, а в n-типа
Электронно-дырочные переходы
Поскольку в полупроводнике р-типа избыток положительно заряженных дырок, а в n-типа

Слайд 17Электронно-дырочные переходы
Если изменить направление внешнего электрического поля и направить его от р-
Электронно-дырочные переходы
Если изменить направление внешнего электрического поля и направить его от р-

Поэтому если включить p-n переход в цепь с напряжением, изменяющим свой знак, то при одном направлении поля ток через контакт будет проходить, а при другом – нет. В такой цепи произойдет выпрямление напряжения. На этом принципе работают полупроводниковые выпрямители (рис.).
«Выпрямление» напряжения p-n переходом (полупроводниковым диодом). На выходе получается постоянное по знаку пульсирующее напряжение
Слайд 18Электронно-дырочные переходы
Полупроводниковые выпрямители весьма компактны и обладают высоким КПД. Так, выпрямитель на
Электронно-дырочные переходы
Полупроводниковые выпрямители весьма компактны и обладают высоким КПД. Так, выпрямитель на

Если концы кристалла с p-n переходом подключить к микроамперметру и осветить область p-n перехода фотонами с энергией hν > Eg – большей ширины запрещенной зоны, то по цепи пойдет ток и стрелка прибора отклонится. Поглощенные областью p-n перехода фотоны будут генерировать электроны и дырки. В области двойного электрического слоя электрон будет перемещаться в n-область, а дырка − в р-область. В результате ток потечет по внешней цепи из р-области в n-область. Энергия фотонов в области p-n перехода будет превращаться в электрическую энергию. На этом принципе работают солнечные батареи, которые превращают световое излучение Солнца в электроэнергию, например для питания приборов на космических кораблях
Слайд 19Сверхпроводимость
Существует одно явление, механизм которого оказалось возможным объяснить лишь в рамках квантовой
Сверхпроводимость
Существует одно явление, механизм которого оказалось возможным объяснить лишь в рамках квантовой

Изучая поведение сопротивления ртути, охлаждаемой до гелиевых температур, Камерлинг-Оннес в 1911 г. впервые в мире наблюдал исчезновение сопротивления ртути практически до нуля. Это явление было названо сверхпроводимостью. Камерлинг-Оннес писал: «При 4,3 К сопротивление ртути уменьшается до 0,084 Ом, что составляет 0,0021 от значения сопротивления, которое имела бы твердая ртуть при 0 °С (39,7 Ом). Обнаружено, что при 3 К сопротивление падает ниже 3⋅10-6 Ом, что составляет 10-7 от значения при 0 °С». Отметим, что температурный интервал, в котором сопротивление уменьшалось до нуля, очень узок, и для некоторых металлов он составляет лишь 10-3 К.
Слайд 20Сверхпроводимость
В 1957 г. Дж. Бардином, Л. Купером, Дж. Шрифером дано квантово-механическое объяснение
Сверхпроводимость
В 1957 г. Дж. Бардином, Л. Купером, Дж. Шрифером дано квантово-механическое объяснение

Электрон, движущийся среди положительно заряженных ионов, поляризует решетку (рис. 6.17), т.е. электростатическими силами притягивает к себе ближайшие ионы. Благодаря такому смещению ионов в окрестности траектории электрона локально возрастает плотность положительного заряда. Второй электрон, движущийся вслед за первым, будет притягиваться областью с избыточным положительным зарядом. В результате косвенным образом за счет взаимодействия с решеткой между электронами 1 и 2 возникают силы притяжения. Таким образом и получается связанная куперовская пара.
Слайд 21Сверхпроводимость
Поскольку силы притяжения невелики, спаренные электроны слабо локализованы в пространстве. Эффективный диаметр
Сверхпроводимость
Поскольку силы притяжения невелики, спаренные электроны слабо локализованы в пространстве. Эффективный диаметр

Чтобы уничтожить это состояние, необходимо разрушить куперовскую пару, т.е. затратить минимальную энергию (−2Δ) (на один электрон −Δ). В энергетическом спектре электронов образуется щель Еg = 2Δ,
определяющая уровень, на котором сконденсировались куперовские пары, от ближайшего разрешенного уровня, расположенного выше εf. Электроны сверхпроводника образуют единое целое квантовое состояние, которое в каждой точке пространства описывается амплитудой волновой функции и ее фазой.
 Стандарт cXML в корпоративных приложениях электронной коммерции
Стандарт cXML в корпоративных приложениях электронной коммерции Натюрморт в фотографии
Натюрморт в фотографии Золотой век русской культуры. Литература. Живопись
Золотой век русской культуры. Литература. Живопись титул констатирующего
титул констатирующего Повесть о настоящем человеке
Повесть о настоящем человеке Выпускающая кафедра«Механика механизмов и машин» Заведующий кафедрой Шевченко Игорь Владимирович
Выпускающая кафедра«Механика механизмов и машин» Заведующий кафедрой Шевченко Игорь Владимирович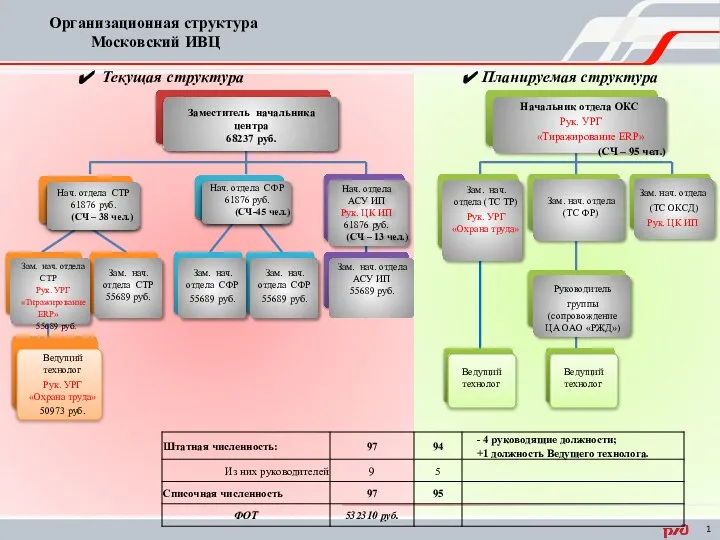 Организационная структура Московский ИВЦ
Организационная структура Московский ИВЦ День рождения Деда Мороза
День рождения Деда Мороза Поздравление с Новым годом
Поздравление с Новым годом Радиотехнические системы (РТС)
Радиотехнические системы (РТС) Презентация Microsoft PowerPoint [Автосохраненный]
Презентация Microsoft PowerPoint [Автосохраненный] Плюсы группы Т Плюс
Плюсы группы Т Плюс КВН – игра «В стране географов и географинь»
КВН – игра «В стране географов и географинь» Компьютерный кружок
Компьютерный кружок Изучение работы сварного соединения
Изучение работы сварного соединения  Осень… На улице холодно и сыро
Осень… На улице холодно и сыро Презентация на тему Познавательные способности
Презентация на тему Познавательные способности Башкирский государственный университет. Магистратура по социологии
Башкирский государственный университет. Магистратура по социологии Слово и время
Слово и время ИСПОЛЬЗОВАНИЕ МОБИЛЬНОГО КОМПЬЮТЕРНОГО КЛАССАВ УЧЕБНО-ВОСПИТАТЕЛЬНОМ ПРОЦЕССЕ МОУ СОШ 30
ИСПОЛЬЗОВАНИЕ МОБИЛЬНОГО КОМПЬЮТЕРНОГО КЛАССАВ УЧЕБНО-ВОСПИТАТЕЛЬНОМ ПРОЦЕССЕ МОУ СОШ 30 Презентация на тему Презентация "Буквы Уу Ээ"
Презентация на тему Презентация "Буквы Уу Ээ" Nature’s Sunshine Products
Nature’s Sunshine Products Православная молитва
Православная молитва ПСИХОЛОГИЧЕСКИЙ ВЕСТНИК
ПСИХОЛОГИЧЕСКИЙ ВЕСТНИК ИТОГИ РАБОТЫ ЗА 2011 ГОД
ИТОГИ РАБОТЫ ЗА 2011 ГОД Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании Северодвинск
Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании Северодвинск Орнамент
Орнамент Презентация на тему А нужен ли Калгон?
Презентация на тему А нужен ли Калгон?