Биомеханика. Термодинамика механохимических процессов

Термодинамика механохимических процессов
Живые организмы совершают механическую работу в изотермических (Т-const) и изобарических (P-const) условиях. Следовательно, они не тепловые машины.
Тепловая машина имеет нагреватель и холодильник. Чем больше разница температур
между нагревателем и холодильником, тем выше к.п.д.
Р
ΔV
Т1
Т2
1
2
3
4
К.п.д.= (Т1-Т2)/T1
Термодинамика механохимических процессов

Термодинамика механохимических процессов
При постоянной температуре тепловая энергия не может быть использована для совершения работы. Работа может совершаться за счет изменения конформации макромолекул. Последнее – энергозависимый процесс. Источником энергии является АТФ.
Таким образом, изменение свободной энергии (ΔG) – энергии, которую можно использовать для совершения работы – направленного перемещения под действием силы, равно изменению химического потенциала (Δμ) – энергии, которую необходимо затратить, чтобы синтезировать 1 моль вещества и перенести в данную точку.
ΔG=nΔμ (n-число молей).
Но чтобы ΔG могла быть использована для совершения работы, а не перешла в тепло, необходимо устройство, позволяющее совершить такое преобразование.

Термодинамика механохимических процессов
Механохимический процесс может выполняться циклически при переходе от одного химического потенциала к другому и возвращении к исходному. При этом во внешней среде совершается механическая работа. Пример - полимерное волокно, длина которого изменяется при изменении рН среды. Пусть это волокно растягивается силой F.
Работа такой системы равна A=FΔl, где Δl-удлинение волокна. При 100% к.п.д. будет выполняться равенство:
ʃFdl=- ʃ μdn. μ-химический потенциал, n-число молекул, испытывающих химические превращения.
К.п.д. системы, таким образом, равен ʃFdl/ ʃ μdn
A=- ΔG = (μ1-μ2) Δn - T ΔS
ʃ
ʃ
ʃ
ʃ

Термодинамика механохимических процессов
F
l
μ1
μ2
n1
n2
Механохимический цикл в координатах F и l
Термодинамика механохимических процессов

Структура мышцы и мышечных белков
Отдельное мышечное волокно имеет диаметр 20-80 мкм. Оно окружено мембраной, имеющей толщину 10 нм.
Волокно состоит из 1000-2000 более тонких волокон – миофибрилл, имеющих диаметр 1-2мкм.
Миофибриллы имеют оболочку, образованную трубочками и пузырьками саркоплазматического
ретикулюма. Сама фибрилла состоит из ряда белковых нитей – толстых и тонких. Они имеют гексагональную упаковку.

Структура миофибриллы
Z-линия
саркомер
А
Н
I
I
На продольном срезе миофибриллы видны т.н. Z-полоски. Пространство
между двумя соседними Z-полосками называется саркомером.
Центральная А-полоса анизотропна – обладает двойным лучепреломлением.
При растяжении покоящейся мышцы в центре А-полосы появляется Н-полоса
меньшей плотности. К Z-линиям примыкают изотропные I – полосы.

Структура миофибриллы
Z-линия
А
Н
I-полоса
Электронно-микроскопические исследования показали, что толстые нити (полоса А) образованы белком миозином, тонкие (I полосы) – белком актином. Каждая толстая нить состоит из 180-360 продольно ориентированных молекул миозина, ответственных за анизотропию плотной А-полосы.
Менее плотная I-полоса образована тонкими нитями белка актина, представляющего из себя двойную спираль (F-форма актина), возникшую в результате полимеризации глобулярного G-актина. На одну тонкую нить-до 800 глобул G-актина.
Тонкие нити F-актина проходят через Z-диски.

Структура актина
Тропонин
Тропонин
Тропомиозин
G актин
Актиновая нить представляет из себя двойную спираль
с субъединицами G-актина, повторяющимися через 5,46 нм вдоль нити. Расстояние между точками пересечения нитей - 36-37 нм. Диаметр двойной спирали актина: 6-8 нм.
В тонких нитях наряду с актином содержится тропомиозин – белок массой 70000 дальтон, имеющий длину 45 нм и соотношение длинной и короткой осей ок. 20.
Молекулы тропомиозина располагаются вдоль каждой борозды двойной спирали актина. Одна молекула контактирует с 7 молекулами G-актина.
Тропонин – глобулярный белок из трех компонент с с м.в. 37000, 23000 и 19000 дальтон. Глобула тропонина помещается вблизи каждой молекулы тропомиозина.

Структура миозина
ЛММ (150000)
ТММ
S2
(60000)
ТММ
S1
(120000)
Миозин представляет из себя фибриллярный белок. Он состоит
из молекул длиной 150 нм с диаметром 2 нм. Утолщенный
конец молекулы (головка) имеет длину 20 нм и ширину 4 нм. Молекула
построена из легкого меромиозина (ЛММ) и тяжелого меромиозина
(ТММ), имеющего два фрагмента S1 и S2. Правая часть молекулы
является двойной спиралью. Головка образована сегментом S1.
Общая молекулярная масса миозина: 500000 дальтон.

Структура миозина
При образовании толстой нити молекулы миозона агрегируют,
предположительно, в результате взаимодействий между “хвостами.”
Толстые нити миозина имеют диаметр 14 нм (тонкие актиновые-6-8нм).
Головки выступают из толстой нити. На одном уровне две выступающие
головки находятся друг против друга. Следующая пара расположена на
расстоянии 14,3 нм и повернута относительно первой на 122 градуса.
Структура как целое повторяется с периодом 42,9 нм.

Z-линия
саркомер
А
Н
I
I
Согласно данным световой и электронной микроскопии, при сокращении
мышцы происходит сужение I-полос без изменения протяженности А - полосы
Основные структурные особенности мышечного сокращения.

Z-линия
А
Н
I-полоса
Основные структурные особенности мышечного сокращения.
Согласно данным световой и электронной микроскопии, при сокращении
мышцы происходит сужение I-полос без изменения протяженности А – полосы
Z-диски движутся навстречу друг другу. I полосы исчезают вовсе.
Объем саркомера при этом , практически, не меняется, поскольку саркомер
становится толще.
Предполагается, что взаимодействие толстых и тонких нитей происходит посредством головок
миозина. Последние образуют мостики, соединяющие нити. Толкающее или тянущее усилие,
развиваемое мостиком, может быть результатом конформационной перестройки.

Биохимия мышечного сокращения.
Миозин + АТФ ↔Миозин-АТФ ↔Миозин ↔Миозин +АДФ+Ф
АДФ
Ф
1.Установлено, что миозин способен катализировать гидролиз АТФ.
2.Доказано, что АТФ расщепляется именно при сокращении мышцы.
3. Расщепление АТФ миозином сильно зависит от рН среды. Также для него необходимо присутствие ионов кальция и магния.
4. Активация мышечного сокращения происходит при передаче на мышцу через синапс нервного импульса. Возможна также активация искусственным электрическим импульсом. Нервный импульс вызывает высвобождение кальция из саркоплазматического ретикулюма.
медиатор
ПД

Тропонин
Тропонин
Тропомиозин
G актин
Ca2+ регулирует сократительный процесс, воздействуя на
тропонин. При отсутствии кальция тропонин в комплексе с
тропомиозином препятствуют взаимодействию актина с миозиновыми мостиками. Кальций, поступивший из СПР в саркоплазму, связывается с тропонином (ион-дипольные взаимодействия) и прекращает его ингибирующее действие.
В релаксированной мышце концентрация ионов кальция:
10-7 – 10-8 М. При активации: 10-4 – 10-5 М.
Обратно в СПР кальций закачивается активно.
Биохимия мышечного сокращения.
ПД
СПР
Ca2+
Ca2+
тропонин

Механика мышечного сокращения. Основные закономерности.
Различают изометрическое сокращение: при фиксированной длине. l-const
и изотоническое: укорочение мышцы при постоянной нагрузке . Р-const.
Хилл в 1938г. провел ряд экспериментов, в которых были установлены основные закономерности
Развиваемой мышцей мощности в зависимости от нагрузки.
Эксперименты были выполнены на икроножной мышце лягушки. Сокращение стимулировалось
Электродами.
+
-
Жестко закреплен
подвижен

Изотоническое сокращение.
При изотоническом сокращении (с постоянным грузом) после стимуляции напряжение (F/S=E) начинает расти, достигая максимума через 170 мс. Далее оно падает, полностью исчезая более чем через 1 секунду.
E, н/м2
t,c
При изотоническом сокращении укорочение (∆l) убывает с ростом веса груза (Р). Причем максимум укорочения достигается тем быстрее, чем больше груз.
Р,н
∆l
Р0

Уравнение Хилла.
Экспериментально установленные закономерности Хилл сформулировал в следующем
уравнении:
(P+a)V=b(P0-P)
Где Р – вес груза, подвешенного к мышце, Р0-максимальный груз, поддерживаемый мышцей
без удлинения, то есть максимальная сила, развиваемая мышцей в изотоническом режиме. V-скорость изотонического укорочения. a и b – константы.
Таким образом,
V=b(P0-P)/(P+a).
При Р=0 V=bP0/a. При Р=Р0 мышца перестает укорачиваться: V=0.
При Р˃Р0 мышца удлиняется. Это удлинение уже не описывается уравнением Хилла.

Уравнение Хилла.
Уравнение Хилла справедливо в условиях укорочения, идущего с постоянной скоростью и при длине
мышцы близкой к физиологической, поскольку развиваемое мышцей усилие зависит от длины саркомера.
Р0, н
Длина саркомера, мкм
4,0
2,0
0
На рисунке представлена зависимость максимально развиваемого усилия Р0 от длины саркомера.
Максимальное усилие соответствует максимальному перекрыванию головок миозиновых нитей с
нитями актина. При большом растяжении саркомера, как и при большом сжатии, это не достигается.

Работа, производимая мышцей при изотоническом сокращении.
А=РVt, где А-работа, Р-вес груза, V-скорость сокращения, t-время.
Согласно уравнению Хилла, ((P+a)V=b(P0-P)), а V=b(P0-P)/(P+a).
Следовательно, А=Рbt (P0-P)/(P+a).
Таким образом, А=0 при Р=Р0 и Р=0. Р макс = √[а(Р0+а)] –а.
Так как для большинства мышц а примерно равна 0,25Р0, то максимальная
мощность достигается при Р, имеющем величину ок. 0,31Р0.

Z-линия
А
Н
I-полоса
Максимальное напряжение, зафиксированное в икроножной мышце лягушки, Е=30н/см2, что соответствует 3• 10-10 н на миофибриллу. Считая, что каждый единичный элемент содержит одну молекулу миозина и каждый цикл замыкания-размыкания мостика сопровождается гидролизом одной молекулы АТФ, энергия которой, предположительно, используется на 50%, получим характеристики единичного элемента: сила 3• 10-12 н, расстояние 10-8 м, энергия 6 • 10-20 ДЖ.
Работа, производимая мышцей при изотоническом сокращении.
миозин

Термодинамика мышечного сокращения.
∆Q= ∆U+A. Согласно первому закону термодинамики, теплота поглощенная (или выделенная) системой (∆Q) равна изменению внутренней энергии (∆U) и работе, совершенной системой (А).
При сокращении мышцы теплота выделяется. Ее выделение, как и совершение работы, осуществляется за счет внутренней энергии системы:
∆U= ∆Q+А.
Установлено, что если мышца может сокращаться, то тепло, выделяемое мышцей во время одиночного сокращения, превышает таковое, выделенное за тот же период мышцей при изометрическом сокращении (в режиме тетануса). И эта разность пропорциональна только величине (Δl), на которую сократилась мышца, вне зависимости от P.
Q=a Δl, где а – коэффициент, характерный для данной мышцы, имеющий размерность силы.
К.п.д. мышцы = А/ (∆Q+А) • 100%. К.п.д. достигает 45% у лягушки и 75% у черепахи.

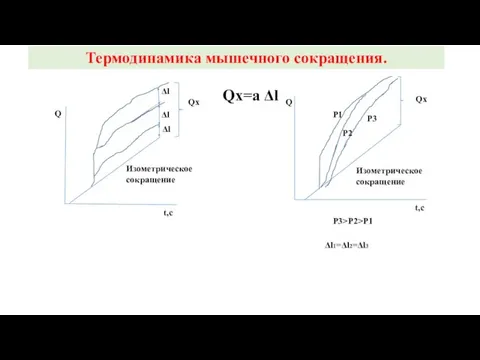
Термодинамика мышечного сокращения.
Qx=a Δl
t,c
Q
Qx
Δl
Δl
Δl
Изометрическое
сокращение
t,c
Q
Изометрическое
сокращение
Qx
Р1
Р2
Р3
Р3>P2>P1
Δl1=Δl2=Δl3

Теория мышечного сокращения.
Кинетическая теория Дщеревского, основные положения:
Три состояния поперечного мостика:
разомкнутое,
тянущее замкнутое (сила fэ),
замкнутое тормозящее. fэ постоянна и направлена к центру саркомера.
Переходы –процессы, не зависящие от состояния других мостиков
Константы к1, к и к2. Константы могут быть зависимы от скорости скольжения нитей. К2 и fэ от этого не зависят. Время жизни мостика в тянущем состоянии равен δ/u, где δ – путь, проходимый в этом состоянии, u – скорость движения.
К=u/δ

Скорость укорочения мышечного волокна (т.к. укорачиваются к центру)
V1=2Nu, где N-число саркомеров.
Сила F, генерируемая в половине саркомера,
F=nfэ-mfэ, где n и m – числа мостиков, находящихся, соответственно, в тянущем и тормозном состоянии.
Таким образом, по 2-му закону Ньютона
(n-m)f=2MNdu/dt + P1, М-масса груза.
du/dt=((n-m)f-P)/2MN
dn/dt=k1γ-kn, где γ– число мостиков в разомкнутом состоянии.
Введя α=γ+n+m, имеем
Dn/dt=k1(α-m-n)-(u/δ)n
Также:
Dm/dt= (u/δ)n – k2m
Если рассматривать состояние, когда число мостиков в каждом состоянии не меняется, и dn,m, γ/dt=0, имеем:
k1(α-m-n)-(u/δ)n=(u/δ)n – k2m=n-m-P/f =0
Отсюда получаем:
(P+(k1αf/k1+k2))u = (k1k2δ/(k1+k2))(αf-P)
Оно идентично уравнению Хилла:
(P+a)v=в(Ро-Р)
Теория мышечного сокращения.