популяции; эквивалент понятий «функция цели» и «критерий оптимальности», используемых при решении задач оптимизации.
Приспособленность особи – численное значение функции приспособленности, полученное для конкретной особи популяции.
Средняя приспособленность популяции – характеристика популяции, представляющая собой среднее арифметическое значение приспособленностей всех особей популяции на текущей эпохе эволюции.
Приспособленность лучшей особи – характеристика популяции, численно равная приспособленности лучшей особи текущей эпохи эволюции.
Решение – множество значений переменных лучшей особи, существовавшей когда-либо на протяжении всего эволюционного процесса.
Основные определения








 Жизненный цикл клетки
Жизненный цикл клетки Как вырастить дуб из желудя
Как вырастить дуб из желудя Царства живой природы
Царства живой природы Презентация на тему Физиологические адаптации (9 класс)
Презентация на тему Физиологические адаптации (9 класс)  Ах, картошка, объеденье
Ах, картошка, объеденье Биосфера Земли. Состав биосферы
Биосфера Земли. Состав биосферы Отряд Кошачьих
Отряд Кошачьих Рыбы пресного водоема
Рыбы пресного водоема Типы плодов
Типы плодов Стебель, его строение и значение
Стебель, его строение и значение Эмбриональное развитие человека
Эмбриональное развитие человека Биоформы в художественном конструировании
Биоформы в художественном конструировании 11.4 Закономерности наследования признаков. Моногибридное скрещивание
11.4 Закономерности наследования признаков. Моногибридное скрещивание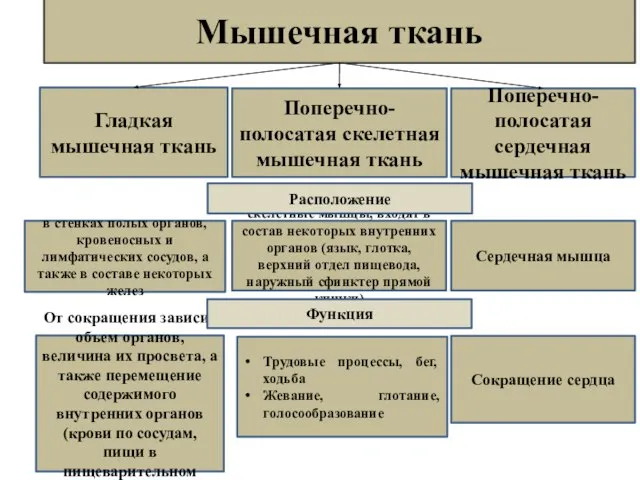 Мышечная ткань
Мышечная ткань Животные жарких стран
Животные жарких стран Роль железа в организме человека
Роль железа в организме человека Хемосинтез. Типы питания организмов
Хемосинтез. Типы питания организмов История систематики растении
История систематики растении Эмбриология_человека
Эмбриология_человека Никитский ботанический сад
Никитский ботанический сад Многообразие живого мира
Многообразие живого мира § 47. Автономный (вегетативный) отдел нервной системы 8 класс биология
§ 47. Автономный (вегетативный) отдел нервной системы 8 класс биология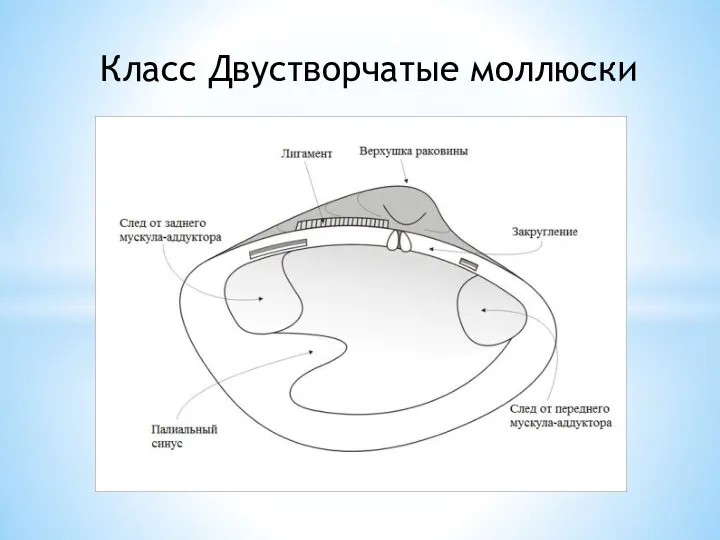 Класс Двустворчатые моллюски
Класс Двустворчатые моллюски The cell (from Latin cella, meaning small room)
The cell (from Latin cella, meaning small room) Корень. Корневые системы. 6 класс
Корень. Корневые системы. 6 класс Растениеводство. Смоленский лён
Растениеводство. Смоленский лён Строение тканей организма человека. Практическая работа № 2
Строение тканей организма человека. Практическая работа № 2 Китообразные животные
Китообразные животные