Модель изменения численности с учётом внутривидовой конкуренции (модель Ферхюльста)

Логистическая модель изменения численности популяции. Модель динамики численности популяции при ограниченных ресурсах предложил в 1838–1845 гг. французский математик П.Ф. Ферхюльст. Построение этой математической модели основано на следующих допущениях:
1 рост популяции ограничен количеством пищевых ресурсов и доступным пространством, пригодным для местообитания – т. е. биологической ёмкостью среды;
2 Скорости процессов размножения, естественной гибели и гибели в результате конкурентных конфликтов пропорциональны численности осо­бей в данный момент времени.
3 Физиологические и биохимические процессы не учитываются.
4 Учитывается внутривидовая конкуренция за место обитания, за пищевые ресурсы, которая тем интенсивнее, чем выше плотность популяции.
5 Популяция не взаимодействует с другими популяциями.

Введём обозначения:
N( t) – численность популяции в момент t;
Nmin – минимальная численность, обеспечивающая воспроизводство.
Будем считать, что средняя удельная рождаемость выражается положительной постоянной b, не зависящей от времени и размера популяции, а средняя удельная смертность в результате естественных причин выражается коэффициентом d, так же не зависящим от времени и плотности популяции.

По мере увеличения плотности популяции возрастает число конкурентных конфликтов со смертельным исходом, вероятность которых определяется величиной –d N2, где d – коэффициент гибели за счёт конкурентных конфликтов.
Составим уравнение динамики численности популяции:
; (2.1)
где r – биотический потенциал популяции (r = b–d).
Решаем нелинейное дифференциальное уравнение (2.1):
. (2.2)
(2.2)

Отсюда следует уравнение изменения численности в интегральной форме:
, при
. (2.3)

Поскольку численность популяции в естественных условиях никогда не остаётся постоянной, а испытывает колебания вблизи максимального значения, характеристической величиной процесса принято считать T0,9 – момент времени, когда численность популяции составляет 90 % от стационарной (максимальной). Координаты точки перегиба графика
N(t)–Tk и Nk (2.4) – это критический момент развития, когда начинает проявляться межвидовая конкуренция:
(2.4)

Если известно наибольшее число особей при данной биологической ёмкости среды (Nmax), уравнение для построения модели приобретает вид:
(2.5)

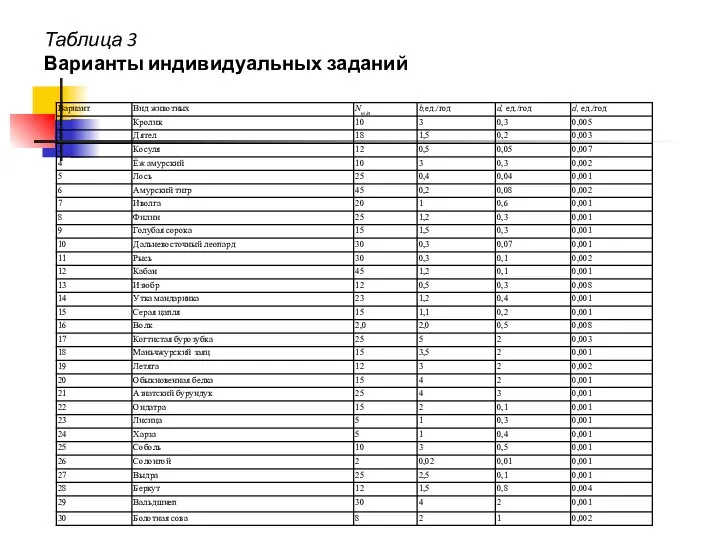
Задание.
1. Используя данные своего варианта (см. табл. 3) построить логистическую модель изменения численности популяции.
2. Интерпретировать модель, описав динамику популяции по следую­щим параметрам:
· Nmax – численность популяции в стационарном состоянии;
· Т0,9 – характеристическое время, когда численность популяции достигает 90 % от N(max);
· Nкрит и Ткрит – критическая численность и время, когда в популяции начинает проявляться внутривидовая конкуренция.
3. Сделать прогноз развития популяции.

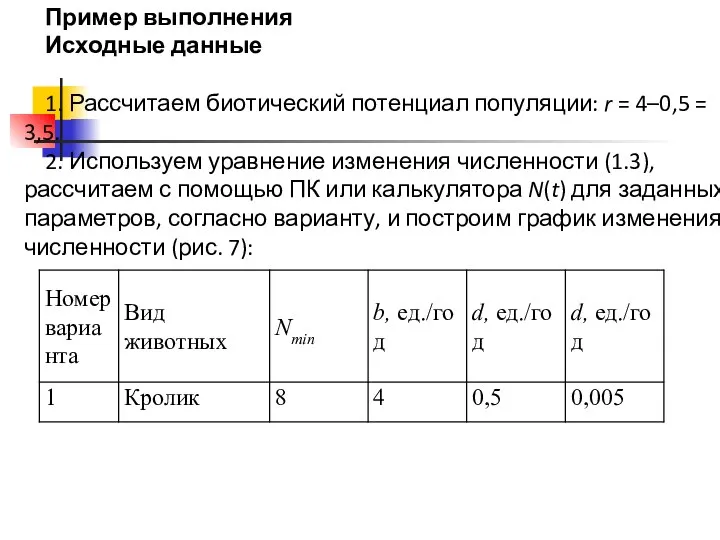
Пример выполнения
Исходные данные
1. Рассчитаем биотический потенциал популяции: r = 4–0,5 = 3,5.
2. Используем уравнение изменения численности (1.3), рассчитаем с помощью ПК или калькулятора N(t) для заданных параметров, согласно варианту, и построим график изменения численности (рис. 7):

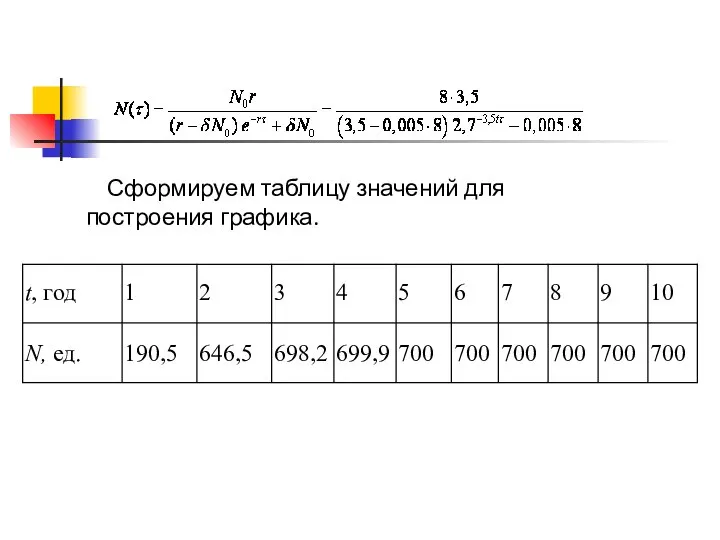
Сформируем таблицу значений для построения графика.

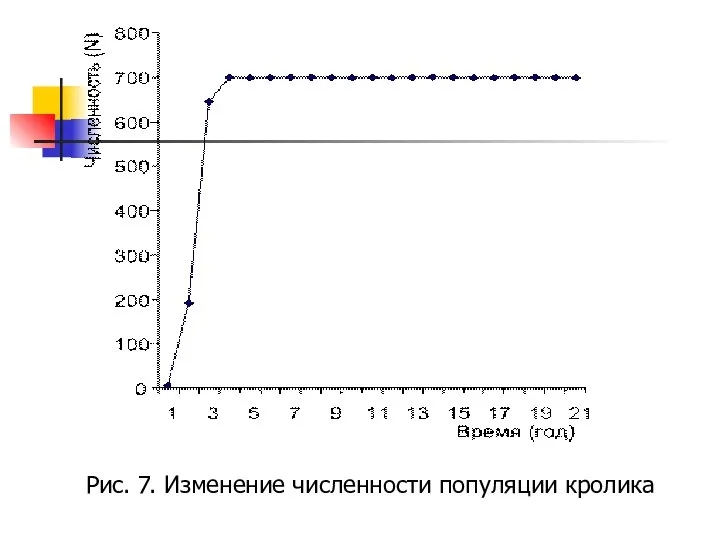
Рис. 7. Изменение численности популяции кролика

4. Оценим характеристические величины процесса по (2.3), (2.4):
Вывод: популяция кроликов обладает положительным биотическим потенциалом и способна увеличить свою численность в данных условиях до 700 особей за 4,5 года. Первые 3 года популяция находится в состоянии активного (экспоненциального) роста и по достижении численности в 350 особей основным фактором регуляции численности будет являться внутривидовая конкуренция за пищевые и пространственные ресурсы.

Таблица 3
Варианты индивидуальных заданий

Дополнительное задание
1. Пользуясь демографическими данными о росте численности населения (табл. 4), рассчитайте средний биотический потенциал популяции и постройте модель экспоненциального роста популяции Homo sapiens
(в мире в целом или по регионам).
2. Считая, что современная максимальная ёмкость биосферы по отношению к человеку составляет 6,5 млрд. чел, рассчитайте коэффициент смертности в результате внутривидовой конкуренции d и постройте модель логистического роста человеческой популяции.
3. В 2000 г. население земного шара составило около 6,2 млрд., а ёмкость среды ≈ 14 млрд. чел., определите год прекращения роста населения, исходя из того, что на Земле рождается 240 человек в минуту, а умирает 120.

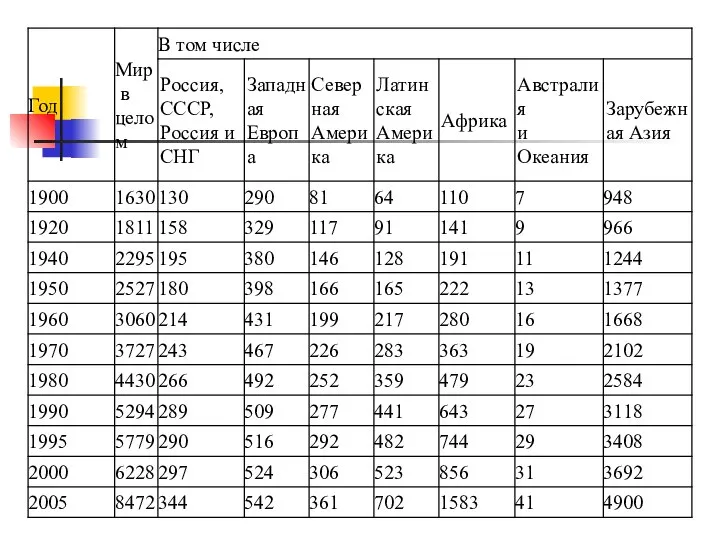
Таблица 4
Численность населения, млн. чел. в мире в ХХ в. и прогноз на ХХI в.
(по данным Интернет-проекта www. ecolife.ru)