Содержание
- 2. Предельные издержки. то Если если мало. Предельные издержки показывают дополнитель- ные затраты на производство дополнительной единицы
- 3. Предельный доход (предельная выручка). Пусть Q – объем произведенной продукции. R(Q) – доход от ее реализации.
- 4. то Если если мало. Предельный доход показывает дополнитель- ный доход от реализации дополнительной единицы продукции. Предельный
- 5. Предельный доход (предельная выручка). Пример 1. Производитель продает продукт на рынке совершенной конкуренции. Рыночная цена равна
- 6. Предельный доход (предельная выручка). Пример 2. Производитель продает продукт на монопольном рынке. функция спроса 1) Найти
- 7. Эластичность в экономике. Эластичность показывает на сколько процентов изменится функция при изменении аргумента на 1%.
- 8. Эластичность в экономике. а) Пусть Q(P) – функция спроса от цены. - показывает на сколько процентов
- 9. 2. Эластичность в экономике. Пример 1 Q(P)=-0,05P+10 – функция спроса на некоторый продукт. 1) Найти эластичность
- 10. 2. Эластичность в экономике. Пример 2 Функция спроса задана формулой Q(p)= 2 / p 1) Какова
- 11. Эластичность в экономике. Если то спрос называют эластичным. Если то спрос называют неэластичным. Если то спрос
- 12. 2. Эластичность в экономике. б) Пусть Q(I) – функция спроса от дохода. - показывает на сколько
- 13. Эластичность в экономике. в) Пусть Q(P) – функция предложения от цены. - показывает на сколько процентов
- 14. Соотношение эластичности спроса и предельного дохода. Пусть Q(P) – функция спроса на некоторый товар; R(P)=P·Q(P) –
- 15. Соотношение эластичности спроса и предельного дохода. Если т.е. спрос эластичен, то т.е. увеличение цены приведет к
- 16. Соотношение эластичности спроса и предельного дохода. Если т.е. спрос неэластичен, то т.е. увеличение цены приведет к
- 17. Соотношение эластичности спроса и предельного дохода. Если т.е. спрос с единичной т.е. увеличение цены не изменит
- 18. Соотношение эластичности спроса и предельного дохода. Вывод: С возрастанием цены для продукции с эластичным спросом суммарный
- 19. Соотношение эластичности спроса и предельного дохода. Пример: Функция спроса на некоторый товар Q(P)=-2P+12 при P 6.
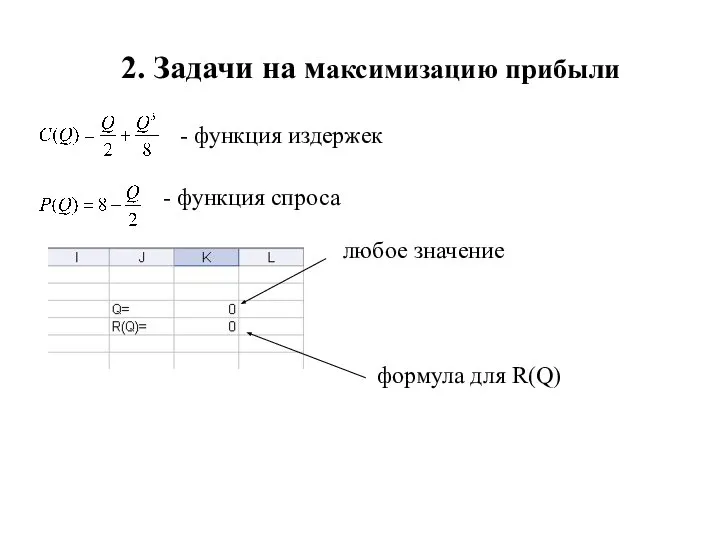
- 20. 2. Задачи на максимизацию прибыли - функция издержек - функция спроса Составить функцию прибыли П(Q) Найти
- 21. 2. Задачи на максимизацию прибыли - функция издержек - функция спроса любое значение формула для R(Q)
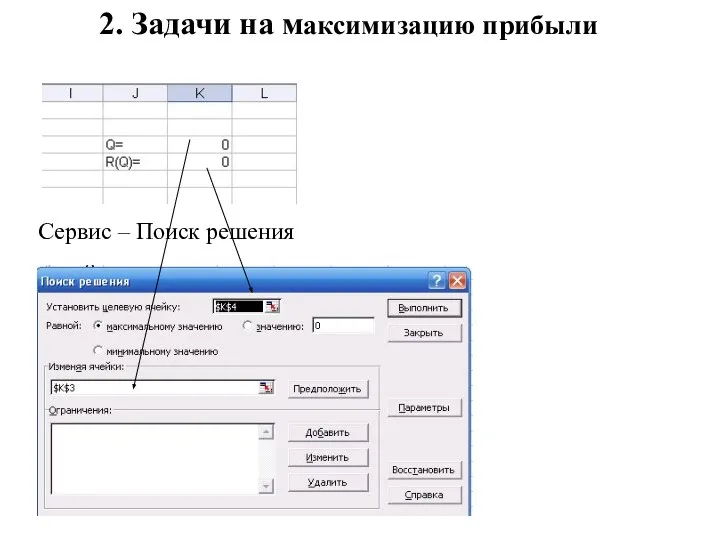
- 22. 2. Задачи на максимизацию прибыли Сервис – Поиск решения
- 23. 2. Задачи на максимизацию прибыли
- 24. 2. Задачи на максимизацию прибыли - функция издержек - функция спроса Составить функцию прибыли П(Q) Найти
- 25. 2. Задачи на максимизацию прибыли 4.181; 4.182; 4.184-4.186; 4.187-4.190; 4.193; 4.194
- 26. 3. Задачи на максимизацию прибыли функций двух и более переменных Пример 1 Фирма производит 2 товара
- 27. Необходимое условие экстремума. Пусть - точка экстремума функции z=f(x,y). Тогда
- 28. Если то - точка максимума Если то - точка минимума Если то не является точкой экстремума
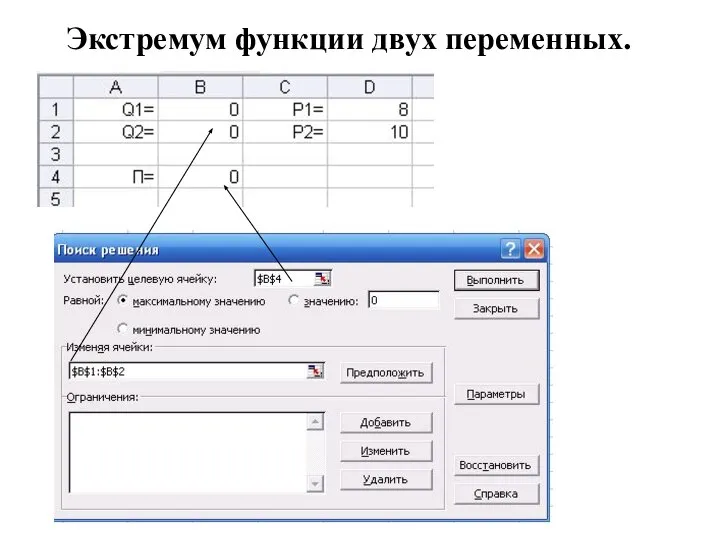
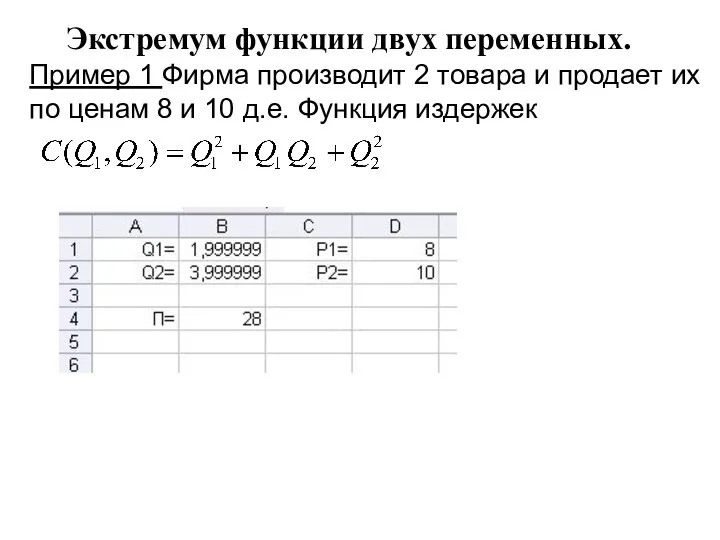
- 29. Экстремум функции двух переменных. Пример 1 Фирма производит 2 товара и продает их по ценам 8
- 30. Экстремум функции двух переменных.
- 31. Экстремум функции двух переменных. Пример 1 Фирма производит 2 товара и продает их по ценам 8
- 32. 3. Задачи на максимизацию прибыли функций двух и более переменных 5.229-5.232
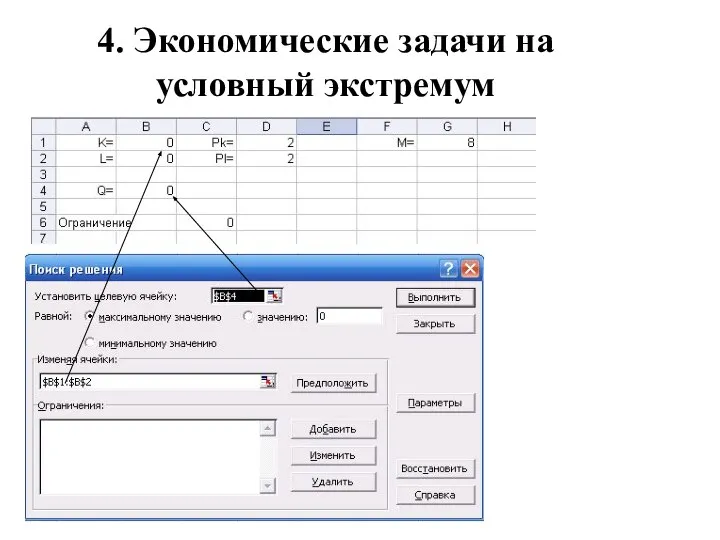
- 33. 4. Экономические задачи на условный экстремум Пример. Q(K,L)=KL – производственная функция. Единица капитала стоит 2 д.е.,
- 34. 4. Экономические задачи на условный экстремум Пример. Q(K,L)=KL – производственная функция. Единица капитала стоит 2 д.е.,
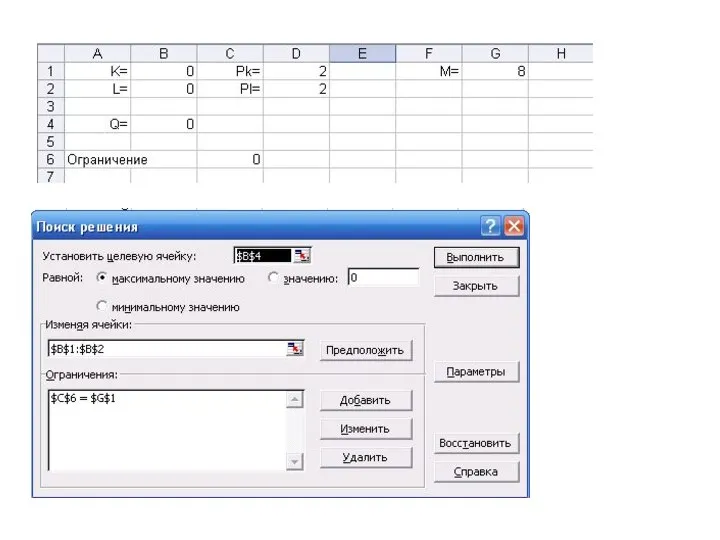
- 35. 4. Экономические задачи на условный экстремум
- 36. 4. Экономические задачи на условный экстремум
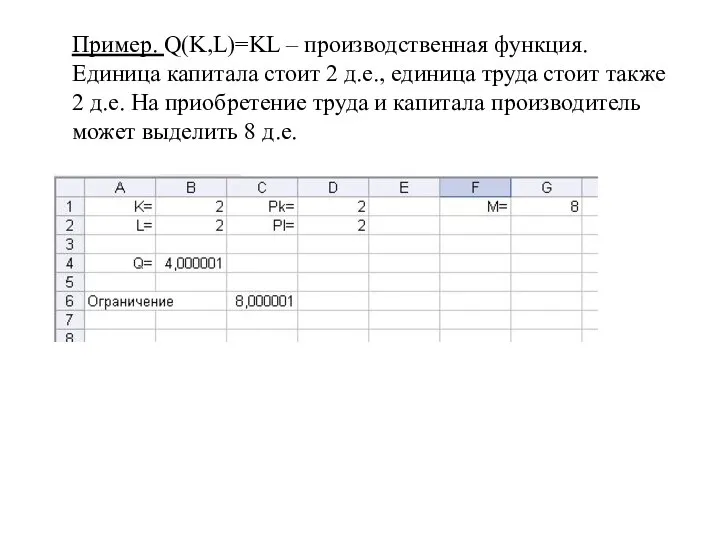
- 38. Пример. Q(K,L)=KL – производственная функция. Единица капитала стоит 2 д.е., единица труда стоит также 2 д.е.
- 40. Скачать презентацию






























 Экономическое развитие. Экономический цикл
Экономическое развитие. Экономический цикл Фондовая биржа
Фондовая биржа Обрабатывающая промышленность как драйвер экономического роста
Обрабатывающая промышленность как драйвер экономического роста Методология экономической диагностики деятельности организации
Методология экономической диагностики деятельности организации zBicZNAQDI7Uf7PmsnrnJw
zBicZNAQDI7Uf7PmsnrnJw Постоянные и переменные издержки
Постоянные и переменные издержки Экономика потребителя
Экономика потребителя Организация Восточно - карибских государств
Организация Восточно - карибских государств Валютное регулирование и валютный контроль
Валютное регулирование и валютный контроль Экономико-правовой аспект увеличения розничной торговли фруктами, овощами и картофелем
Экономико-правовой аспект увеличения розничной торговли фруктами, овощами и картофелем Валютные условия внешнеэкономических сделок Подготовила : Назаренко А.И. Сударкина А.Г. Гр. МЭ-091
Валютные условия внешнеэкономических сделок Подготовила : Назаренко А.И. Сударкина А.Г. Гр. МЭ-091 Подбор и адаптация персонала
Подбор и адаптация персонала Китай
Китай Средства стимулирования сбыта: виды и особенности
Средства стимулирования сбыта: виды и особенности Основы формирования цены в рыночных условиях
Основы формирования цены в рыночных условиях Оборачиваемость. Рентабельность
Оборачиваемость. Рентабельность Современные технологии организации снабжения
Современные технологии организации снабжения Амортизация основных фондов
Амортизация основных фондов Безработица
Безработица Экономическая безопасность предприятия: оценка состояния и направления обеспечения
Экономическая безопасность предприятия: оценка состояния и направления обеспечения Расчет производственного цикла
Расчет производственного цикла Решение задач - основы
Решение задач - основы Производители ПВХ в РФ
Производители ПВХ в РФ Богатые и бедные 7 кл
Богатые и бедные 7 кл Экономические основы деятельности фирмы
Экономические основы деятельности фирмы Государственное регулирование
Государственное регулирование Оценка регионов РК по группе показателей, характеризующих их ёмкость
Оценка регионов РК по группе показателей, характеризующих их ёмкость Nordship - закажи и получи сейчас
Nordship - закажи и получи сейчас