Содержание
- 2. Produkcja oznacza: Dostosowywanie i przekształcanie dóbr przyrody w produkty użyteczne dla człowieka – zaspakajające jego potrzeby
- 3. Funkcja produkcji Podstawowa kategoria teorii produkcji Q = (A, B, C...N) Q – ilość A, B,
- 4. Uproszczony zapis Q = f (K, L) L – nakłady pracy K – nakłady kapitału Zmiany
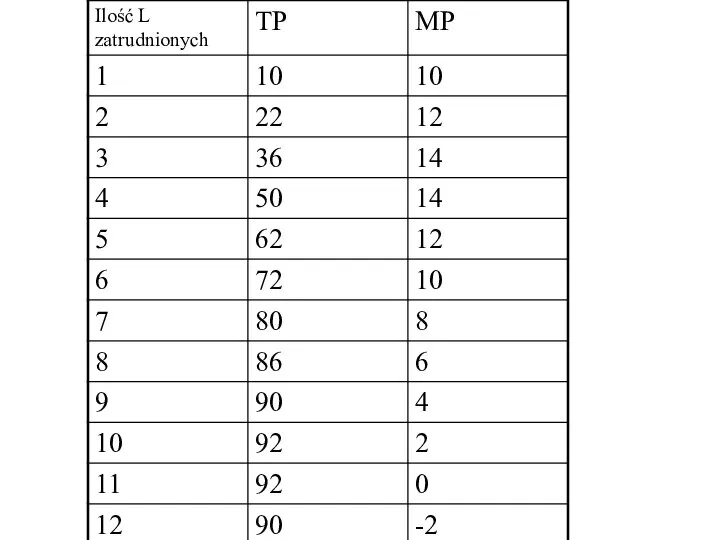
- 5. Produkcję można mierzyć Produkt całkowitym TP – wielkość produkcji przy danym kapitale, którą dają kolejne jednostki
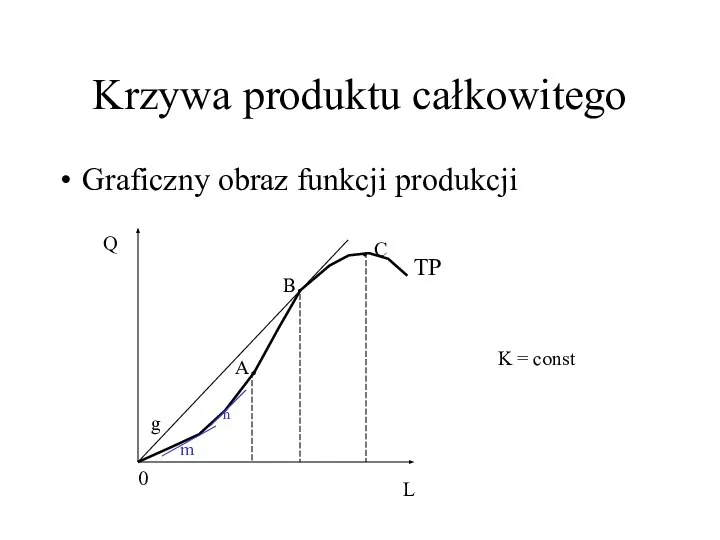
- 6. Krzywa produktu całkowitego Graficzny obraz funkcji produkcji 0 L Q TP B. g A. . C
- 7. Produkcję można mierzyć Produktem przeciętnym AP AP = TP/ L ilość produktu całkowitego na 1 jednostkę
- 8. Produkcję można mierzyć Produktem krańcowym MP MP = ΔTP Δ L MP jest zmianą wielkości produktu
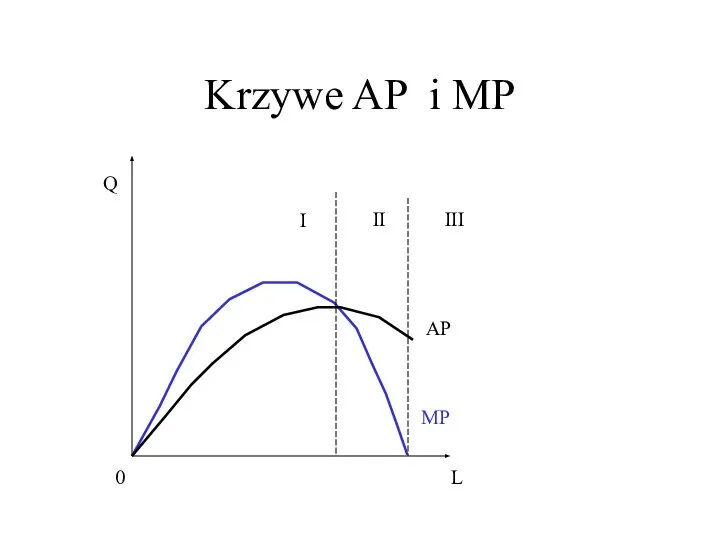
- 9. Krzywe AP i MP 0 Q L MP AP I II III
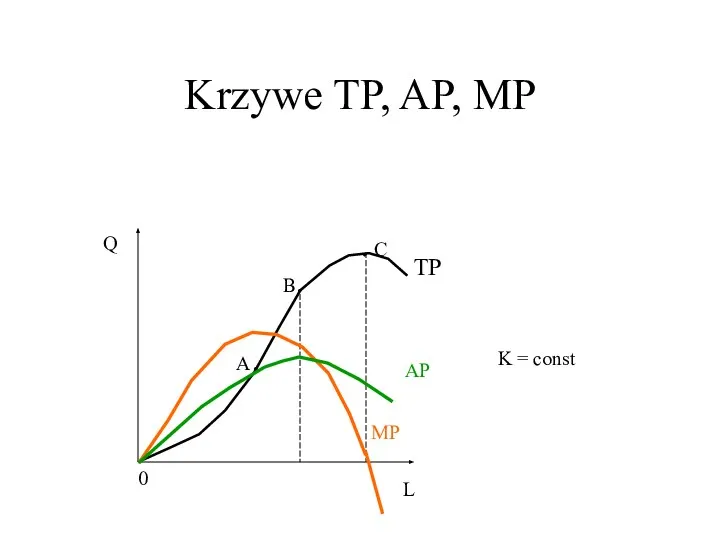
- 10. Krzywe TP, AP, MP 0 L Q TP B. A. . C K = const MP
- 11. Prawo malejących przychodów krańcowych Utrzymując technologie i wszystkie nakłady, z wyjątkiem jednego, na stałym poziomie, gdy
- 13. Czy działa prawo malejących przychodów ? Jego autorem jest Robert Malthus, w swojej teorii ludnościowej( Prawo
- 14. W długim okresie wszystkie czynniki produkcji są zmienne Nie działa więc prawo malejących przychodów krańcowych Zmieniają
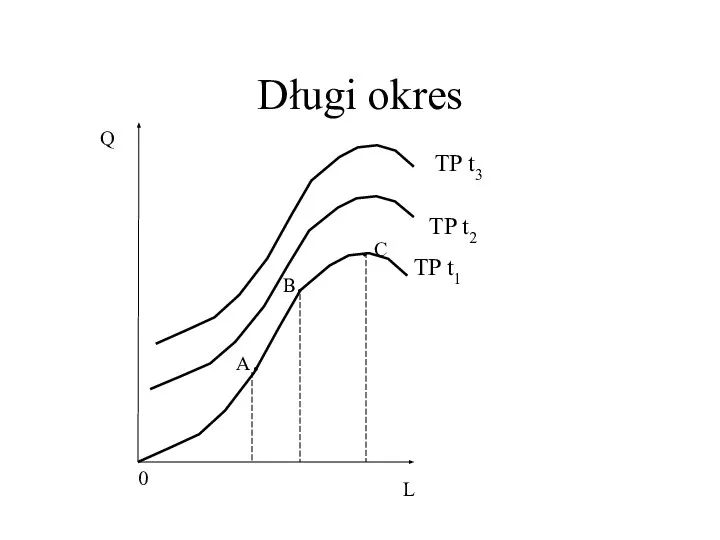
- 15. Długi okres 0 L Q TP t1 B. A. . C TP t2 TP t3
- 16. Kiedy działa prawo malejących przychodów W specyficznie określonych warunkach: przynajmniej jeden czynnik jest stały (K) Nie
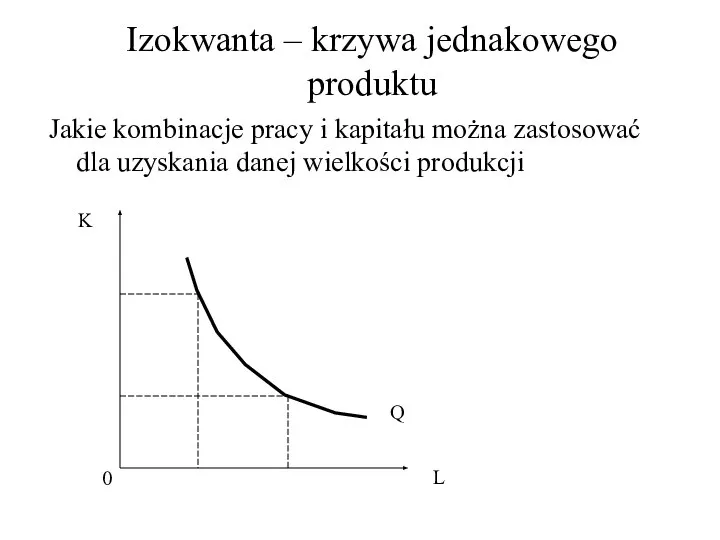
- 17. Izokwanta – krzywa jednakowego produktu Jakie kombinacje pracy i kapitału można zastosować dla uzyskania danej wielkości
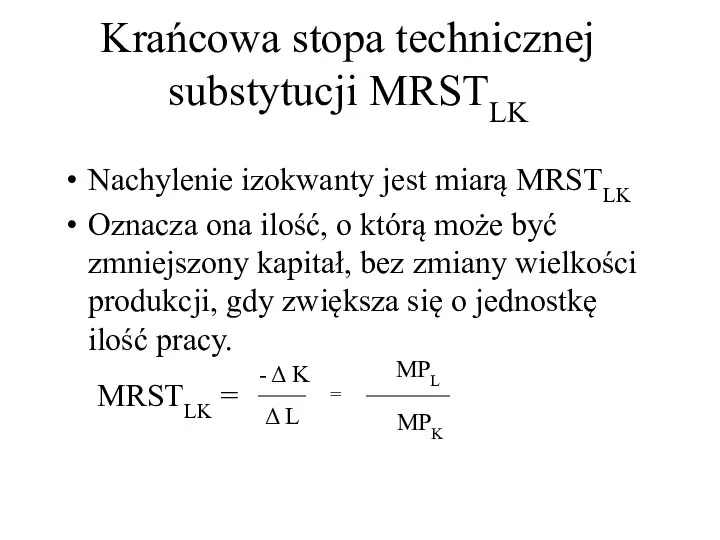
- 18. Krańcowa stopa technicznej substytucji MRSTLK Nachylenie izokwanty jest miarą MRSTLK Oznacza ona ilość, o którą może
- 19. Mapa izokwant Zakładając, że ilości czynników produkcji mogą być zmienione można wykreślić mapę izokwant 0 K
- 20. Podsumowując Funkcja produkcji opisuje, jak zmienia się wielkość produkcji w miarę zwiększania ilości zmiennego czynnika produkcji.
- 21. Koszty produkcji (wartościowe ujęcie produkcji) Użycie zasobów na dany efekt gospodarczy kosztuje (nakłady mnożymy przez cenę
- 22. Koszty okazji Kosztem użycia zasobów w dany sposób jest wartość tego, co te zasoby mogłyby wytworzyć,
- 23. Przykład kosztów okazji Koszty okazji zastosowania nakładów pracy Mamy małą firmę, której właściciel sam pracuje. Firma
- 24. Koszt księgowy a koszt ekonomiczny 100.000 – 60.000(koszty księgowe) = 40.000 zysk księgowy 100.000 – 60.000
- 25. Koszt okazji zastosowania kapitału Mając 200.000 PLN właściciel podejmuje się produkcji określonych dóbr (np. kostki brukowej).
- 26. Amortyzacja - przykład Firma „OK. spółka z o.o.” produkująca okna i drzwi kupuje samochód dostawczy za
- 27. Amortyzacja – przykład cd. NIE Zakup samochodu to powiększenie majątku trwałego firmy (czyli inwestycja), 60.000 PLN
- 28. Amortyzacja- przykład cd. Księgowi zakładają, że zakupiony samochód będą zaliczać w koszty następująco: 60.000PLN/ 5 lat
- 29. Plan amortyzacji - przykład Pierwsza kwota (rata) amortyzacji zostanie zaliczona w koszty dopiero w grudniu 2006
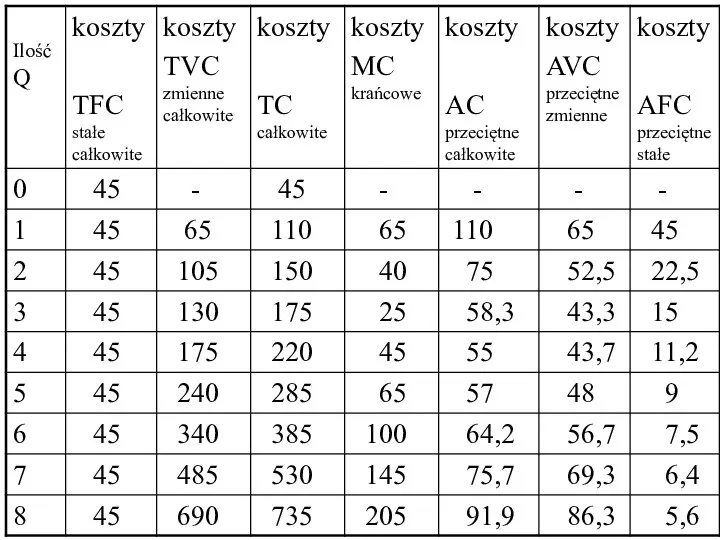
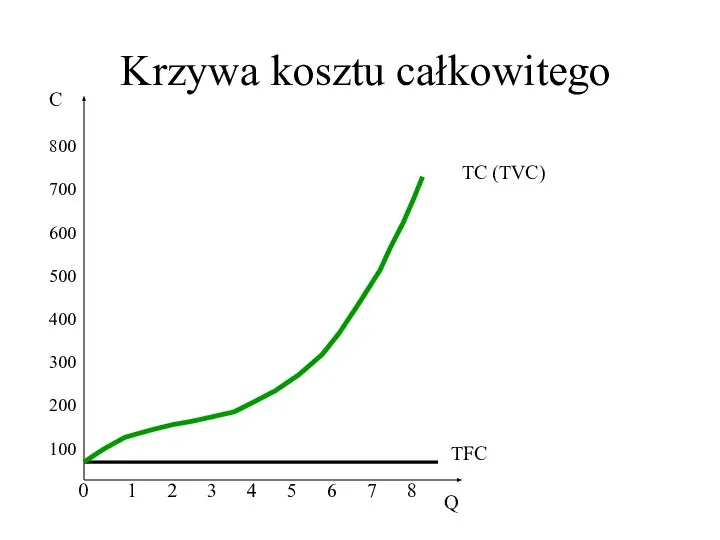
- 31. Krzywa kosztu całkowitego 0 C Q 800 700 600 500 400 300 200 100 1 2
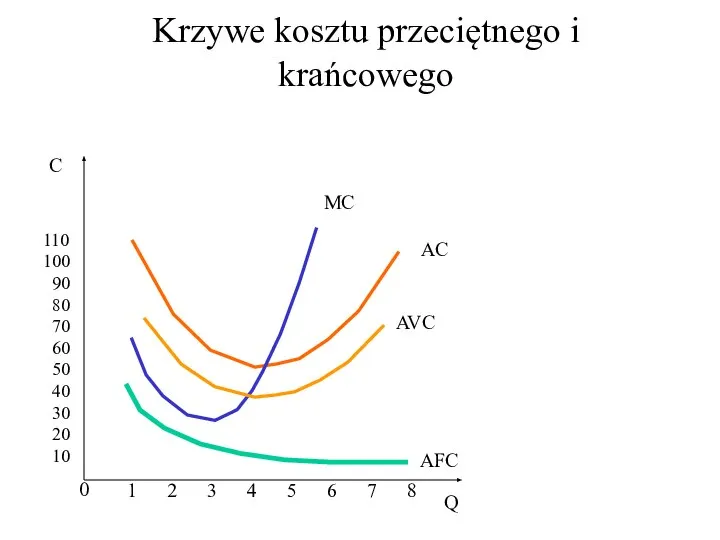
- 32. Krzywe kosztu przeciętnego i krańcowego 0 C Q 110 100 90 80 70 60 50 40
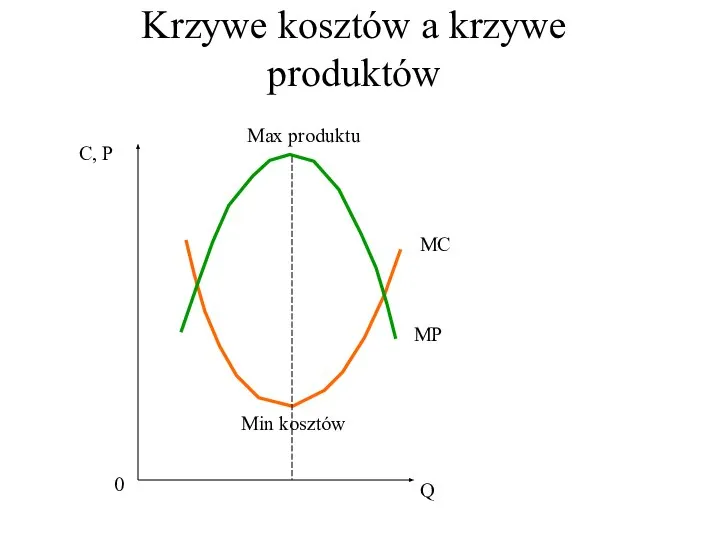
- 33. Krzywe kosztów a krzywe produktów Q 0 C, P MC MP Min kosztów Max produktu
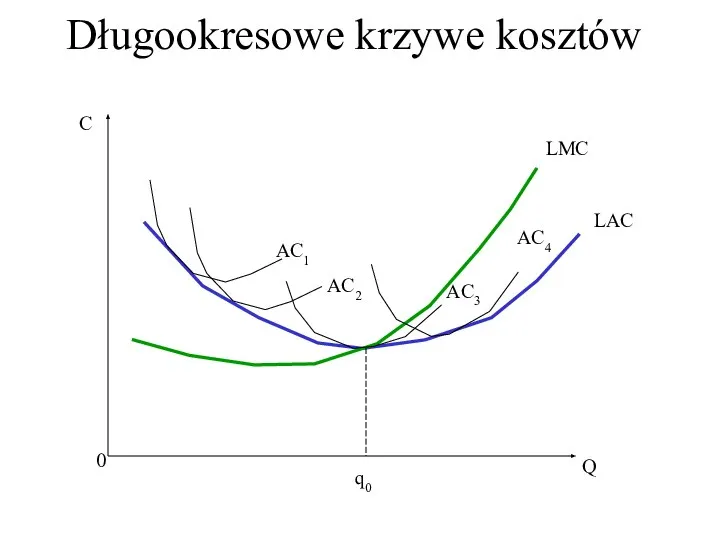
- 34. Długookresowe krzywe kosztów C Q 0 LAC LMC AC1 AC3 AC2 AC4 q0
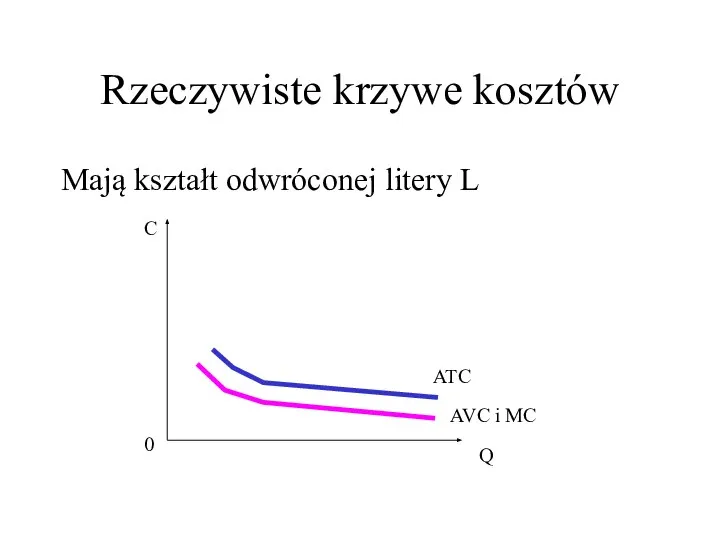
- 35. Rzeczywiste krzywe kosztów Mają kształt odwróconej litery L C Q 0 ATC AVC i MC
- 36. Zasada najniższego kosztu Krańcowy produkt L = Krańcowy produkt K Cena L Cena K Krańcowy wkład
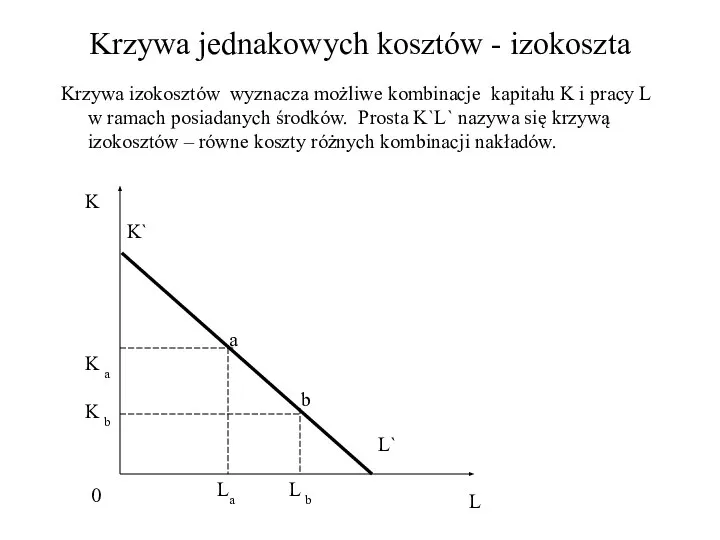
- 37. Krzywa jednakowych kosztów - izokoszta Krzywa izokosztów wyznacza możliwe kombinacje kapitału K i pracy L w
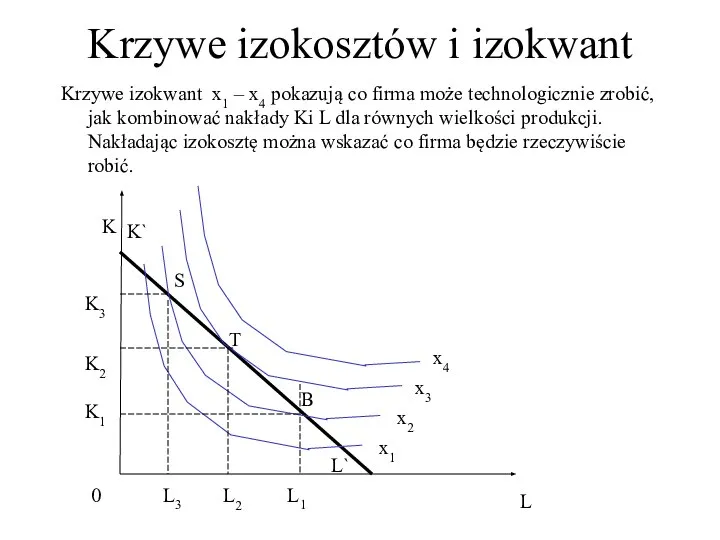
- 38. Krzywe izokosztów i izokwant Krzywe izokwant x1 – x4 pokazują co firma może technologicznie zrobić, jak
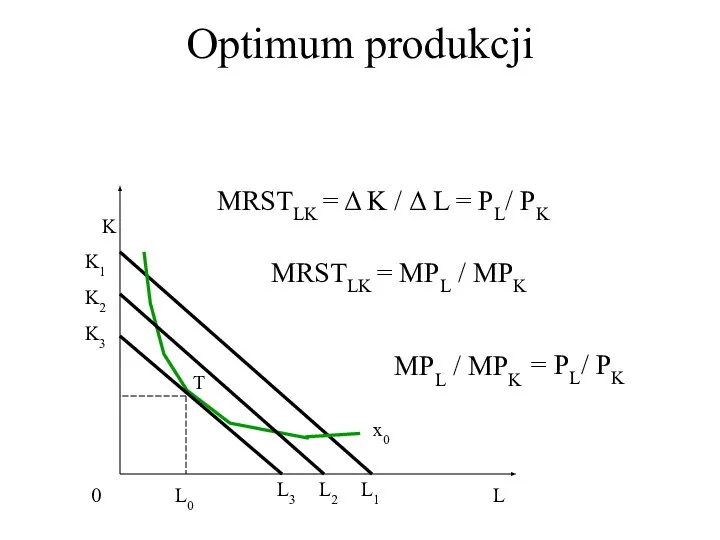
- 39. Optimum produkcji 0 K L x0 K3 K2 K1 L0 L3 L2 T L1 MRSTLK =
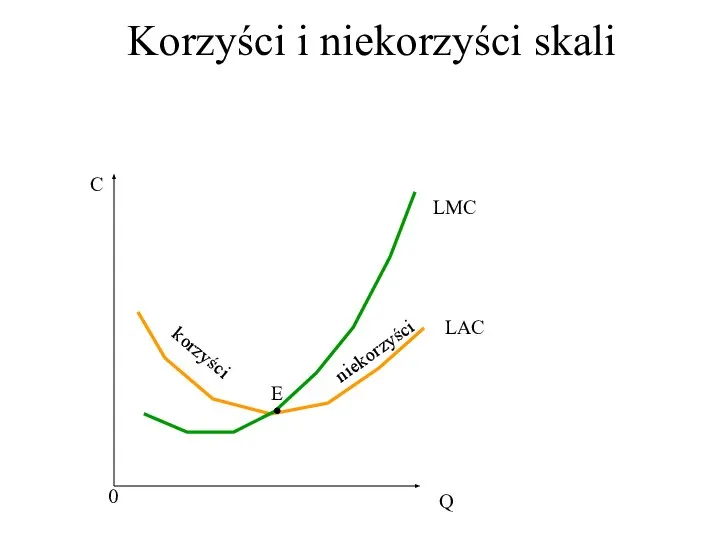
- 40. Korzyści i niekorzyści skali 0 C Q LMC LAC . E korzyści niekorzyści
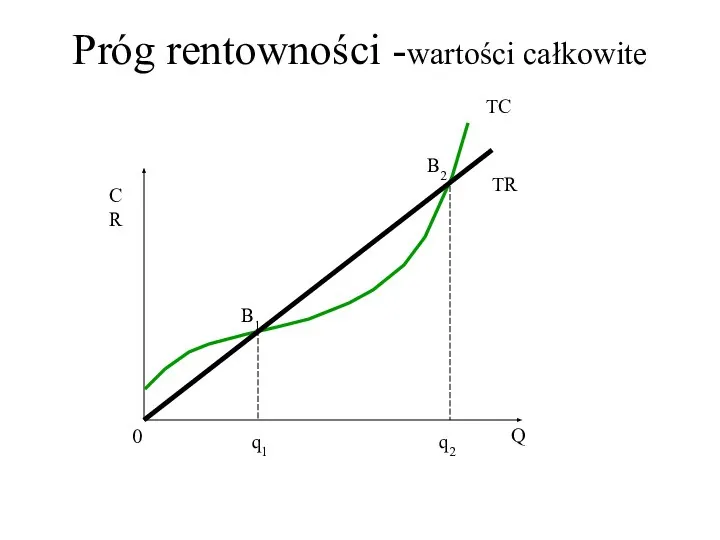
- 41. Próg rentowności -wartości całkowite C R Q 0 TC TR q1 q2 B1 B2
- 42. Próg rentowności – praktyczne zastosowanie analizy kosztów Przy sprzedaży mniejszej niż q1 firma nie pokrywa kosztów
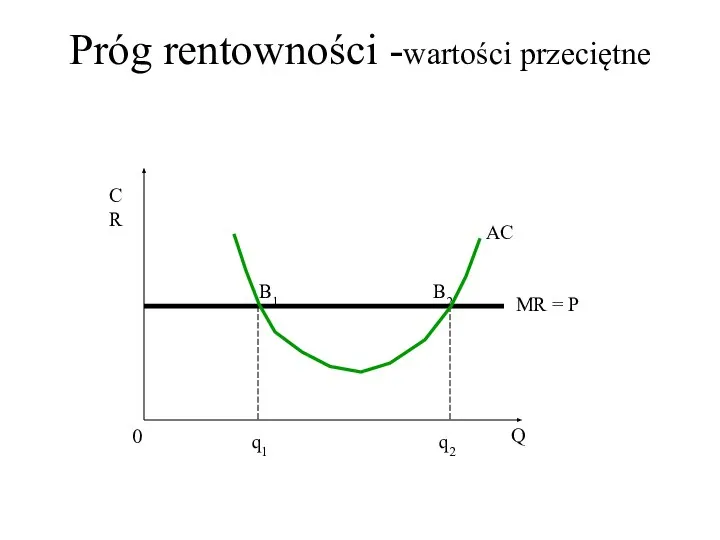
- 43. Próg rentowności -wartości przeciętne C R Q 0 q1 q2 B2 MR = P AC B1
- 45. Скачать презентацию























 Постановление Правительства РФ от 3 декабря 2020 года. О минимальной доле закупок товаров российского происхождения
Постановление Правительства РФ от 3 декабря 2020 года. О минимальной доле закупок товаров российского происхождения Глобальные риски 2020 года
Глобальные риски 2020 года Место и роль государства в экономике. Практика 1
Место и роль государства в экономике. Практика 1 Кількісний аналіз економіки бізнес –структури. Аналіз міжнародного бізнесу
Кількісний аналіз економіки бізнес –структури. Аналіз міжнародного бізнесу Экономическое значение кредита. Функции кредита Подготовила: Клеутина С.А. Группа МЭ-092
Экономическое значение кредита. Функции кредита Подготовила: Клеутина С.А. Группа МЭ-092 Экономический кризис
Экономический кризис Высшее образование в области государственного и муниципального управления. Лекция 1
Высшее образование в области государственного и муниципального управления. Лекция 1 Сравнительный анализ вариантов развития Челябинского метрополитена
Сравнительный анализ вариантов развития Челябинского метрополитена Итоги работы промышленного комплекса Липецкой области за 2017 год и перспективы развития на 2018 год
Итоги работы промышленного комплекса Липецкой области за 2017 год и перспективы развития на 2018 год Экономика для человека. Стратегия опережающего развития
Экономика для человека. Стратегия опережающего развития Циклическая природа распространения инноваций
Циклическая природа распространения инноваций Устойчивость работы объектов экономики в чрезвычайных ситуациях
Устойчивость работы объектов экономики в чрезвычайных ситуациях Развитие Красноярского Края в ближайшие 50 лет
Развитие Красноярского Края в ближайшие 50 лет Спрос и предложение. Дополнительные аспекты
Спрос и предложение. Дополнительные аспекты Уильям Спенсер Викри
Уильям Спенсер Викри Экономический рост России и ее интеллектуальный потенциал
Экономический рост России и ее интеллектуальный потенциал Фирма в экономической теории. Цели фирмы
Фирма в экономической теории. Цели фирмы Управление кластерным взаимодействием в СПО
Управление кластерным взаимодействием в СПО Занятость и безработица
Занятость и безработица Какие бывают потребности. 6 класс
Какие бывают потребности. 6 класс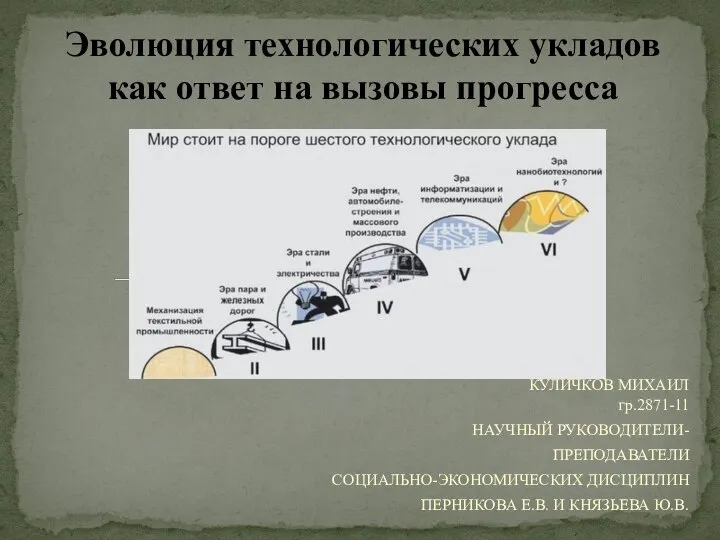 Эволюция технологических укладов как ответ на вызовы прогресса
Эволюция технологических укладов как ответ на вызовы прогресса РФ на современном этапе
РФ на современном этапе Управление структурой капитала
Управление структурой капитала Экономика и экология
Экономика и экология Матричные методы оценки конкурентоспособности
Матричные методы оценки конкурентоспособности Вторичный рынок ценных бумаг
Вторичный рынок ценных бумаг Стратегия и тактика конкурентной борьбы на рынке ресторанных услуг города Санкт-Петербург
Стратегия и тактика конкурентной борьбы на рынке ресторанных услуг города Санкт-Петербург Институциональная экономика. Вступление
Институциональная экономика. Вступление