Содержание
- 2. Постановка проблемы кооперативного принятия решений Примеры: Финансирование общественных благ Трагедия общины (истощение ресурсов из-за чрезмерного использования)
- 3. Системы голосования Системы голосования: Мажоритарная (Россия, президентские выборы – два тура) Пропорциональная (Россия, парламентские выборы, с
- 4. Правило Кондорсе vs Борда Правило относительного большинства: 3 5 7 6 A A B C A
- 5. Парадокс Кондорсе Победитель по Кондорсе может отсутствовать: К > П > Ч > K К Ч
- 6. Борда ≠ Кондорсе Пример для строго монотонного правила подсчета очков : 3 2 1 1 s2
- 7. Профиль Страффина 4 1 3 A C E E B D A A C B D
- 8. Аксиоматический подход Однозначность – правило всегда дает сделать однозначный выбор. Не вы-полняется для анонимных и нейтральных
- 9. Последовательные сравнения по правилу большинства 1. Не выполняется нейтральность. Повестка определяет контроль над выборами. Побед. A
- 10. Аксиоматический подход Монотонность – увеличившаяся поддержка кандидата не может уменьшить шанса быть избранным. Не выполняется для
- 11. Аксиоматический подход Пополнение – если 2 независимые группы избирателей выбирают кандида-та A, то, объединившись, они выберут
- 12. Аксиоматический подход Неманипулируемость (независимость от посторонних альтернатив) – нельзя увеличить свою полезность, ведя стратегическое голосование. При
- 13. Случай однопиковых предпочтений Коллективный выбор температуры в комнате (открыть / закрыть окно) Из двух альтернатив побеждает
- 14. ЦСКА, Локомотив, Спартак Л Л С Ц С Ц У Локомотива при игре с ЦСКА и
- 15. Выполнение аксиом для различных правил голосования О – относительное большинство Б – правило Борда A –
- 16. Теорема Эрроу N={1,2,…,n} – избиратели, A={a,b,c,…} – кандидаты. P(A) – множество линейных порядков на A R(A)
- 17. Метод Шульце (1997) (метод разъезженного пути) Избиратели указывают в бюллетене предпочтения относительно кандидатур. 1 – наиболее
- 18. Метод Шульце (1997). Пример 45 избирателей, 5 кандидатов: 5 5 8 3 7 2 7 8
- 19. Метод Шульце. Еще примеры Кондорсе: 23 17 2 10 8 A B B C C B
- 21. Скачать презентацию
Слайд 2Постановка проблемы
кооперативного принятия решений
Примеры:
Финансирование общественных благ
Трагедия общины (истощение ресурсов из-за чрезмерного использования)
Дилемма
Постановка проблемы
кооперативного принятия решений
Примеры:
Финансирование общественных благ
Трагедия общины (истощение ресурсов из-за чрезмерного использования)
Дилемма

Асимметричность информации (отрицательный отбор; моральный риск)
Многие общественно значимые решения не могут приниматься на основе рыночных механизмов, поскольку кооперативные возможности не будут эффективно использованы при децентрализованных действиях агентов.
Индивидуальные предпочтения → коллективный выбор (принимают все!)
Предположение: пренебрегаем мнением меньшинства; из двух альтернатив
побеждает та, за которую проголосовало более 50% человек!
Практика: альтернатив более двух!
Правило большинства – единственный метод, удовлетворяющий требованиям
Анонимность (равноправие избирателей).
Нейтральность (равноправие кандидатов).
Монотонность (усиление поддержки не подвергает сомнению избрание).
Слайд 3Системы голосования
Системы голосования:
Мажоритарная (Россия, президентские выборы – два тура)
Пропорциональная (Россия, парламентские выборы,
Системы голосования
Системы голосования:
Мажоритарная (Россия, президентские выборы – два тура)
Пропорциональная (Россия, парламентские выборы,

Смешанная (Россия, парламентские выборы, до 2003 года)
Голосование выборщиков (США, президентские выборы)
Парадоксы «голосования выборщиков»:
Победитель может набрать меньше голосов
избирателей, чем соперник (2000, Буш<Гора)
Роль «колеблющихся штатов» и неравенство избирателей (Флорида, Нью-Мексико vs Юта)
Выборы-2008 (http://edition.cnn.com/election/2008/):
Обама (66,9 млн.) vs МакКейн (58,3 млн.)
победа МакКейна – смена позиции 0,4 млн. или 26,1 млн.(12% голосов) «нужных людей»
Парадокс Алабамы; парадокс новых штатов; парадокс более быстрого роста населения…
Слайд 4Правило Кондорсе vs Борда
Правило относительного большинства:
3 5 7 6
A A B C A – победитель в
Правило Кондорсе vs Борда
Правило относительного большинства:
3 5 7 6
A A B C A – победитель в

B C D B A – наихудший кандидат (13 голосов из 21)
C B C D C >A (13 из 21), C > B (11 из 21), C > D (14 из 21) ⇒ победитель C
D D A A B > C: 1 место (7:6), 1–2 м (16:11), 1–3 м (21:21) ⇒ победитель B
Правило Борда (учет рангов кандидатов):
Кандидаты от худшего к лучшему получают ранги 0 → 1 → 2 → 3 → …
Победитель по Борда – кандидат с максимальной суммой очков.
Правило Кондорсе:
Победитель по Кондорсе – кандидат, побеждающий любого из соперников при парном сравнении.
Обобщение правила Борда: произвольные шкалы
Правило относительного большинства – 0 0 … 0 1.
Правило антибольшинства – 0 1 … 1 1.
Слайд 5Парадокс Кондорсе
Победитель по Кондорсе может отсутствовать: К > П > Ч >
Парадокс Кондорсе
Победитель по Кондорсе может отсутствовать: К > П > Ч >
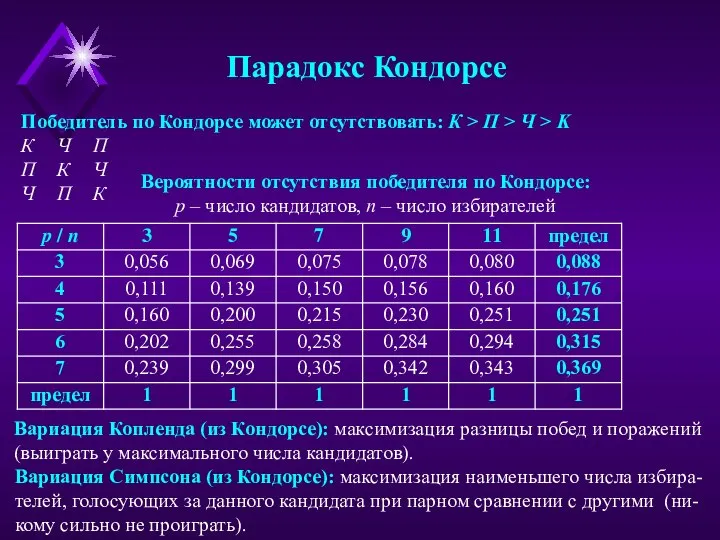
К Ч П
П К Ч
Ч П К
Вероятности отсутствия победителя по Кондорсе:
p – число кандидатов, n – число избирателей
Вариация Копленда (из Кондорсе): максимизация разницы побед и поражений
(выиграть у максимального числа кандидатов).
Вариация Симпсона (из Кондорсе): максимизация наименьшего числа избира-телей, голосующих за данного кандидата при парном сравнении с другими (ни-кому сильно не проиграть).
Слайд 6Борда ≠ Кондорсе
Пример для строго монотонного правила подсчета очков :
3 2 1 1
s2 A B B C
Борда ≠ Кондорсе
Пример для строго монотонного правила подсчета очков :
3 2 1 1
s2 A B B C

s1 B C A A очки B = = очки A
s0 C A C B
Существуют профили предпочтений избирателей, при которых победитель
по Кондорсе не может быть избран ни при каком методе подсчета очков!
Пример для произвольного правила подсчета очков :
6 4 4 3
s2 A B B C A > B (9 из 17), A > C (10 из 17) ⇒ A – победитель по Кондорсе
s1 B C A A очки B = = очки A
s0 C A C B
Слайд 7Профиль Страффина
4 1 3
A C E E
B D A A
C B D B
D E B D
E A C C
Победитель по Кондорсе отсутствует,
у всех
Профиль Страффина
4 1 3
A C E E
B D A A
C B D B
D E B D
E A C C
Победитель по Кондорсе отсутствует,
у всех

Вариация Копленда:
победитель A (+3–1)
B=C=D (+2–2), E (+1–3).
Вариация Симпсона:
победители B=C=D=E (4), A (1).
Правило Борда – классическое и случай произвольных шкал. Победителем может стать любой из кандидатов.
4 A=1*4+4*0+1*3+3*3=16
3 B=1*3+4*2+1*1+3*2=18
2 С=1*2+4*4+1*0+3*0=18
1 D=1*1+4*3+1*2+3*1=18
0 E=1*0+4*1+1*4+3*4=20
4 A=19,6
3,9 B=18,9
2 С=18
1 D=21,6
0 E=20
4 A=19,6
3 B=18
2 С=21,6
1 D=18
0,9 E=20,9
4 A=16
3 B=24,3
2,9 С=18,9
1 D=18,9
0 E=20
9 A=41
8 B=23
2 С=38
1 D=38
0 E=40
Слайд 8Аксиоматический подход
Однозначность – правило всегда дает сделать однозначный выбор. Не вы-полняется для
Аксиоматический подход
Однозначность – правило всегда дает сделать однозначный выбор. Не вы-полняется для

Анонимность (равноправие избирателей) – имена избирателей не имеют значения: если два избирателя поменяются голосами, то результат выборов не изменится. Не выполняется, если при равенстве победителем становится выбранный определенным избирателем.
Нейтральность (равноправие альтернатив) – имена кандидатов не имеют значения: если поменять местами кандидатов A н B в предпочтении каждого избирателя, то исход голосования изменится соответственно. Не выполняет-ся, если при равенстве победителем становится определенный кандидат.
Состоятельность по Кондорсе – правило всегда выбирает победителя по Кондорсе, если он существует. Не выполняется для любых методов подсчета очков, в т.ч. для правила относительного большинства, правила Борда и т.д.
Парето-эффективность (единогласие) – если кандидат A для всех избира-телей лучше B, то B не может быть избранным. Не выполняется для правила антибольшинства.
Слайд 9Последовательные сравнения
по правилу большинства
1. Не выполняется нейтральность. Повестка определяет контроль над выборами.
Побед.
Последовательные сравнения
по правилу большинства
1. Не выполняется нейтральность. Повестка определяет контроль над выборами.
Побед.

A A D D B A>B, A>C,
B B B C C B>C, В>D,
C C A A D C>D, D>A.
D D C B A
2. Не выполняется Парето-эффективность.
B A C D D C C
A D B A
C B D для всех избирателей
A A D D
C C A A A>B, C>D, A>C (при равенстве голосов)
B B B B при этом D>A для всех избирателей
Слайд 10Аксиоматический подход
Монотонность – увеличившаяся поддержка кандидата не может уменьшить шанса быть избранным.
Аксиоматический подход
Монотонность – увеличившаяся поддержка кандидата не может уменьшить шанса быть избранным.

профиль 1: профиль 2:
6 5 4 2 6 5 4 2 Профиль 1: выходят A и B, A > B (11:6)
A C B B A C B A Профиль 2: A улучшает свое положение,
B A C A B A C B выходят A и C, C > A (9:8).
C B A C C B A C
Не выполняется для правила альтернативных голосов (последовательного ис-ключения неудачников) для любого способа подсчета очков.
6 4 6 2 6 3 Шаг 1: исключается C,
s2 A B B C C A
s1 B A C B A C Шаг 2: A > B (15:12).
s0=0 C C A A B B
9 1 6 8 3 В выделенных столбцах A становится лучше B
s2 A B B C A Шаг 1: исключается B,
s1 B A C A C
s0=0 C C A B B Шаг 2: C > A (14:13).
Слайд 11Аксиоматический подход
Пополнение – если 2 независимые группы избирателей выбирают кандида-та A, то,
Аксиоматический подход
Пополнение – если 2 независимые группы избирателей выбирают кандида-та A, то,

Состоятельный по Кондорсе метод выбирает A в группе 1, при этом B>A
Гр.1: Гр. 2:
2 2 2 4 3 Гр.1: победитель A. AC (4:2), B<С (2:4).
C A B A B Гр.2: победитель A. A>B (4:3), A>C (7:0), B>С (7:0).
B C A B A Гр.1+2: победитель B. AC (11:2), B>С (9:4).
A B C C C
Участие – собственный бюллетень не может уменьшит полезность избира-теля. Не выполняется для любого правила, состоятельного по Кондорсе, при 4 и более кандидатах.
3 3 5 4 4
A A D B C Правило Симпсона до участия: победитель A.
D D B C A S(A)=6(B,C), S(B)=4(D), S(C)=3(B), S(D)=5(A).
C B C A B Правило Симпсона после участия: победитель B.
B C A D D S(A)=6(C), S(B)=8(D), S(C)=7(D), S(D)=5(A).
Слайд 12Аксиоматический подход
Неманипулируемость (независимость от посторонних альтернатив) – нельзя увеличить свою полезность, ведя
Аксиоматический подход
Неманипулируемость (независимость от посторонних альтернатив) – нельзя увеличить свою полезность, ведя

2 2 Избиратели с профилем C > B > A видят, что C не побеждает ни
A B C при каких обстоятельствах и стратегически голосуют B > C > A.
B A B В результате от положения C меняется победитель голосования.
C C A
Разрешение проблемы:
Вероятностные правила голосования.
Пример: «Правило случайного диктатора» – вероятностная версия относительного большинства. Доминирующая стратегия – указать наи-лучшего для себя кандидата. Не выполняется «Парето-эффективность».
Ограничение области предпочтений
Пример: «однопиковые предпочтения» – предпочтения, для которых при линейном упорядочении кандидатов полезность сначала возрастает до некоторого пика, а затем уменьшается.
Слайд 13Случай однопиковых предпочтений
Коллективный выбор температуры в комнате (открыть / закрыть окно)
Из двух
Случай однопиковых предпочтений
Коллективный выбор температуры в комнате (открыть / закрыть окно)
Из двух

Экономическая свобода
24>26 (4:1), 22>24 (3:2), 21>22 (3:2)
Упорядочение не обязательно должно быть изначально. Можно придумать порядок, при котором предпочтения однопиковые!
ЦСКА, Локомотив, Спартак
Слайд 14ЦСКА, Локомотив, Спартак
Л Л С Ц С Ц У Локомотива при игре с ЦСКА и Спартаком
С Ц Л Л Ц С двойная
ЦСКА, Локомотив, Спартак
Л Л С Ц С Ц У Локомотива при игре с ЦСКА и Спартаком
С Ц Л Л Ц С двойная

Ц С Ц С Л Л
2000 – Локомотив во внутригрупповом выше Спартака, хотя в чемпионате
Спартак по-прежнему (как и в 90-е) победитель с большим отрывом.
2001-2004, 2008 – одинаковые результаты в чемпионате и в турнире 3 команд.
2005-2006 (!!!) – Локомотив лучший в группе, хотя худший в чемпионате
2007 – Локомотив существенно хуже остальных в чемпионате, но второй в группе с большим опережением Спартака и рядом с 1 местом ЦСКА.
Сопоставление результатов в турнире троих и в чемпионате:
Неограниченная область предпочтений приводит
к стратегическому поведению и плохим для всех исходам
для любых правил голосования!
Слайд 15Выполнение аксиом
для различных правил голосования
О – относительное большинство
Б – правило Борда
A –
Выполнение аксиом
для различных правил голосования
О – относительное большинство
Б – правило Борда
A –
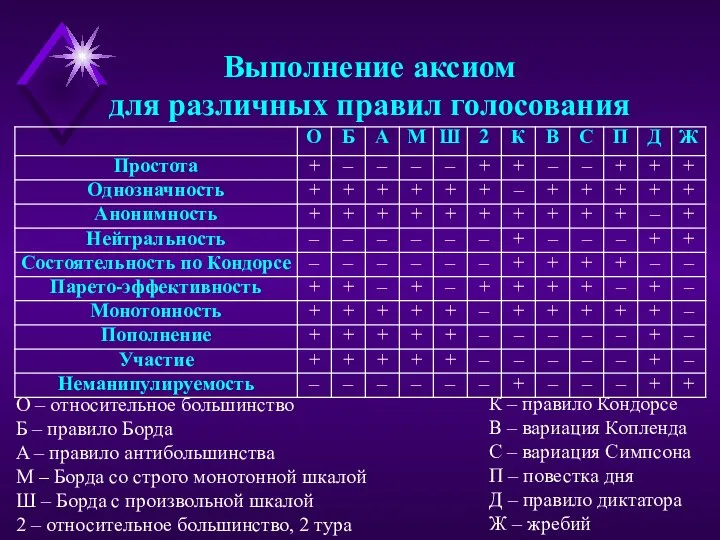
М – Борда со строго монотонной шкалой
Ш – Борда с произвольной шкалой
2 – относительное большинство, 2 тура
К – правило Кондорсе
В – вариация Копленда
С – вариация Симпсона
П – повестка дня
Д – правило диктатора
Ж – жребий
Слайд 16Теорема Эрроу
N={1,2,…,n} – избиратели, A={a,b,c,…} – кандидаты.
P(A) – множество линейных порядков на
Теорема Эрроу
N={1,2,…,n} – избиратели, A={a,b,c,…} – кандидаты.
P(A) – множество линейных порядков на

R(A) – множество нестрогих порядков на A
Более сложная задача – не просто найти победителя, но составить порядок
P(A)n→R(A)
Если |A|=2, есть единственное анонимное, нейтральное и монотонное правило –правило большинства. Оно также является неманипулируемым.
Теорема Эрроу о невозможности демократии: если |A|>2, существует единст-венное Парето-эффективное неманипулируемое правило – правило диктатора.
4 Л Ц С С=Л=Ц=9 Л Ц С Д=9
3 С Л Ц Д=3 Д Д Д М=6
2 Ц С Л М=0 М М М Л=Ц=С=5
1 Д Д Д С Л Ц
0 М М М Ц С Л
Пример стратегического поведения, приводящего к плохому для всех исходу,
для правила Борда:
Слайд 17Метод Шульце (1997)
(метод разъезженного пути)
Избиратели указывают в бюллетене предпочтения относительно кандидатур. 1
Метод Шульце (1997)
(метод разъезженного пути)
Избиратели указывают в бюллетене предпочтения относительно кандидатур. 1

Разрешается ставить одинаковые числа нескольким кандидатурам.
Разрешается вообще не заполнять поле для части кандидатур (в таком случае считается, что они одинаково хуже всех, для которых указано число).
Обработка результатов голосования:
d(A,B) – число избирателей, строго предпочитающих кандидата A кандидату B.
Путь силы p от A до B – последовательность кандидатов C(1),…,C(n) со св-ми:
C(1)=A, C(n)=B.
d(C(i),C(i+1)) > d(C(i+1),C(i)), i=1,…,n.
p=min d(C(i),C(i+1)).
Сила сильнейшего пути p(A,B) – максимальное значение силы пути от A до B.
Если пути от кандидата A к кандидату B не существует, p(A,B)=0.
Победитель – кандидат A, такой что p(A,B) ≥ p(B,A) для каждого кандидата B.
Слайд 18Метод Шульце (1997). Пример
45 избирателей, 5 кандидатов:
5 5 8 3 7 2 7 8
A A B C C C D E
C D E A A B C B
B E D B E
Метод Шульце (1997). Пример
45 избирателей, 5 кандидатов:
5 5 8 3 7 2 7 8
A A B C C C D E
C D E A A B C B
B E D B E
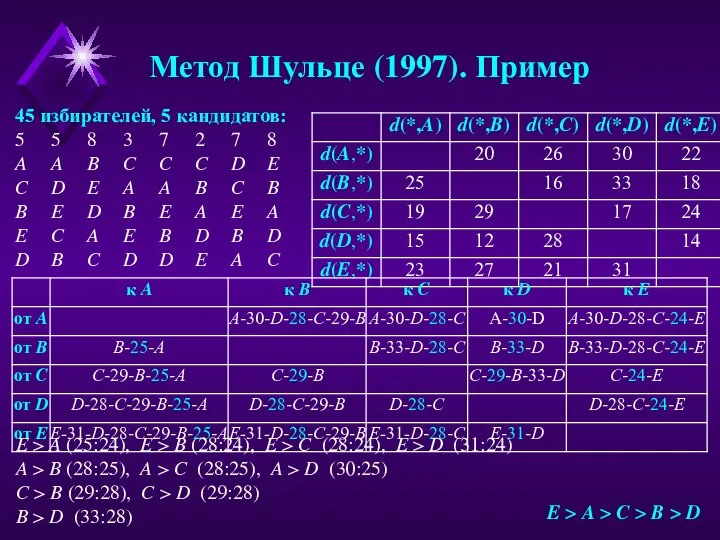
E C A E B D B D
D B C D D E A C
E > A (25:24), E > B (28:24), E > C (28:24), E > D (31:24)
A > B (28:25), A > C (28:25), A > D (30:25)
C > B (29:28), C > D (29:28)
B > D (33:28)
E > A > C > B > D
Слайд 19Метод Шульце. Еще примеры
Кондорсе:
23 17 2 10 8
A B B C C
B C A A B
C A C B A
B > A
Метод Шульце. Еще примеры
Кондорсе:
23 17 2 10 8
A B B C C
B C A A B
C A C B A
B > A
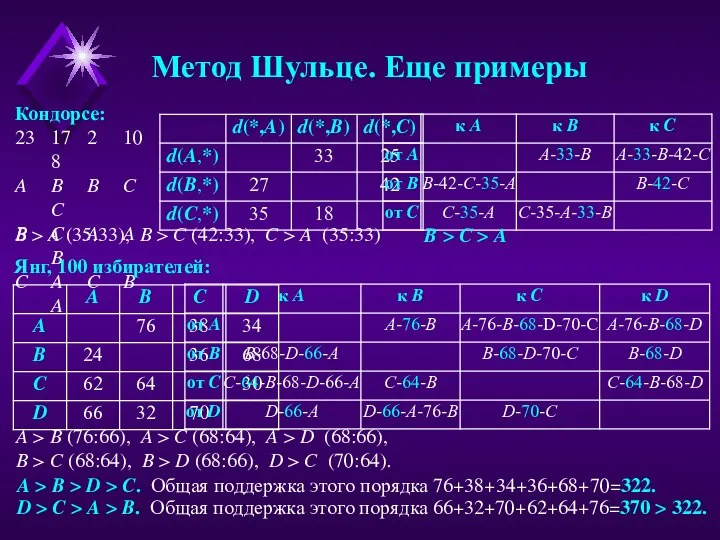
B > C > A
Янг, 100 избирателей:
A > B (76:66), A > C (68:64), A > D (68:66),
B > C (68:64), B > D (68:66), D > C (70:64).
A > B > D > C. Общая поддержка этого порядка 76+38+34+36+68+70=322.
D > C > A > B. Общая поддержка этого порядка 66+32+70+62+64+76=370 > 322.
 Спрос и предложение
Спрос и предложение Основные тренды на рынке производства печатной продукции
Основные тренды на рынке производства печатной продукции Концепция рыночной экономики
Концепция рыночной экономики Подготовка к ОГЭ по обществознанию (занятие 7)
Подготовка к ОГЭ по обществознанию (занятие 7) Изменения на транспорте ЕС (Женева 2018)
Изменения на транспорте ЕС (Женева 2018) Моя будущая профессия - экономист
Моя будущая профессия - экономист Webinarium Kwalifikacje rynkowe a szkolnictwo branżowe
Webinarium Kwalifikacje rynkowe a szkolnictwo branżowe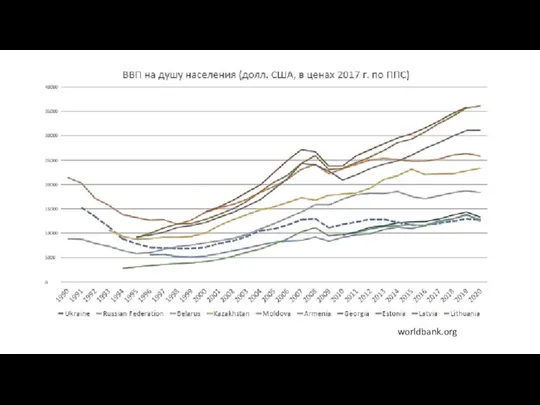 ВВП на душу населения (долл. США, в ценах 2017 г. по ППС)
ВВП на душу населения (долл. США, в ценах 2017 г. по ППС) Сущность и типы валютной политики Выполнила: Клеутина С.А.
Сущность и типы валютной политики Выполнила: Клеутина С.А. Теория экономического роста
Теория экономического роста Роль государства
Роль государства Регулирование международных миграционных процессов
Регулирование международных миграционных процессов Экономика и человек
Экономика и человек …..- Это Совокупность наиболее крупных товарных бирж мира, через которые проходит основной объем торговли между странами.
…..- Это Совокупность наиболее крупных товарных бирж мира, через которые проходит основной объем торговли между странами. Теория затрат. Рыночное предложение
Теория затрат. Рыночное предложение Роль экономики в жизни общества. Параграф 1
Роль экономики в жизни общества. Параграф 1 радиционная предметная неделя истории, обществознания, экономики и права Экология истории, экология памяти 16-21 января
радиционная предметная неделя истории, обществознания, экономики и права Экология истории, экология памяти 16-21 января Подборка фразеологизмов и пословиц по экономическому воспитанию дошкольников
Подборка фразеологизмов и пословиц по экономическому воспитанию дошкольников Макроэкономика: Мировые тренды
Макроэкономика: Мировые тренды Экономика труда : планирование фонда оплаты труда структурных подразделений предприятия
Экономика труда : планирование фонда оплаты труда структурных подразделений предприятия Финансовая система государства: особенности построения, состав и характеристика звеньев
Финансовая система государства: особенности построения, состав и характеристика звеньев Экономика
Экономика Буржуазная демократия как форма диктатуры буржуазии
Буржуазная демократия как форма диктатуры буржуазии Предпринимательская этика и этикет
Предпринимательская этика и этикет Национальные счета. ВВП
Национальные счета. ВВП Экономика труда. Структура общественного труда
Экономика труда. Структура общественного труда Концепция установления прожиточного минимума и минимального размера оплаты труда
Концепция установления прожиточного минимума и минимального размера оплаты труда Кривая производственных возможностей
Кривая производственных возможностей