სიგნალის მათემატიკური წარმოდგენა

სიგნალის მათემატიკური წარმოდგენა
ვექტორებს შორის კავშირი – სკალარული ნამრავლი..
r სიდიდეს ეწოდება კორელაციის კოეფიციენტი.

სიგნალის მათემატიკური წარმოდგენა

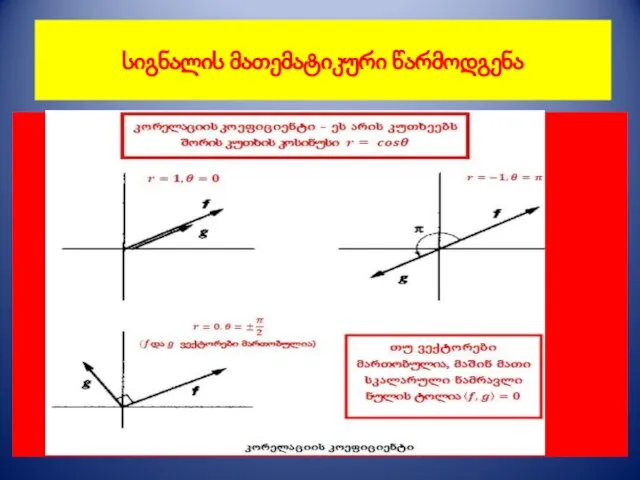
სიგნალის მათემატიკური წარმოდგენა
კორელაციის კოეფიციენტი:
დამოკიდებულია ვექტორებს შორის კუთხეზე;
არაა დამოკიდებული ვექტორების ნორმაზე.
სკალარული ნამრავლი ვექტორის კომპონენტებით:

ორთონორმირებული ბაზისი
ორი ვექტორის ურთიერთმართობული წყვილი – ორთოგონალური ბაზისი.
–ორთონორმირებული ბაზისი.
ვექტორი, რომლის ნორმა 1-ის ტოლია–ერთეულოვანი ვექტორი.
ერთეულოვანი ვექტორის სიგრძე ერთი
ერთეულის რიგისაა.

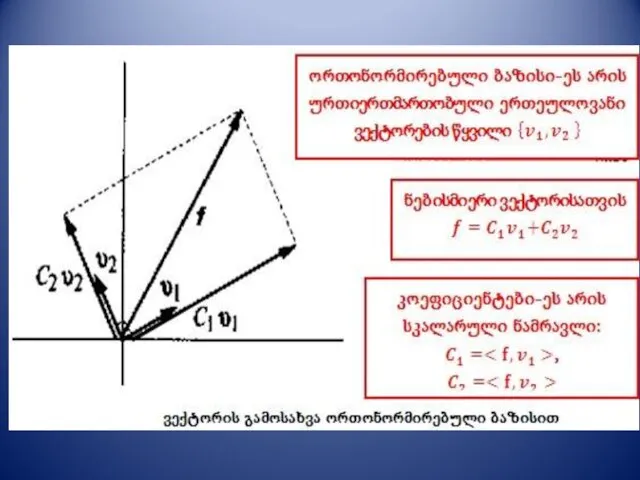
ორთონორმირებული ბაზისი
ორთონორმირებული ბაზისი - ურთიერთმართობული ერთეულოვანი ვექტორების წყვილი, რომლებიც პარამეტრების წყვილთან ერთობლიობაში გვაძლევენ ვექტორის სიდიდეს

ორთონორმირებული ბაზისი
გამოვსახოთ f ვექტორი ორთონორმირებული ბაზისითა და კოეფიციენტებით
შესაკრებები - f ვექტორის პროექციებია,ხოლო
,

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
სამგანზომილებიანი ვექტორის სივრცეში
N განზომილებიანი სივრცისათვის-
უსასრული განზომილების სივრცის ანუ ფუნქციის სივრცისათვის-ნორმა განსაზღვრულ შუალედში:
(N განზომილებიანი ვექტორის
ნორმის განზოგადება)

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
რაც დიდია ინტერვალი მოც. ფორმულაში, მოსახერხებელია ფუნქციის ნორმის ნორმირება ინტერვალის სიგრძის მიმართ:
მრავალვექტორიანი ნორმის შემთხვევაში:

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
თუ შევადარებთ ფუნქციის ნორმისა და ვექტორის ნორმის ფორმულებს, ცხადი იქნება შემდეგი შესაბამისობა:
N განზომილებიანი სივრცისათვის-
.

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
f ვექტორის სიდიდე (აბსოლუტური მნიშვნელობა) - უწოდებენ ვექტორის ნორმას.
ორ ვექტორს შორის მანძილი ვექტორის კომპონენტების გამოყენებით:

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
ვექტორებს შორის კავშირი – სკალარული ნამრავლი..
r სიდიდეს ეწოდება კორელაციის კოეფიციენტი.

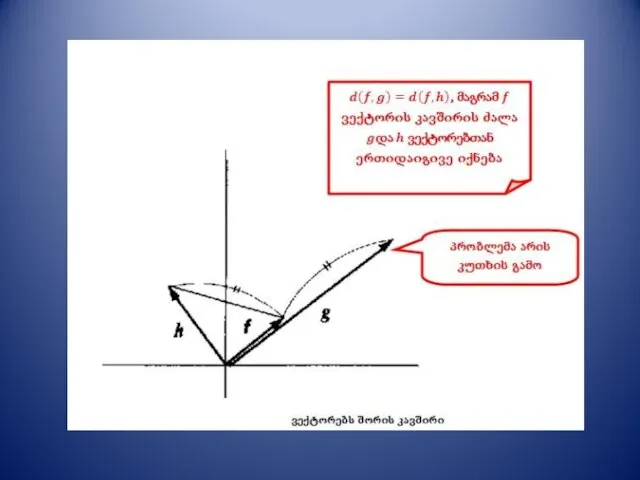
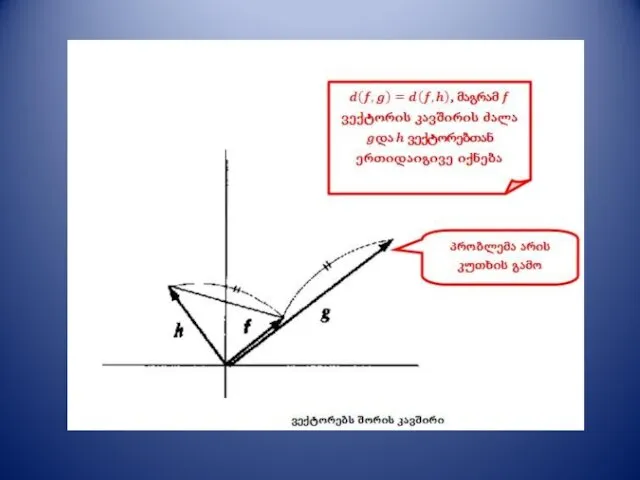
ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
მანძილი ორ ფუნქციას შორის მოცემულ ინტერვალზე - ვექტორი იცვლება ფუნქციით, ხოლო ჯამი-ინტეგრალით

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
შემდეგი ეტაპი - სკალარული ნამრავლის განსაზღვრა.
ვექტორების სკალარული ნამრავლი გამოითვლება ასე
N განზომილებიან სივრცეში ვექტორების სკალარული ნამრავლი :

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
ვექტორების მდგენელების გათვალისწინებით
ამ გამოსახულებიდან შეიძლება მივიღოთ კორელაციის კოეფიციენტი N განზომილე ბიან სივრცეში:

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
ვექტორი ფუნქცია, ჯამი ინტეგრალი - შესაბამისობის გამოყენებით, ორი ფუნქციის სკალარული ნამრავლი [a,b] ინტერვალზე:
ფუნქციის სკალარული ნამრავლი თავისთავზე:

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
ფუნქციას აქვს იგივე თვისებები, რაც მრავალგანზომილებიან ვექტორს ვექტორულ სივრცეში.
ფუნქციის სკალარული ნამრავლის განსაზღვრა ნიშნავს ფუნქციებს შორის კუთხის ცნების შემოტანას.

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
ფუნქციათა სივრცეში კორელაციის კოეფიციენტი განისაზღვრება, როგორც ვექტორებისათვის:

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
სხვაგვარად:

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
დამოკიდებულება რთული ხასიათისაა, ხოლო პრინციპი იგივეა, რაც ვექტორების შემთხვევაში.
კორელაციის კოეფიციენტი გვიჩვენებს ფუნქციის „მსგავსების“ ხარისხს. ღებულობს მნიშვნელობებს -1 - დან 1-მდე

ვექტორული სივრციდან ფუნქციის სივრცეზე გადასვლა
მაშასადამე:
სკალარული ნამრავლით შეიძლება ფუნქციებს შორის კუთხის განსაზღვრა;
ფუნქციების ურთიერთმართობულობის განსაზღვრა (ვექტორებს შორის ურთიერთმართობულობის მსგავსად).