Содержание
- 2. 1. Планеты движутся по эллипсам, в одном из фокусов которого находится Солнце. 2. Радиус-вектор планеты за
- 3. Эта сила называется гравитационной (или силой всемирного тяготения). Силы тяготения всегда являются силами притяжения и направлены
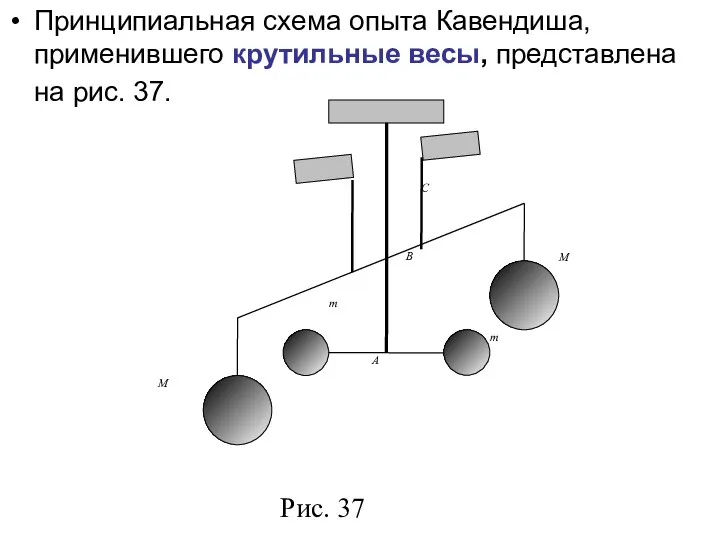
- 4. Принципиальная схема опыта Кавендиша, применившего крутильные весы, представлена на рис. 37.
- 5. § 23. Сила тяжести и вес. Невесомость На любое тело, расположенное вблизи Земли, действует сила тяготения
- 6. Если пренебречь суточным вращением Земли вокруг своей оси, то сила тяжести и сила гравитационного тяготения равны
- 7. Весом тела называют силу, с которой тело вследствие тяготения к Земле действует на опору (или подвес),
- 8. Если тело движется в поле тяготения Земли с ускорением , то к этому телу приложена дополнительная
- 9. § 24. Поле тяготения и его напряженность Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения,
- 10. Напряженность поля тяготения определяется силой, действующей со стороны поля на материальную точку единичной массы, и совпадает
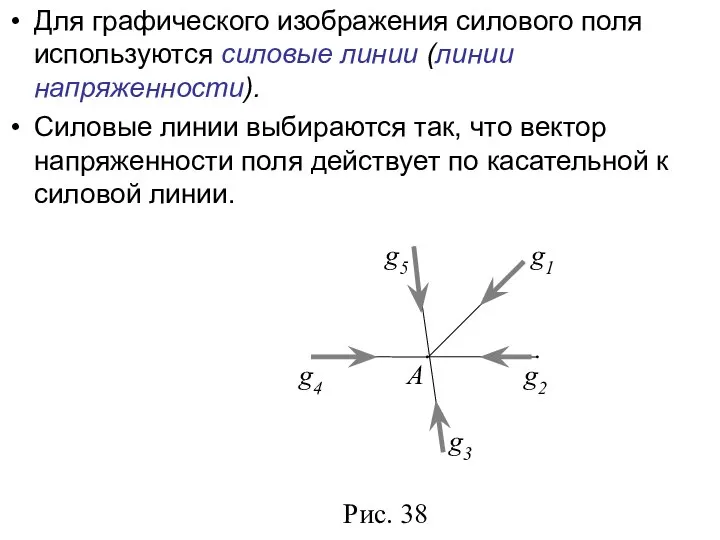
- 11. Для графического изображения силового поля используются силовые линии (линии напряженности). Силовые линии выбираются так, что вектор
- 12. § 25. Работа в поле тяготения. Потенциал поля тяготения Вычислим, какую надо затратить работу для удаления
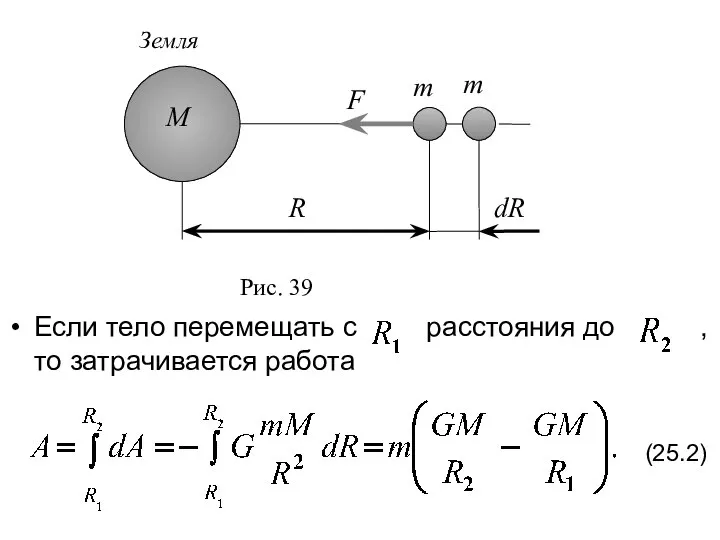
- 13. Если тело перемещать с расстояния до , то затрачивается работа (25.2)
- 14. Из формулы (25.2) вытекает, что затраченная работа в поле тяготения не зависит от траектории перемещения, а
- 15. В формулы входит только разность потенциальных энергий в двух состояниях, поэтому для удобства принимают потенциальную энергию
- 16. Потенциал поля тяготения — скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля
- 17. Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными. Из выражений (25.1) и (25.4) следует, что элементарная
- 18. Величина характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения. Можно показать, что
- 19. В качестве частного примера, исходя из представлений теории тяготения, рассмотрим потенциальную энергию тела, находящегося на высоте
- 20. § 26. Космические скорости Для запуска ракет в космическое пространство надо в зависимости от поставленных целей
- 21. На спутник, движущийся по круговой орбите радиусом, действует сила тяготения Земли, сообщающая ему нормальное ускорение .
- 22. Второй космической (или параболической) скоростью называют ту наименьшую скорость, которую необходимо сообщить телу, чтобы оно могло
- 23. Следовательно Третьей космической скоростью называют скорость, которую необходимо сообщить телу на Земле, чтобы оно покинуло пределы
- 24. § 27. Неинерциальные системы отсчета. Силы инерции Законы Ньютона выполняются только в инерциальных системах отсчета. Системы
- 25. (27.1) где - ускорение в неинерциальной системе, - сила инерции, - ускорение в инерциальной системе). Т.е.
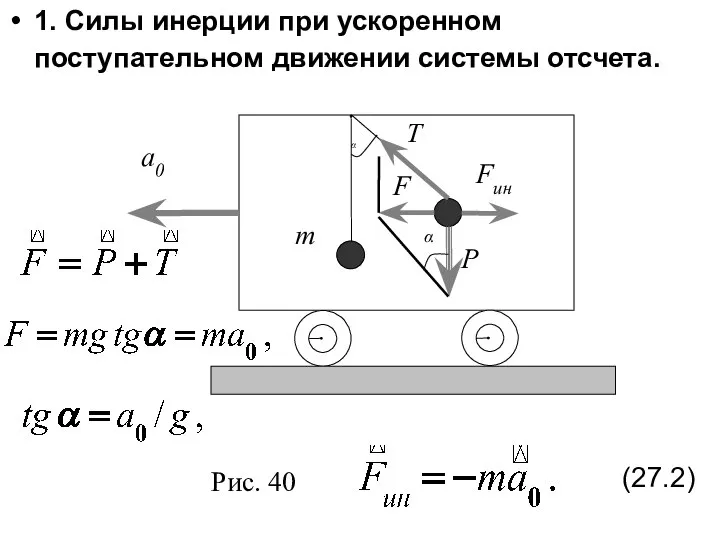
- 26. 1. Силы инерции при ускоренном поступательном движении системы отсчета. (27.2)
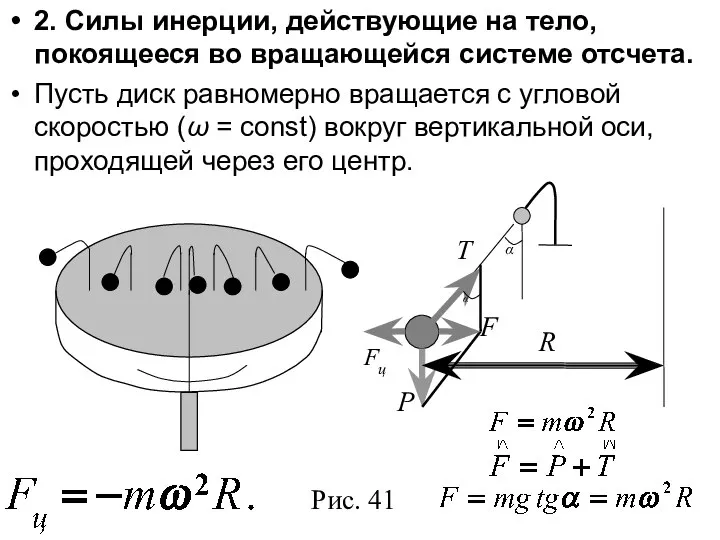
- 27. 2. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета. Пусть диск равномерно вращается с
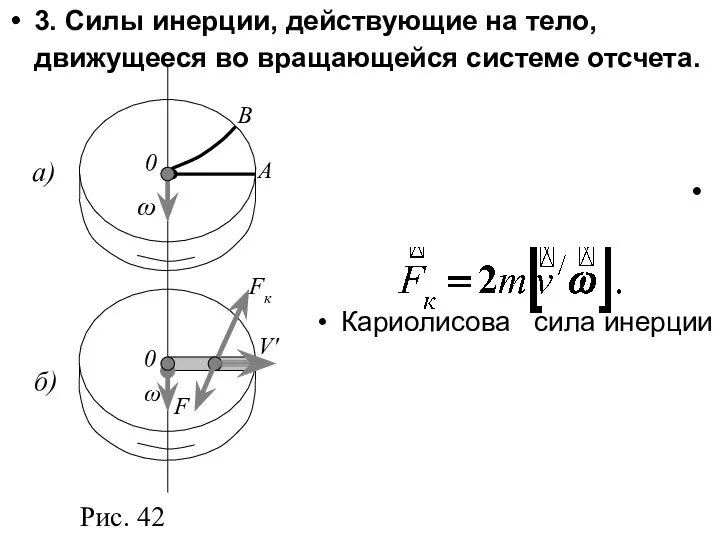
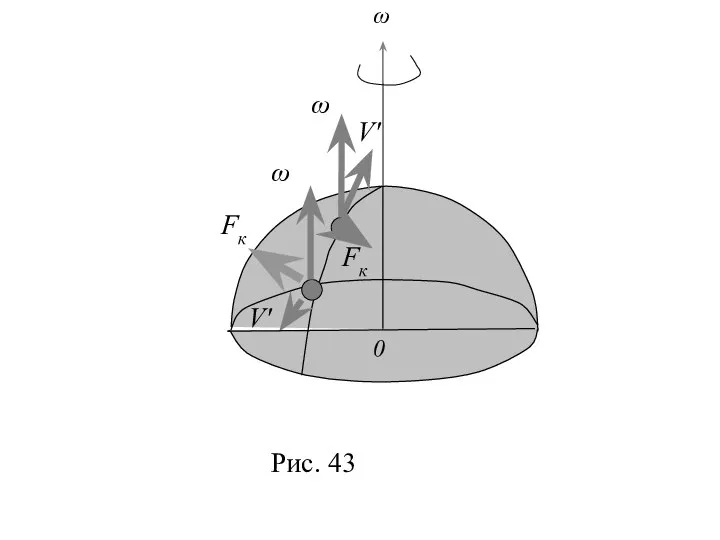
- 28. 3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета. Кариолисова сила инерции
- 30. Основной закон динамики для неинерциальных систем отсчета: Силы инерции вызываются не взаимодействием тел, а ускоренным движением
- 32. Скачать презентацию






















 Индивидуальное задание для практики (2)
Индивидуальное задание для практики (2) Презентация на тему Инфразвук
Презентация на тему Инфразвук  Презентация на тему Квантовая физика
Презентация на тему Квантовая физика  Эксплуатация аккумуляторов
Эксплуатация аккумуляторов Пара сил. Момент пары сил. Свойства пар сил. Момент силы относительно точки
Пара сил. Момент пары сил. Свойства пар сил. Момент силы относительно точки Организация технического обслуживания и диагностики с разработкой шиномонтажного стенда
Организация технического обслуживания и диагностики с разработкой шиномонтажного стенда Основы термодинамики. Тема № 4
Основы термодинамики. Тема № 4 Электрическая цепь. Последовательное и параллельное соединение проводников
Электрическая цепь. Последовательное и параллельное соединение проводников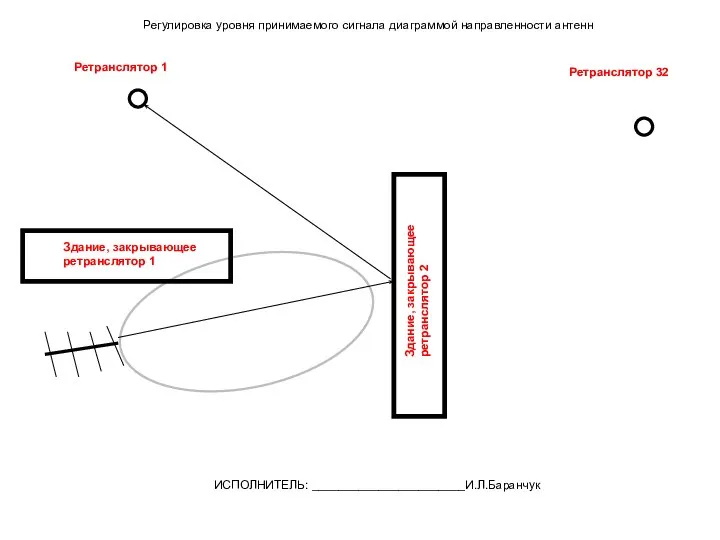 Приём отражённого сигнала в городе
Приём отражённого сигнала в городе Уравнение теплового баланса. Алгоритм решения задач
Уравнение теплового баланса. Алгоритм решения задач Плотность. Плотность мрамора
Плотность. Плотность мрамора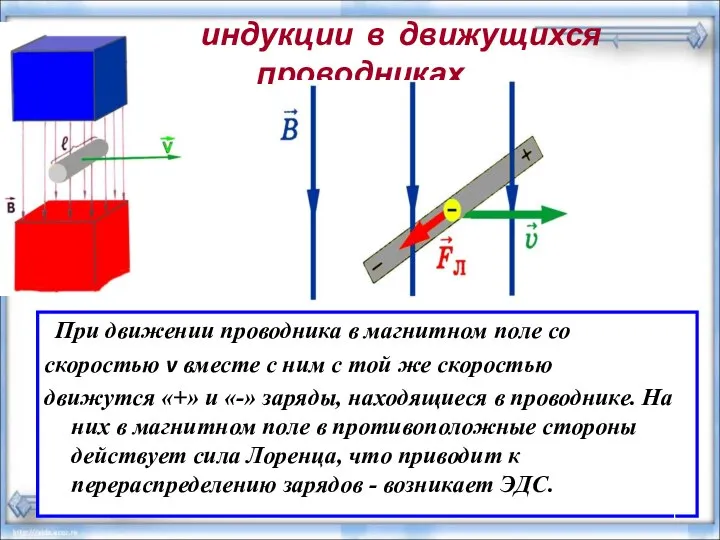 Вихревое электрическое поле. ЭДС индукции в движущихся проводниках
Вихревое электрическое поле. ЭДС индукции в движущихся проводниках График плавления и отвердевания кристаллических тел
График плавления и отвердевания кристаллических тел Звуки природы и звуки космоса. Что их объединяет
Звуки природы и звуки космоса. Что их объединяет Наглядное пособие для изучения шпоночного и штифтового соединений
Наглядное пособие для изучения шпоночного и штифтового соединений Техника безопасности при работе в лаборатории
Техника безопасности при работе в лаборатории Презентация на тему Перемещение при прямолинейном равноускоренном движении (9 класс)
Презентация на тему Перемещение при прямолинейном равноускоренном движении (9 класс)  Цепи переменного тока с последовательным соединением элементов
Цепи переменного тока с последовательным соединением элементов Уравнения Максвелла
Уравнения Максвелла Сила. Силы в природе и Работа. Мощность
Сила. Силы в природе и Работа. Мощность Метод размерностей
Метод размерностей Свет. Источники света. Звезда-Солнце. Солнечные и лунные затмения
Свет. Источники света. Звезда-Солнце. Солнечные и лунные затмения Инерционные силы
Инерционные силы Количество теплоты. Единицы количества теплоты. Удельная теплоемкость
Количество теплоты. Единицы количества теплоты. Удельная теплоемкость Тепловые двигатели
Тепловые двигатели Расчет силы тока и напряжения в электрических цепях
Расчет силы тока и напряжения в электрических цепях Lect_2
Lect_2 Давление света
Давление света