АЧХ и нуль-полюсная диаграмма

АЧХ и нуль-полюсная диаграмма
Фильтр хорошо подавляет частоты в узкой полосе вблизи частоты fs/4, т.е. является узкополосным режекторным фильтром.
Если увеличить задержку исходного фильтра в 4 и в 8 раз, то получим АЧХ и нуль-полюсные диаграммы, изображенные на рис.3 б.
Рис. 3 б

Передаточная функция
Обозначим передаточные функции рассмотренных элементарных нерекурсивных звеньев следующим образом:
H1(z) = 1 + z−1 ; H2(z) = 1 + z−2 ;
H4(z) = 1 + z−4 ; H8(z) = 1 + z−8.
Если включить эти звенья каскадно, то получим передаточную функцию
H(z) = (1 + z−1) (1 + z−2) (1 + z−4 ) (1 + z−8) (5).

Структурная схема и передаточная функция НЦФ
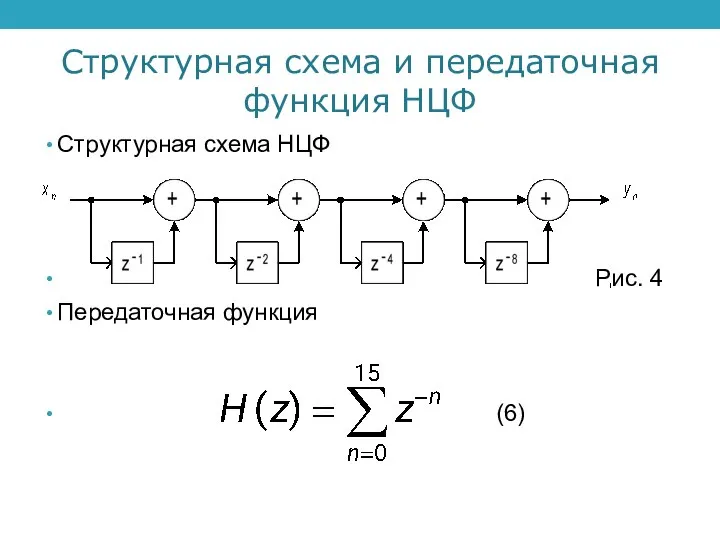
Структурная схема НЦФ
Рис. 4
Передаточная функция
(6)

Структурная схема ЦФ
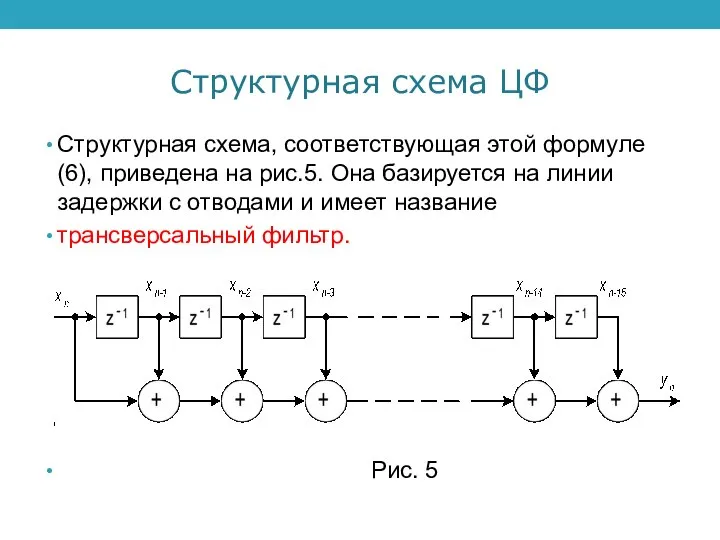
Структурная схема, соответствующая этой формуле (6), приведена на рис.5. Она базируется на линии задержки с отводами и имеет название
трансверсальный фильтр.
Рис. 5

Передаточная функция
Формула (6) представляет собой сумму геометрической прогрессии с показателем z−1 и может быть записана в виде
(7).
Если умножить числитель и знаменатель в (7) на z16 , то получим формулу для анализа положения нулей и полюсов:
.

Нули и полюса
Нуль-полюсная диаграмма для фильтра с передаточной функцией по формуле (7).
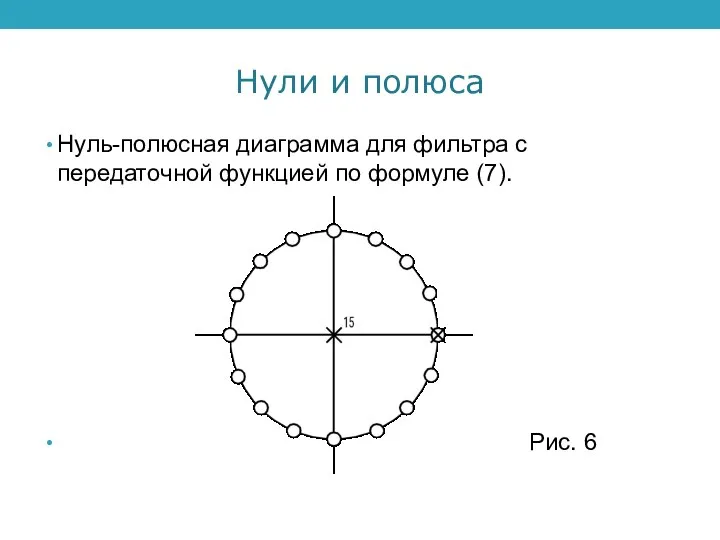
Рис. 6

Передаточная функция
Обобщая формулы (6) и (7) для фильтра N-го порядка, запишем:
(8),
(9).

Передаточная функция
АЧХ НЦФ N-го порядка
(10)

График АЧХ
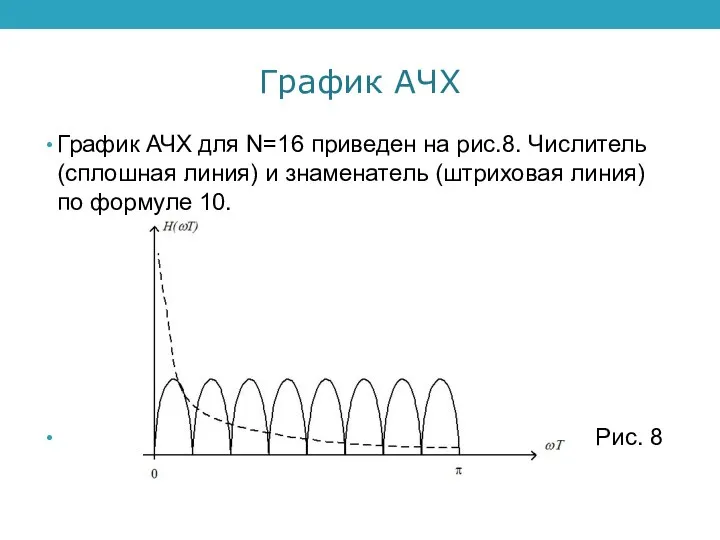
График АЧХ для N=16 приведен на рис.8. Числитель (сплошная линия) и знаменатель (штриховая линия) по формуле 10.
Рис. 8

График АЧХ
Неопределенность при ωT = 0 раскрываем по правилу Лопиталя:

График АЧХ
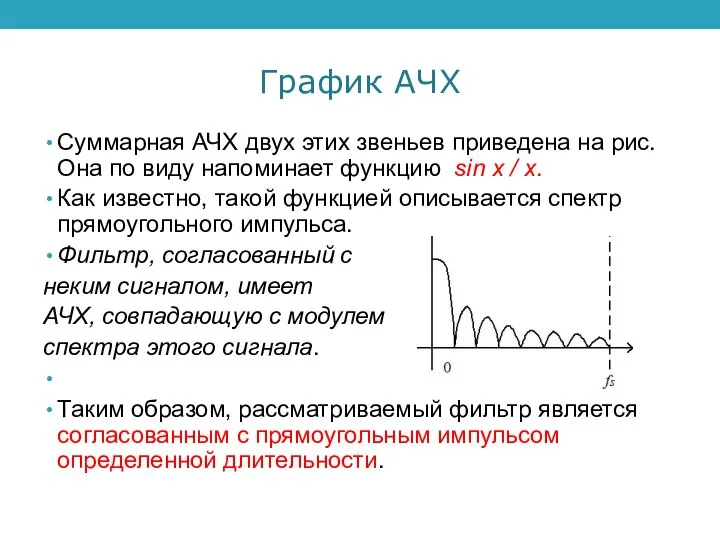
Суммарная АЧХ двух этих звеньев приведена на рис. Она по виду напоминает функцию sin x / x.
Как известно, такой функцией описывается спектр прямоугольного импульса.
Фильтр, согласованный с
неким сигналом, имеет
АЧХ, совпадающую с модулем
спектра этого сигнала.
Таким образом, рассматриваемый фильтр является согласованным с прямоугольным импульсом определенной длительности.

Согласованный фильтр
Тогда согласованный с этим импульсом фильтр должен иметь импульсную характеристику вида
(11)
Фильтр с передаточной функцией
как раз и обладает такой импульсной характеристикой.

Фильтр согласованный с прямоугольным импульсом длительностью NT
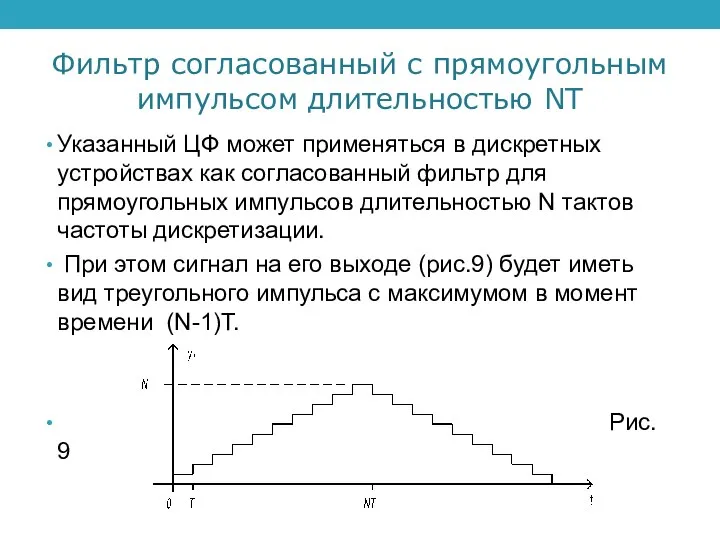
Указанный ЦФ может применяться в дискретных устройствах как согласованный фильтр для прямоугольных импульсов длительностью N тактов частоты дискретизации.
При этом сигнал на его выходе (рис.9) будет иметь вид треугольного импульса с максимумом в момент времени (N-1)T.
Рис. 9