Содержание
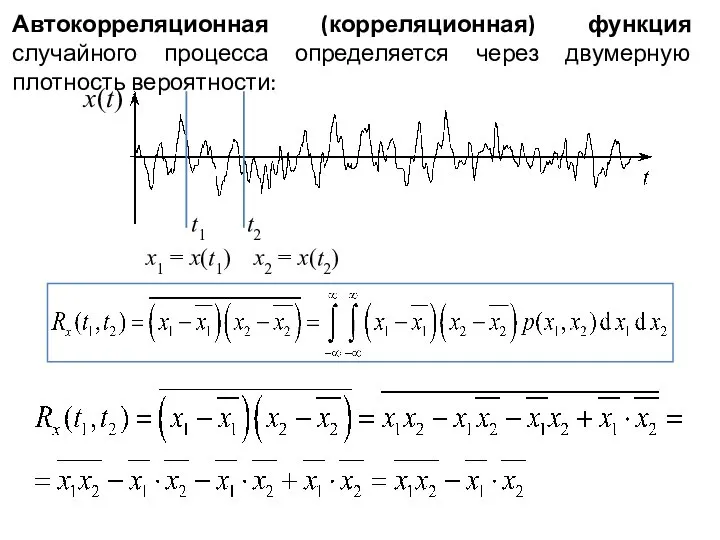
- 2. Автокорреляционная (корреляционная) функция случайного процесса определяется через двумерную плотность вероятности: t2 t1 x(t) x1 = x(t1)
- 3. Корреляционная функция стационарного случайного процесса: Нормированная корреляционная функция 1. Rx(–τ) = Rx(τ). 2. Rx(0) = σ2.
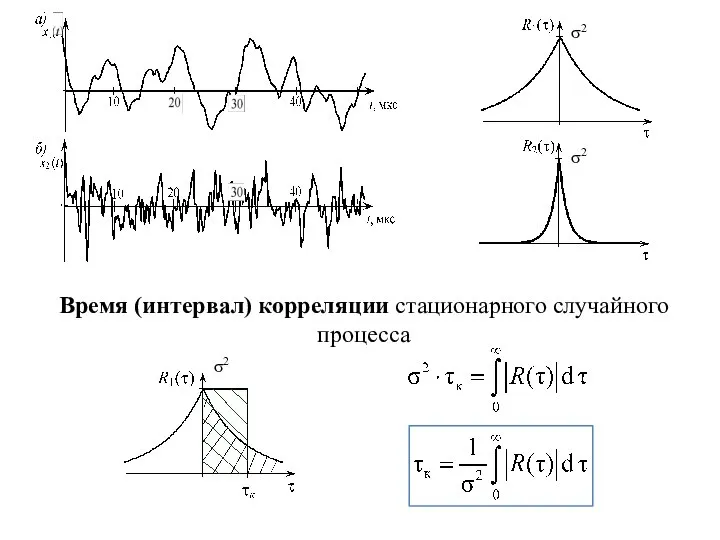
- 4. Время (интервал) корреляции стационарного случайного процесса σ2 σ2 σ2
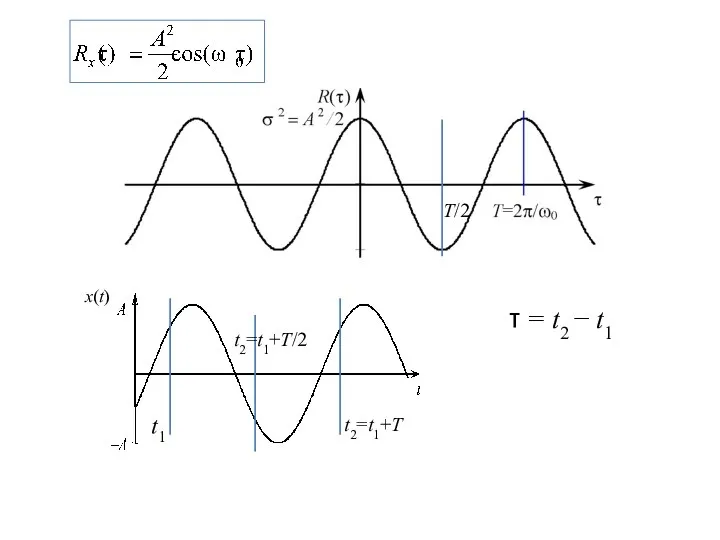
- 5. Корреляционная функция гармонического сигнала со случайной равномерно распределенной фазой
- 6. Корреляционная функция гармонического сигнала со случайной равномерно распределенной фазой
- 7. τ = t2 − t1 x(t) t2=t1+T t1 t2=t1+T/2 T/2
- 8. Взаимная корреляционная функция Характеризует корреляционную связь двух случайных процессов: x1 = x(t1), y2 = y(t2) Cлучайные
- 9. Если случайные процессы x(t) и y(t) независимы, то взаимно корреляционная функция равна нулю при любых значениях
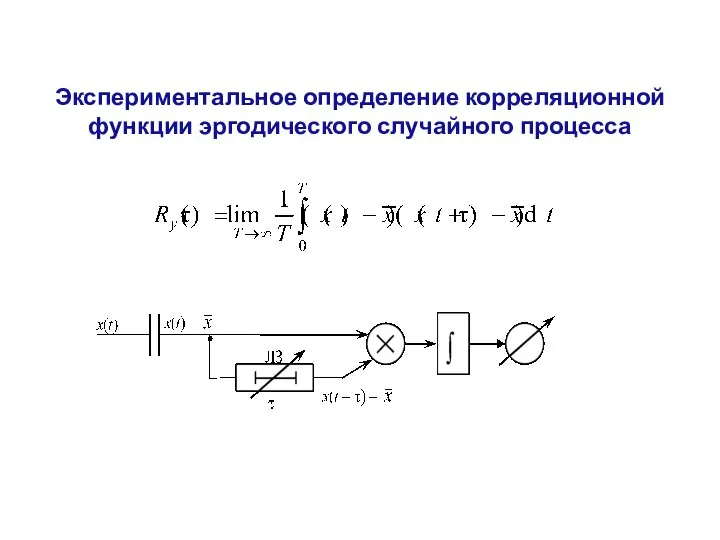
- 10. Экспериментальное определение корреляционной функции эргодического случайного процесса
- 11. Спектральная плотность мощности (спектр мощности, энергетический спектр) эргодического случайного процесса с Энергия реализации Средняя мощность реализации
- 12. Свойства энергетического спектра 1. W(ω) ≥ 0 3. W(–ω) = W(ω) 2. Теорема Винера - Хинчина
- 13. Односторонний спектр мощности (энергетический спектр) Эффективная ширина спектра
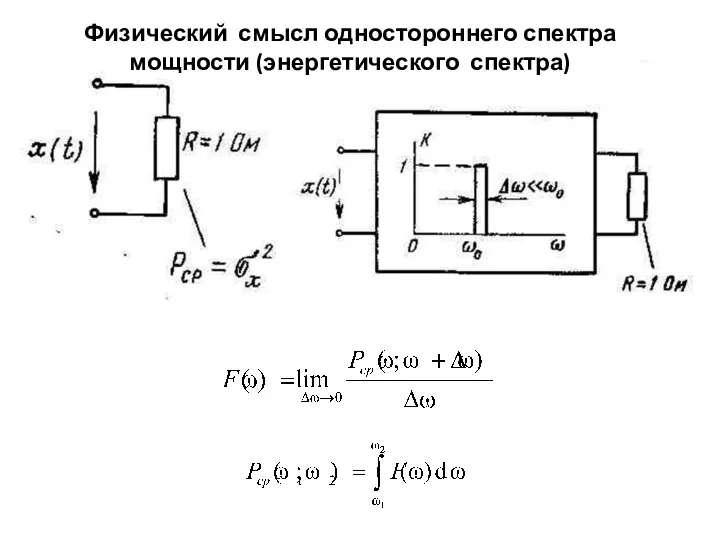
- 14. Физический смысл одностороннего спектра мощности (энергетического спектра)
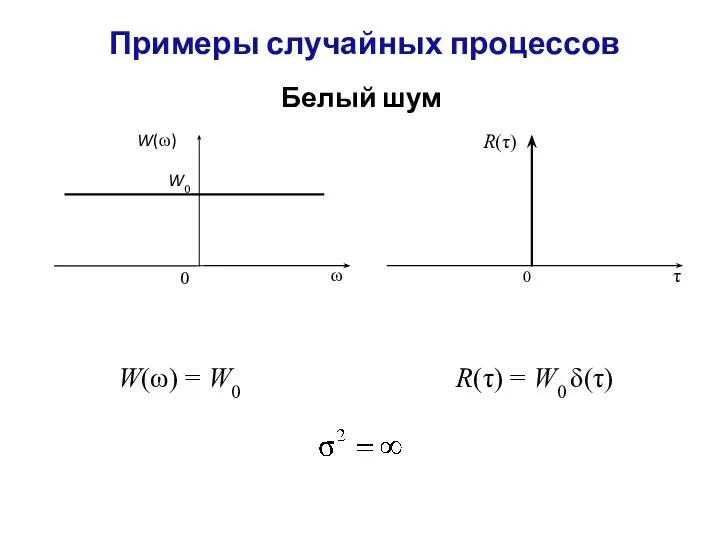
- 15. Примеры случайных процессов Белый шум R(τ) = W0 δ(τ) W(ω) = W0
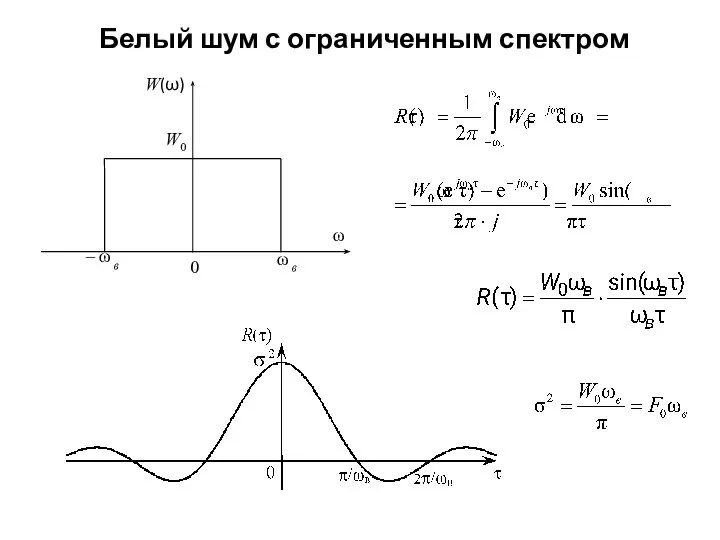
- 16. Белый шум с ограниченным спектром
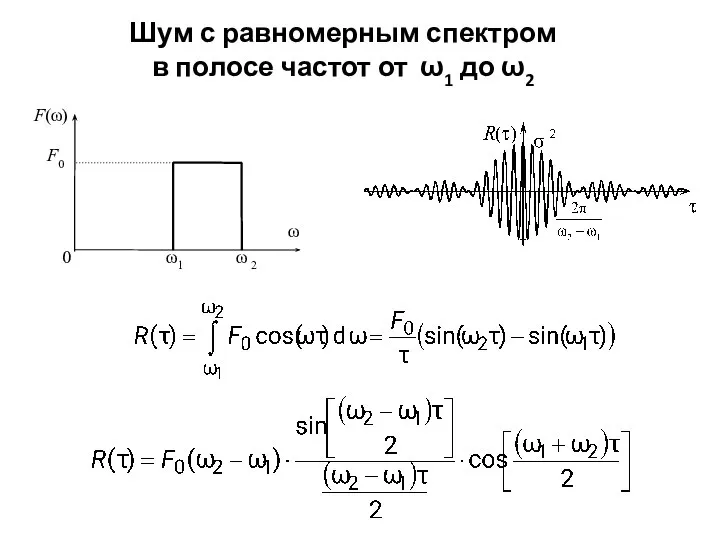
- 17. Шум с равномерным спектром в полосе частот от ω1 до ω2
- 18. Источники шумов в радиотехнических устройствах Тепловой шум формула Найквиста k = 1,38⋅10 –23 Дж/град — постоянная
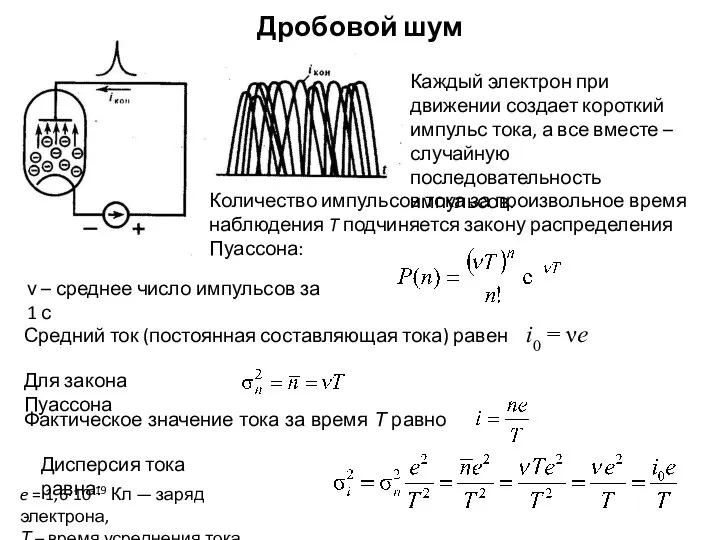
- 19. Дробовой шум Каждый электрон при движении создает короткий импульс тока, а все вместе – случайную последовательность
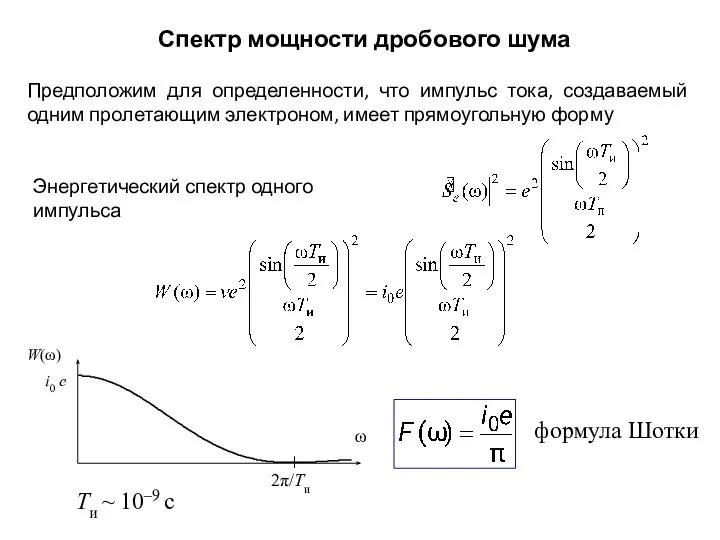
- 20. Спектр мощности дробового шума Предположим для определенности, что импульс тока, создаваемый одним пролетающим электроном, имеет прямоугольную
- 21. Пример: дисперсия дробового шума диода в режиме насыщения при токе i0 = 100 мА и полосе
- 23. Скачать презентацию










 Основы гидравлики
Основы гидравлики Сверлильный станок
Сверлильный станок Производная в физике и технике
Производная в физике и технике Обработка спектров
Обработка спектров svobodnoe_padenie_tel_kopiya
svobodnoe_padenie_tel_kopiya Закон Ома. Светодиоды. Кнопки
Закон Ома. Светодиоды. Кнопки Метод узлового напряжения
Метод узлового напряжения Источники электрической энергии. Системы электроснабжения воздушных судов. Тема 6
Источники электрической энергии. Системы электроснабжения воздушных судов. Тема 6 Последовательное соединение
Последовательное соединение Составные части велосипеда
Составные части велосипеда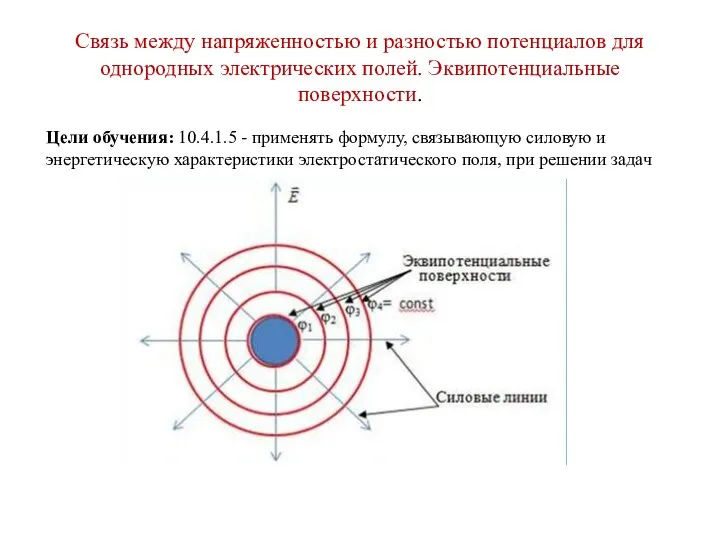 Эквипотенциальные поверхности
Эквипотенциальные поверхности Электростатика. Цели и задачи
Электростатика. Цели и задачи Robust Control of Quantum Systems: Limitations or No Fundamental Limitations?
Robust Control of Quantum Systems: Limitations or No Fundamental Limitations? 2_Волны
2_Волны Алюминий и его сплавы, их характеристика. Деформируемые и литейные сплавы алюминия. Порошковые сплавы. (Лекция 13)
Алюминий и его сплавы, их характеристика. Деформируемые и литейные сплавы алюминия. Порошковые сплавы. (Лекция 13) Статика. Устойчивое равновесие тел
Статика. Устойчивое равновесие тел Презентация_Кинематика криволинейное движение (2)
Презентация_Кинематика криволинейное движение (2) Полезные свойства кавитации
Полезные свойства кавитации Французский язык
Французский язык Презентация на тему Механическая работа и мощность
Презентация на тему Механическая работа и мощность  Физика плазмы
Физика плазмы Строение атома
Строение атома History. Классикалық механиканың негізгін қалаған ғалым
History. Классикалық механиканың негізгін қалаған ғалым Применение скакалки, каната на занятиях физической культуры и внеурочной деятельности
Применение скакалки, каната на занятиях физической культуры и внеурочной деятельности Пузырьковая камера
Пузырьковая камера DZ-3
DZ-3 Презентация по физике "Парогенераторы АЭС" -
Презентация по физике "Парогенераторы АЭС" -  Измерение давления
Измерение давления