Автоматическое управление. Типовая упрощенная структура САУ

Литература
1. Куропаткин П.В. Теория автоматического управления. - М.: Высшая школа, 1973. - 507 с.
2. Теория автоматического управления: учебник для вузов / под ред. А.В. Нетушила. – 2-е изд. - ч.1. - М.: Высш. шк., 1976. – 400 с.
Дополнительная литература
3. Протасов А.П., Рычков В.В. Теория автоматического управления. Учебное пособие по курсу «Теория автоматического управления». - Киров: Изд-во ВятГУ , 2011.-107 с.
4. Ишутинов Д.В., Рычков В.В. Основы работа в System View. – Киров: изд-во ВятГУ, 2008.- 23 с.
5. Рычков В.В. Теория автоматического управления. : учебно-методическое пособие по лабораторным работам и самостоятельной работе. - Киров: ФГБОУ ВПО «ВятГУ», 2014. – 49 с.
6. Рычков В.В. Теория автоматического управления: учебно-методическое пособие по курсовому проекту. - Киров: ФГБОУ ВПО «ВятГУ», 2014. – 55 с.

Лабораторные работы
Методичка.
Развёрнутый лист в клеточку.
Линейка или прямоугольный треугольник (равнобедренный с углами 45 °).
Простой карандаш.
Цветные карандаши.
Резинка или ластик.
Точилка.
Трафарет.
Калькулятор с вычислением lg.

Автоматическим управлением называется процесс поддержания или изменения по заданному закону значений показателей какого-либо процесса за счет подачи на регулятор сигналов, определяемых действительным ходом этого процесса.
Регулируемой величиной в ТАУ называют физическую величину, которую нужно регулировать.
Машины или иные технические устройства, поведением которых управляют, называются объектами управления.
Совокупность устройств, с помощью которых обеспечивается поддержание или изменение по заданному закону регулируемой величины, называется регулятором или управляющим устройством.
Совокупность объекта регулирования и регулятора называется САУ (система автоматического управления).

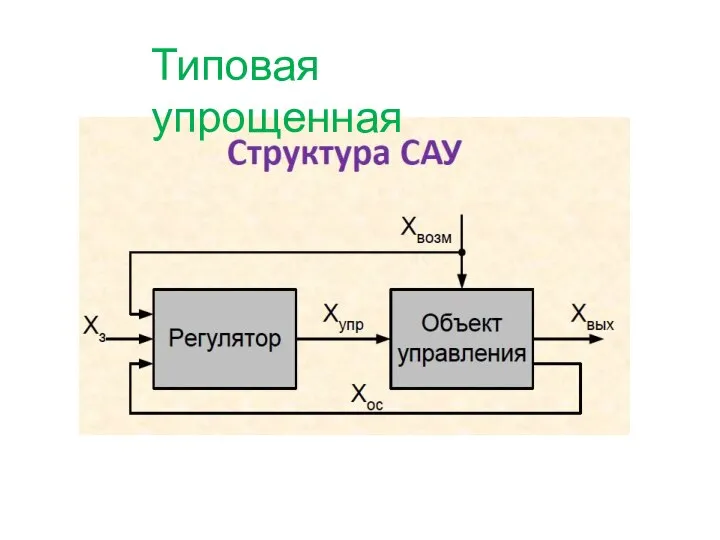
Типовая упрощенная

Отклонение регулируемой величины от заданного значения происходит под действием различных причин или, как их называют в ТАУ, – воздействие. Основными воздействиями, оказываемыми на САУ, являются задающие и возмущающие. Задающие воздействия определяют закон изменения управляемой величины. Возмущающие воздействия, основные и второстепенные, стремятся нарушить требуемую функциональную связь между задающим воздействием и регулируемой величиной. Основные возмущающие воздействия определяются нагрузкой системы. Второстепенные возмущающие воздействия обуславливаются главным образом отклонением параметров системы от их номинальных значений.
1 Типовые воздействия

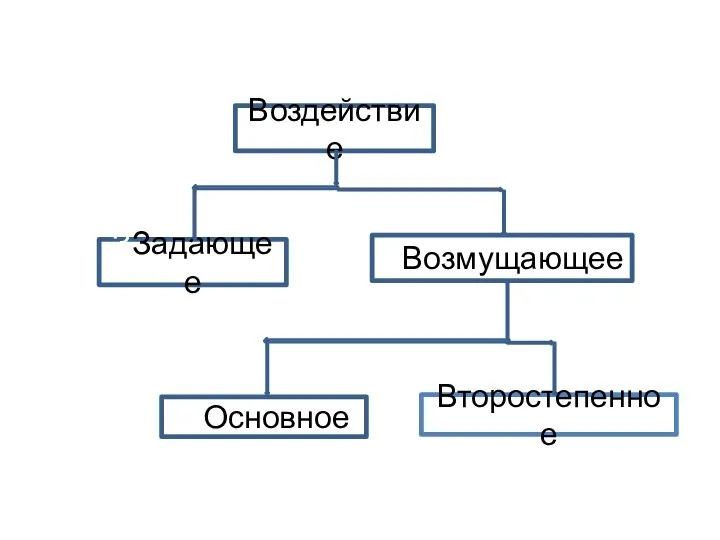
Воздействие
ЗЗадающее
ВВозмущающее
ООсновное
Второстепенное

Характер переходных процессов в результате приложенного к системе воздействия зависит главным образом от структуры и свойств системы, а также от закона изменения воздействия во времени. Для исследуемых динамических свойств системы пользуются типовым воздействием, которое выбирается близким к наиболее неблагоприятному из всего разнообразия возможных реальных воздействий конкретной САУ. К типовым воздействиям относятся:

а) единичный скачок (единичное ступенчатое воздействие) - замыкание или размыкание цепи, приложенное напряжение U(t), I(t) ;
Реакция системы на единичное ступенчатое воздействие называется переходной функцией.
1(t)
1

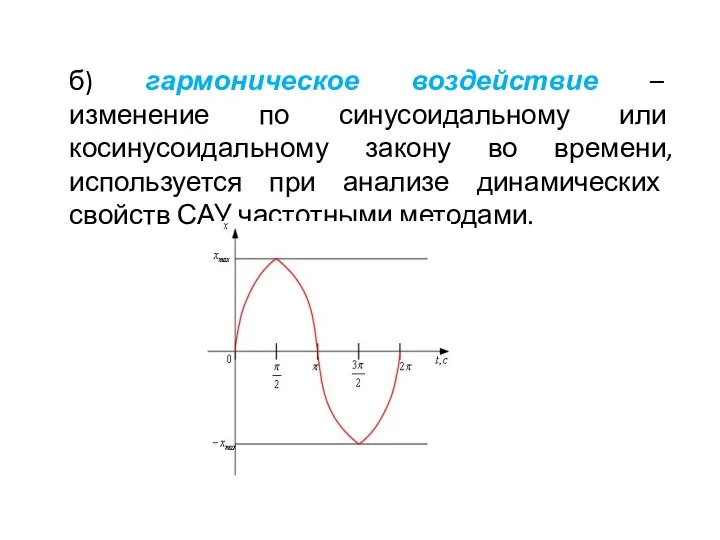
б) гармоническое воздействие – изменение по синусоидальному или косинусоидальному закону во времени, используется при анализе динамических свойств САУ частотными методами.

2 Обратные связи
Задача САУ - обеспечить процесс поддержания или изменения по заданному закону значений показателей какого-либо процесса за счет подачи на регулятор сигналов, определяемых действительным ходом этого процесса. Такая подача сигналов осуществляется при помощи средств обратной связи.
Если же функции управления системы не ставится в зависимость от действительного хода производственного процесса и выполняются по разомкнутому циклу, то такие системы называются разомкнутыми, в отличие от САУ, называемыми замкнутыми.

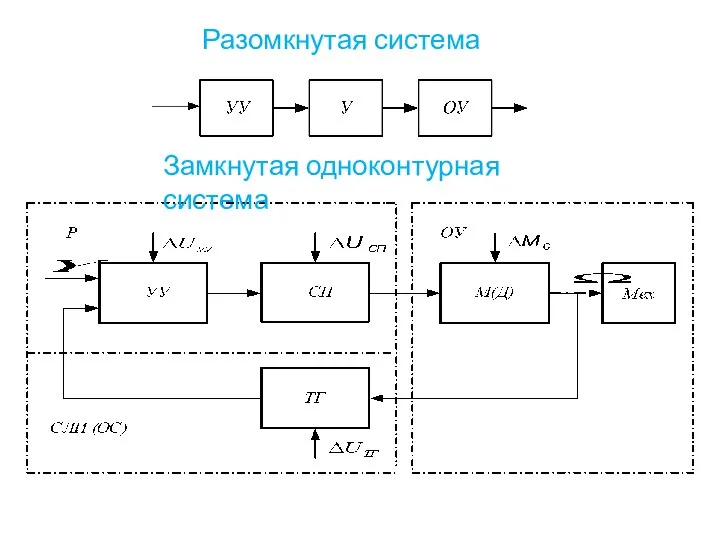
Разомкнутая система
Замкнутая одноконтурная система

Р – регулятор:
УУ – управляющее устройство;
У - усилитель; СП – силовой преобразователь;
ОУ - объект управления:
М(Д) – машина (двигатель);
Мех – механизм:
Ω - скорость;
СЛИ – система логической информации (технической информации):
ТГ – тахогенератор;
Y – задающее воздействие;
ΔМС – основное возмущающее воздействие;
ΔUУУ , ΔUСП , ΔUТГ – второстепенные возмущающие воздействия.

Системы, имеющие одну главную обратную связь, называются одноконтурными. Некоторые САУ, помимо главных ОС, число которых определяется числом регулируемых величин, имеют еще несколько дополнительных (местных). Последние соединяют выход и вход одного или нескольких элементов системы. САУ, имеющие, кроме главной, еще одну или несколько дополнительных обратных связей, называются многоконтурными. В ЭП используется до четырёх контуров: по пути, скорости, по напряжению или э.д.с., по току.

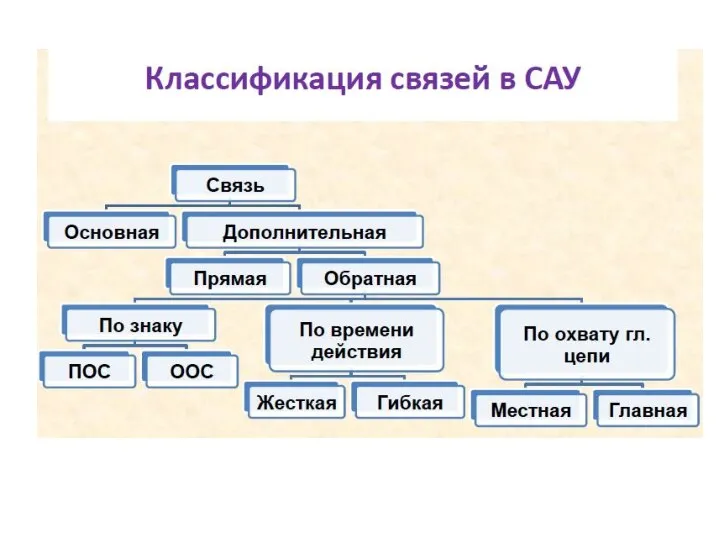
В зависимости от характера передаваемого воздействия О.С. подразделяются на жесткие и гибкие. Жесткие обратные связи действуют как в установившемся, так и в переходном режиме системы. Средства жесткой ОС - различные датчики (измеряющие устройства), передающие сигнал на узел сравнения. Гибкие ОС (ГОС) действуют только в период переходного процесса.

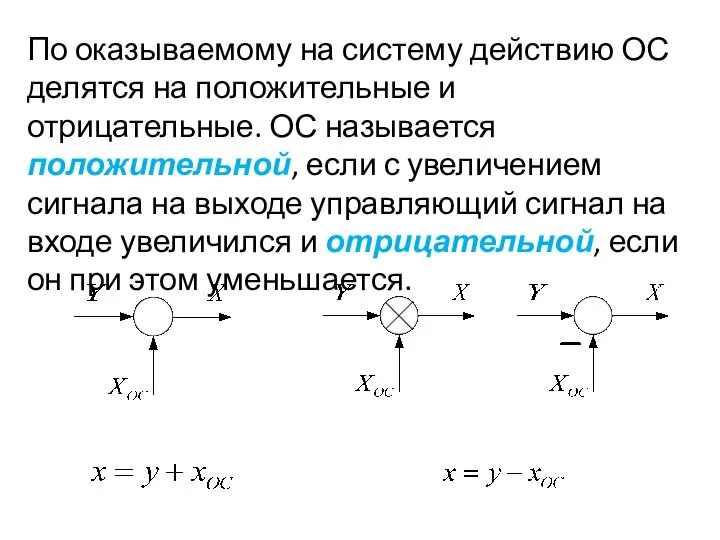
По оказываемому на систему действию ОС делятся на положительные и отрицательные. ОС называется положительной, если с увеличением сигнала на выходе управляющий сигнал на входе увеличился и отрицательной, если он при этом уменьшается.

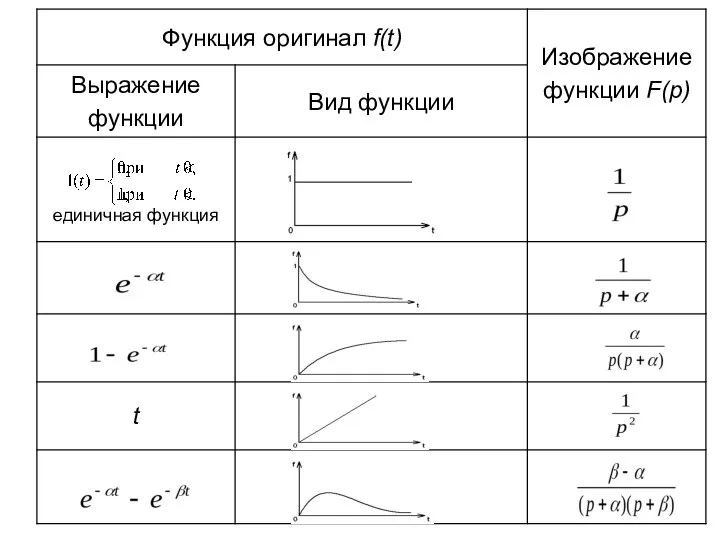
Операторный метод
Сущность операторного метода заключается в том, что расчет переходного процесса переносится из области функций действительной переменной (времени t) в область функций комплексного переменного . При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор p. Это существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраической.
Переход из области действительного переменного в область функций комплексного переменного осуществляется с помощью прямого преобразования Лапласа. После этого решаются алгебраические уравнения относительно изображений искомых функций. Полученное решение алгебраических уравнений обратным преобразованием Лапласа переносится в область действительного переменного.

Прямое преобразование Лапласа определяется уравнением
, (1)
где f(t) – функция действительного переменного t, определенная при t>0.
Функция F(p), определяемая уравнением (1), называется изображением по Лапласу, а функция f(t) в (1) – оригиналом.
Обратное преобразование Лапласа определяют из решения
.
Следовательно, оригинал и изображение представляют собой пару функций действительного f(t) и комплексного F(p) переменного, связанных преобразованием Лапласа и поставленных друг другу в строгое соответствие.

Для сокращения записи преобразований (1) используют следующую символику:
,
где L – оператор Лапласа.
В дальнейшем для определенности будем использовать знак соответствия.

Рассмотрим некоторые свойства преобразования Лапласа, называемые также теоремами.
Теорема о сложении или линейность преобразования
.
Теорема о дифференцировании
3. Теорема об интегрировании
4. Теорема запаздывания

Пользуясь основными свойствами преобразования Лапласа, можно получить основные законы теории цепей в операторной форме.
Рассмотрим, например, последовательный RLC – контур (рис.), находящийся при ненулевых начальных условиях:
.
Уравнение равновесия напряжений для этого контура согласно второго закона Кирхгофа имеет вид:
.

Применив к прямое преобразование Лапласа и учитывая свойства линейности дифференцирования и интегрирования оригинала или выражения для напряжений на резистивном индуктивном и емкостном элементах, получим:
.
Второй закон Кирхгофа в операторной форме:
.
алгебраическая сумма операторных падений напряжений на всех участках замкнутого контура равна алгебраической сумме операторных ЭДС, включенных в этот контур.

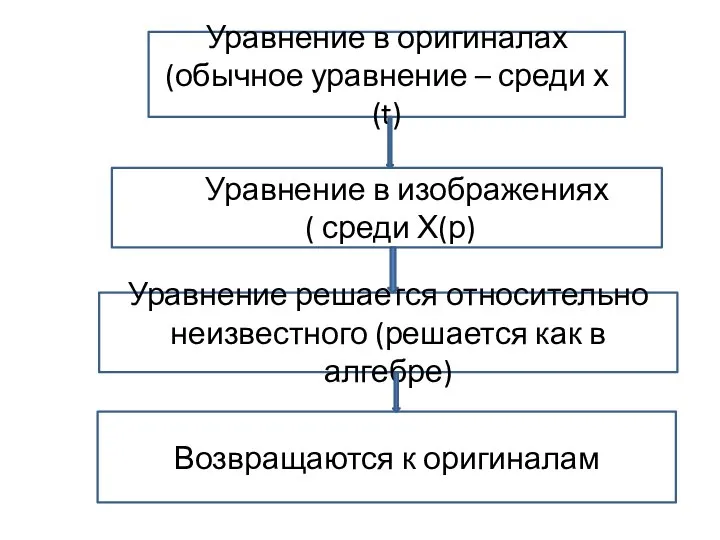
Алгоритм анализа переходных процессов операторным методом.
Расчет переходного процесса операторным методом предусматривает следующий порядок операций:
- вычерчивается исходная расчетная схема замещения цепи и определяются начальные условия коммутации;
- все известные электрические величины и параметры изображаются в операторной форме (сложение функции – с помощью таблиц оригиналов и изображений) и осуществляется переход к операторной схеме замещения цепи;
- на основе законов Кирхгофа в операторной форме в соответствии с выбранным методом расчета цепи после ее коммутации составляется система операторных уравнений с учетом начальных условий, которая решается относительно изображений искомых переходных токов и напряжений;
- получение изображения искомых переходных токов и напряжений преобразуются либо к табличным, либо к виду, удобному для применения теоремы разложения, и определяются оригиналы (переходные токи и напряжения);
- производится анализ характера переходного процесса.

Уравнение в оригиналах (обычное уравнение – среди х(t)
УУУравнение в изображениях
( среди Х(р)
Уравнение решается относительно неизвестного (решается как в алгебре)
Возвращаются к оригиналам

1 Динамика объектов
Уравнение динамики объектов
Пусть дана система
Если получить систему дифференциальных уравнений, составленных для каждого элемента САУ относительно какой-либо одной регулируемой величины х(t)=хВЫХ(t) по отношению к отклонению х(t)=хВХ(t) и к возмущающему воздействию f (t), то в результате получим дифференциальные уравнения с постоянными коэффициентами следующего вида:

где − постоянные коэффициенты.
Уравнение носит название общего дифференциального уравнения САУ или уравнения движения САУ.

Применяя к дифференциальному уравнению при нулевых начальных условиях преобразование Лапласа, запишем это уравнение в операторной форме:
где XВЫХ(p); ХВХ(p) и F(p) – изображения соответственно функций xВЫХ(t); хВХ(t) и f(t).

1.1 Понятие о передаточной функции
Передаточной функцией САУ по задающему воздействию называется отношение операторного изображения выходной величины САУ к операторному изображению входной величины САУ при нулевых начальных условиях, т.е.:

передаточной функцией САУ по возмущающему воздействию называют отношение операторного изображения выходной величины к операторному изображению возмущающего воздействия при нулевых начальных условиях

Т.к. при записи уравнений линейной САУ в операторной форме дифференциальные уравнения становятся алгебраическими, то с ними можно оперировать совершенно так же, как с линейными уравнениями для установившегося режима.
Обозначим соответственно
- полиномы
степени от .
Тогда передаточная функция по задающему воздействию равна
где - характеристическое уравнение.

Найдём переходную функцию при входном единичном ступенчатом воздействии
хВХ(t)=1(t) , тогда ХВХ(р)= .
.
Вычислим
Перейдём к оригиналу.
где рi – корни уравнения Gn+1(p)=0.

1.2 Частотные характеристики

Совместное изменение амплитуды и фазы выходной величины от частоты можно получить, если представить синусоидальные функции в комплексной форме:
Если взять отношение выходной величины ХВЫХ(jω) к входной величине ХВХ(jω), то получим
- показательная форма записи комплексного числа

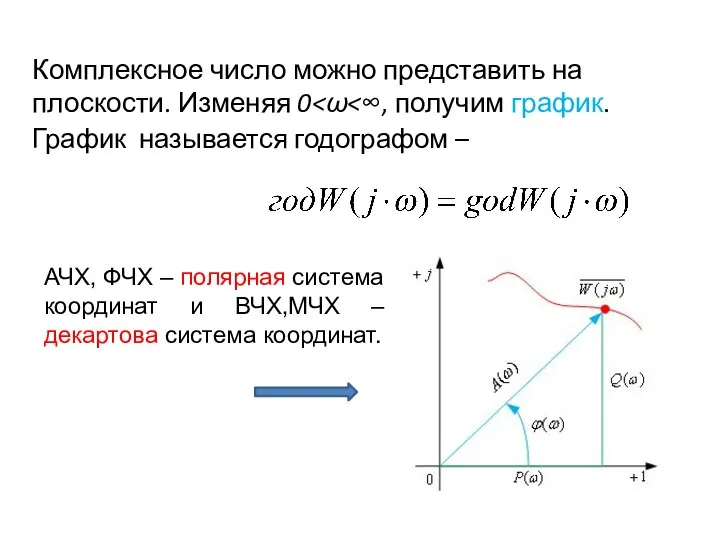
Комплексная функция W(jω) называется комплексным коэффициентом передачи САУ или амплитудно-фазовой частотной характеристикой (АФЧХ) САУ. Модуль этой функции представляет собой амплитудно-частотную характеристику (АЧХ), а аргумент – фазо-частотную характеристику (ФЧХ).
В общем случае W(jω) может быть представлен в виде числа
алгебраическая форма записи комплексного числа
где P(ω) – называется вещественной частотной характеристикой САУ (ВЧХ);
Q(ω) – называется мнимой частотной характеристикой САУ (МЧХ).

Между собой ВЧХ, МЧХ и АЧХ, ФЧХ связаны

График называется годографом –
АЧХ, ФЧХ – полярная система координат и ВЧХ,МЧХ – декартова система координат.
Комплексное число можно представить на плоскости. Изменяя 0<ω<∞, получим график.

Логарифмические частотные характеристики
В практических расчетах наряду с использованием АФЧХ широко используются так называемые логарифмические амплитудные фазовые частотные характеристики ЛАФЧХ или просто логарифмические частотные характеристики. При этом различают логарифмические амплитудные частотные характеристики (ЛАЧХ) и логарифмические фазовые частотные характеристики (ЛФЧХ).
ЛАЧХ называют зависимость L(ω)=lgА(ω) от lg (ω),
ЛФЧХ называют зависимость ϕ(ω)от lg (ω).

При построении ЛЧХ по оси абсцисс откладывается частота в логарифмическом масштабе
Интервал частот, кратный 10, называется декадой.

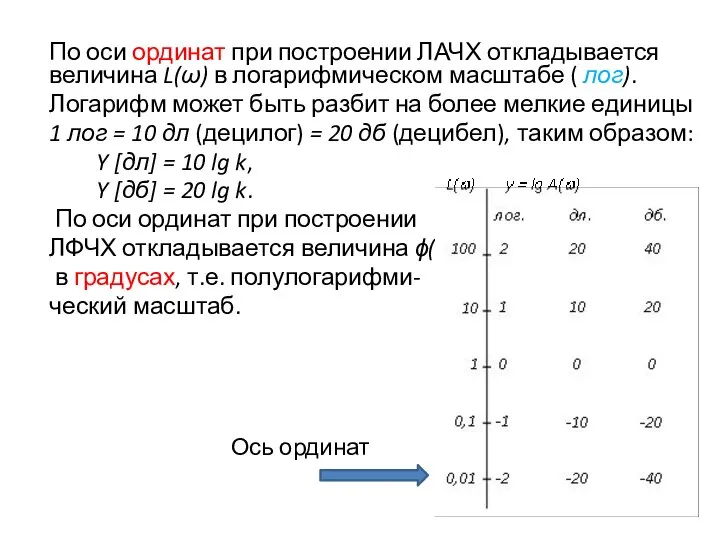
По оси ординат при построении ЛАЧХ откладывается величина L(ω) в логарифмическом масштабе ( лог).
Логарифм может быть разбит на более мелкие единицы
1 лог = 10 дл (децилог) = 20 дб (децибел), таким образом:
Y [дл] = 10 lg k,
Y [дб] = 20 lg k.
По оси ординат при построении
ЛФЧХ откладывается величина ϕ(ω)
в градусах, т.е. полулогарифми-
ческий масштаб.
Ось ординат