Содержание
- 2. Метод биомеханики ‒ системный анализ и системный синтез движений на основе количественных характеристик, в частности кибернетическое
- 3. Система движений как целое ‒ не просто сумма её составляющих частей. Части системы объединены многочисленными взаимосвязями,
- 4. При изучении движений в процессе развития системного анализа и синтеза в последние годы все шире применяется
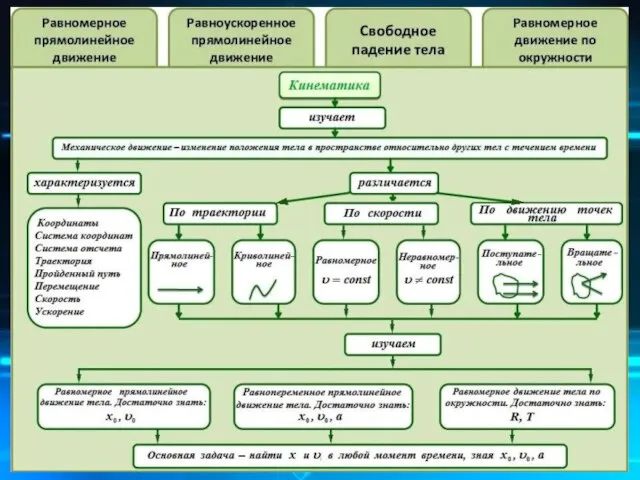
- 5. КИНЕМАТИКА
- 6. Относительность движения
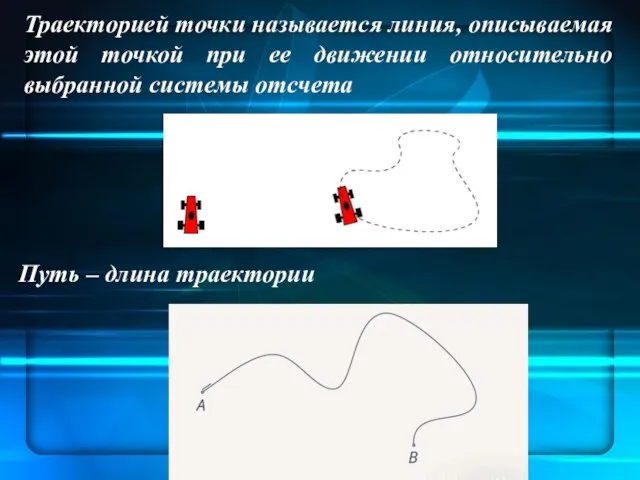
- 7. Путь ‒ длина траектории Траекторией точки называется линия, описываемая этой точкой при ее движении относительно выбранной
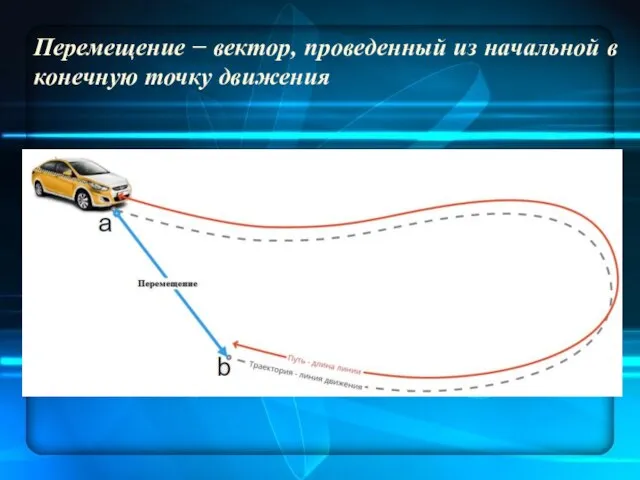
- 8. Перемещение − вектор, проведенный из начальной в конечную точку движения
- 9. В зависимости от формы траектории различают прямолинейное и криволинейное движения точки В общем случае траектория точки
- 10. Скорость Для характеристики направления и быстроты движения в механике вводится векторная физическая величина, называемая скоростью Средней
- 11. Средней скорость направлена так же, как вектор перемещения Δr. Так как |Δr| ≤ ΔS, где ΔS
- 12. Мгновенная линейная скорость – физическая величина равная пределу, к которому стремится отношение элементарного перемещения Δr за
- 13. Величину пройденного точкой пути можно представить графически площадью фигуры ограниченной кривой υ = f(t) прямыми t
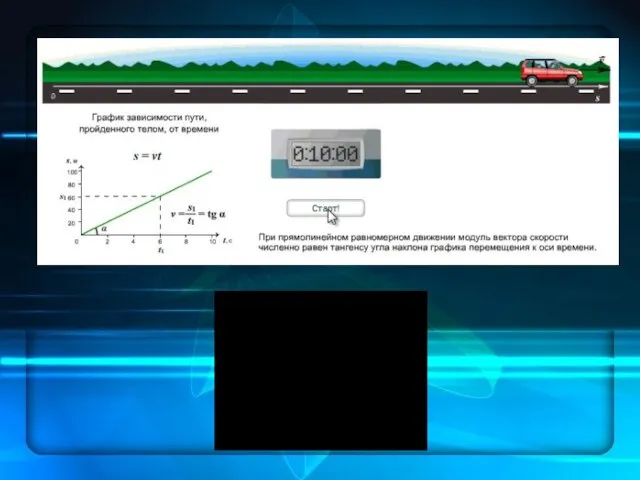
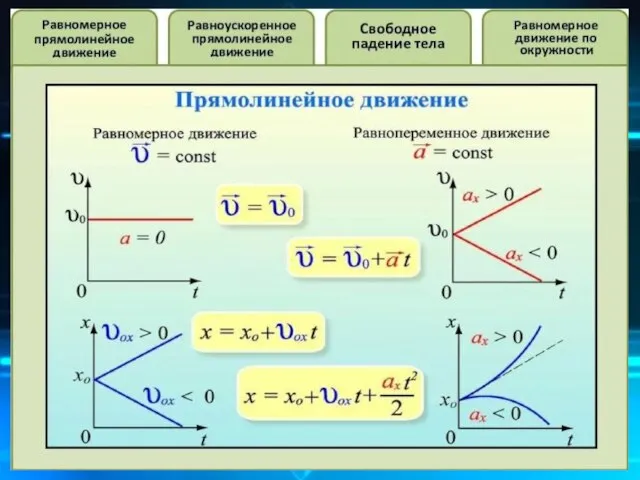
- 14. Прямолинейное равномерное движение Прямолинейным равномерным движением называется движение при котором материальная точка, двигаясь по прямой, за
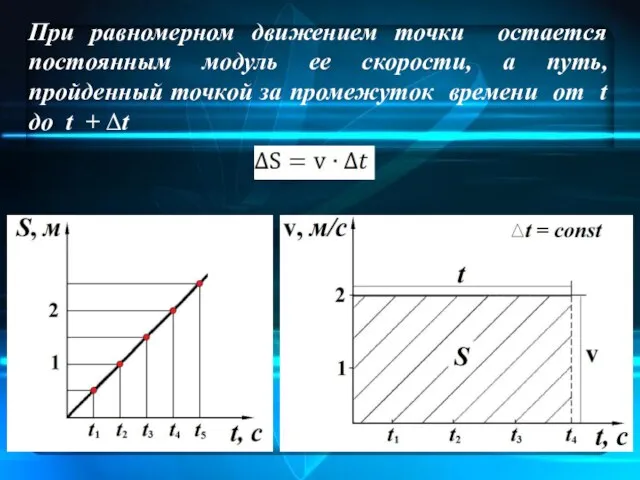
- 16. При равномерном движением точки остается постоянным модуль ее скорости, а путь, пройденный точкой за промежуток времени
- 17. Ускорение Быстроту изменения скорости характеризует ускорение. Если в начальный момент времени t0 = 0 тело имеет
- 18. При движении точки мгновенная скорость может меняться как по величине, так и по направлению. Вектор Δυ/Δt,
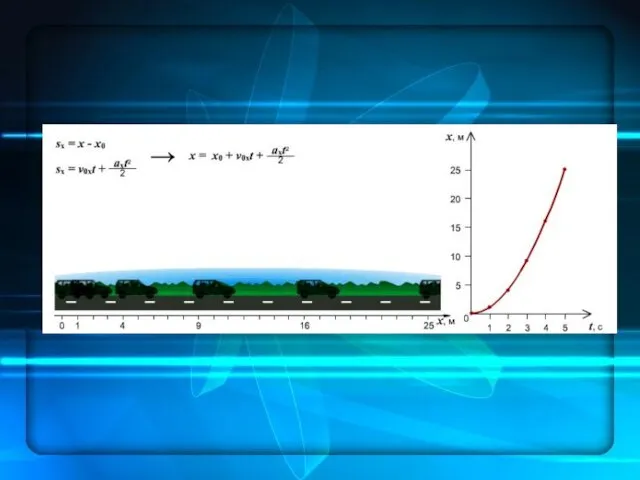
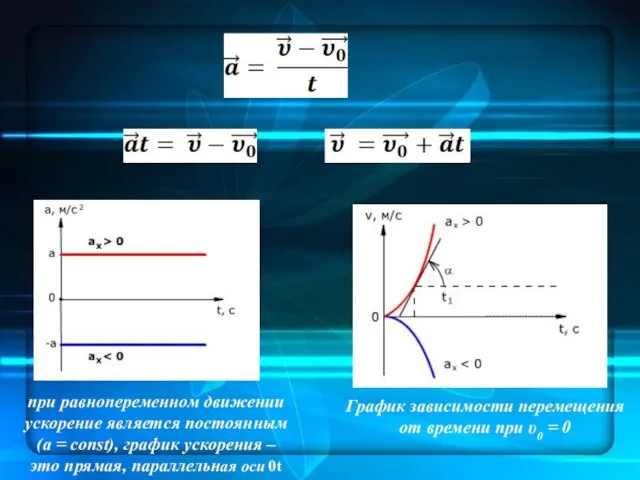
- 20. Прямолинейное равнопеременное движение Движение материальной точки, при котором ее скорость за любые промежутки времени увеличивается или
- 21. График зависимости перемещения от времени при υ0 = 0 при равнопеременном движении ускорение является постоянным (a
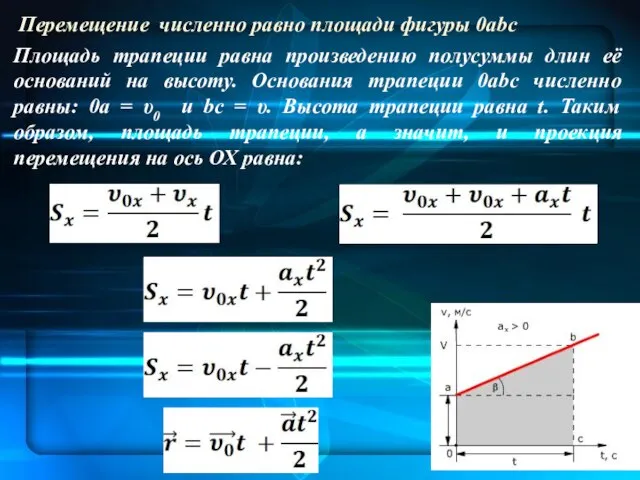
- 22. Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны: 0a
- 23. Так как положение материальной точки (тела) в любой момент времени определяется суммой начальных координат и проекции
- 24. Существует несколько удобных соотношений, описывающих движение тела с постоянным ускорением. Пусть составляющая скорости в направлении этого
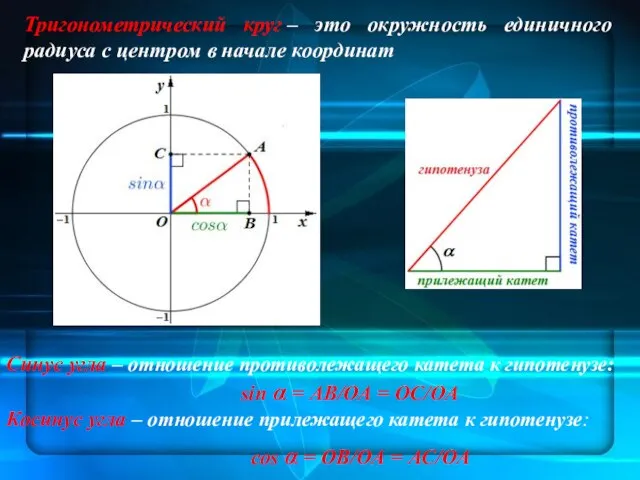
- 25. Тригонометрический круг – это окружность единичного радиуса с центром в начале координат Синус угла – отношение
- 26. Некоторые математические операции над векторами Пусть υ1 и υ2 ‒ два вектора, приложенные к одной точке
- 27. Скалярное произведение двух векторов, например векторов a и b, называется скалярная величина, равная произведению модулей этих
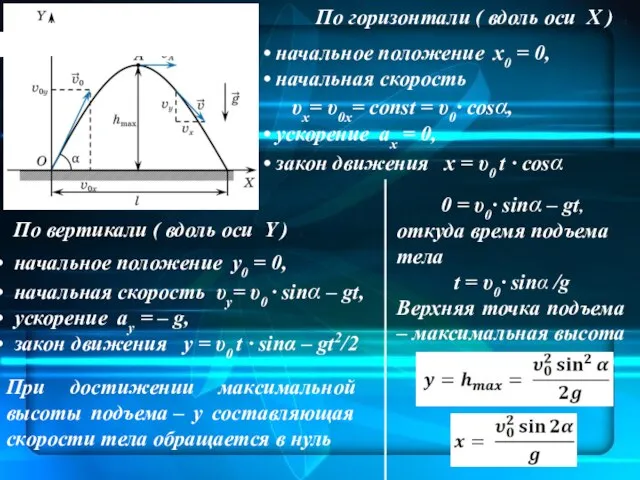
- 28. По горизонтали ( вдоль оси X ) ): начальное положение x0 = 0, начальная скорость υx=
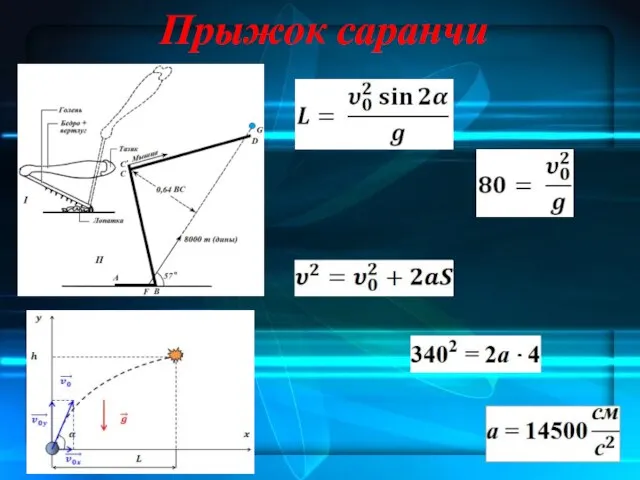
- 29. Прыжок саранчи
- 30. А В
- 31. Криволинейное движение. Движение по окружности. Движение по окружности ‒ простейший случай криволинейного движения тела. Когда тело
- 32. Движение точки по траектории может быть: ускоренным, если модуль скорости возрастает с течением времени; равноускоренным, если
- 33. При векторном способе движение точки задается законом изменения радиуса-вектора во времени При координатном способе движение точки
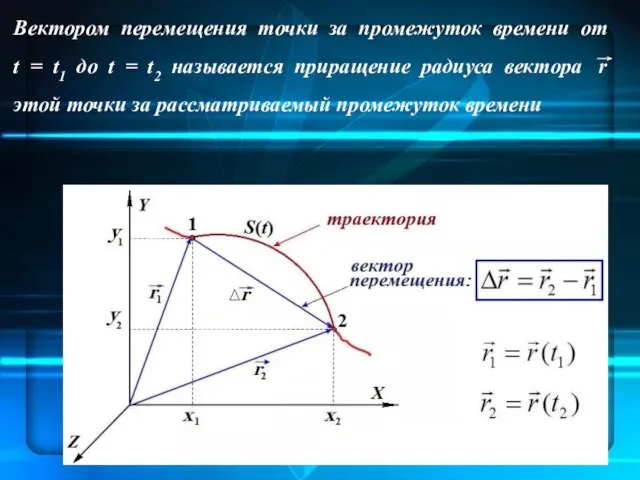
- 34. Вектором перемещения точки за промежуток времени от t = t1 до t = t2 называется приращение
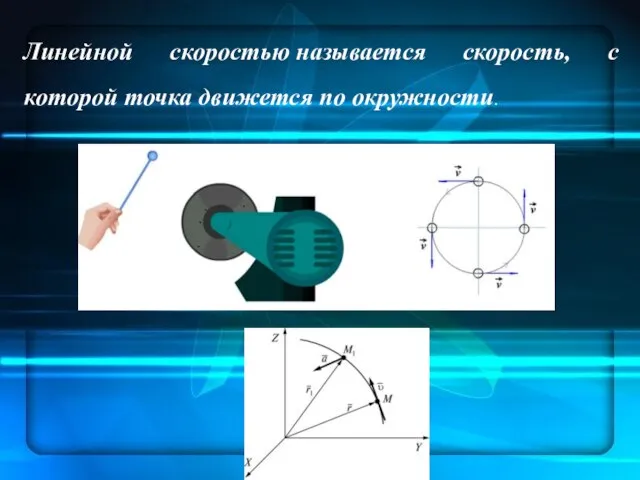
- 35. Линейной скоростью называется скорость, с которой точка движется по окружности.
- 36. Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый
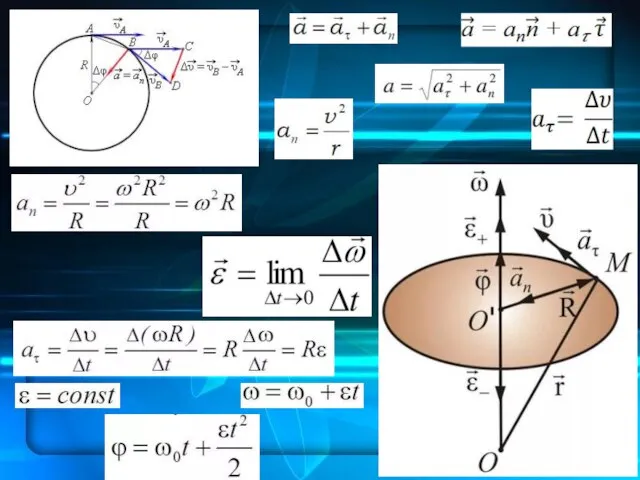
- 38. Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой
- 40. Частота вращения показывает, сколько оборотов совершает за единицу времени материальная точка (тело), равномерно вращающееся с угловой
- 41. В общем случае траектория точки ‒ пространственная кривая, а ускорение а лежит в соприкасающейся плоскости. Плоскость,
- 42. Нормаль ‒ прямая, перпендикулярная касательной прямой к кривой, касательной плоскости к поверхности Вектор нормали n к
- 43. Координатный способ задания движения точки При координатном способе находим: разложение вектора скорости на координатные оси скорость
- 44. В общем случае ускорение не совпадает по направлению с вектором скорости. Вектор ускорения а может быть
- 49. Точка движется по оси Ох по закону x = 5 + 4t – 2t2 (м). Определить
- 51. Скачать презентацию
































 Электрический двигатель постоянного тока. Лабораторная работа
Электрический двигатель постоянного тока. Лабораторная работа Магнитное поле. Магнитное поле прямого тока. Магнитные линии
Магнитное поле. Магнитное поле прямого тока. Магнитные линии Твой звездный час. Интеллектуальная игра тепловые явления
Твой звездный час. Интеллектуальная игра тепловые явления Равенство работ при использовании простых механизмов. Золотое правило механики
Равенство работ при использовании простых механизмов. Золотое правило механики Силы в природе
Силы в природе физические величины измерение физических величин 6 класс презентация (1)
физические величины измерение физических величин 6 класс презентация (1) Явления электромагнитной индукции
Явления электромагнитной индукции Синхронизаторы. Конструкция инерционного синхронизатора
Синхронизаторы. Конструкция инерционного синхронизатора Итоговая контрольная работа
Итоговая контрольная работа Механическая работа. Мощность. Самостоятельная работа
Механическая работа. Мощность. Самостоятельная работа Космология Ньютона. Часть 2. Физика космоса
Космология Ньютона. Часть 2. Физика космоса Работа, мощность силы. Кинетическая энергия. Лекция 9
Работа, мощность силы. Кинетическая энергия. Лекция 9 Одиниці вимірювання маси
Одиниці вимірювання маси 8e84aba704c3488a88a3d72ef17c3ee4
8e84aba704c3488a88a3d72ef17c3ee4 Электричество и магнетизм
Электричество и магнетизм Итоговый тест по курсу физии
Итоговый тест по курсу физии Решение задач по теме; Законы сохранения
Решение задач по теме; Законы сохранения Предыстория радиотехники. Лекция 3
Предыстория радиотехники. Лекция 3 Проводники и диэлектрики в электрическом поле
Проводники и диэлектрики в электрическом поле Изобретение радио и принципы радиосвязи
Изобретение радио и принципы радиосвязи Закон всемирного тяготения
Закон всемирного тяготения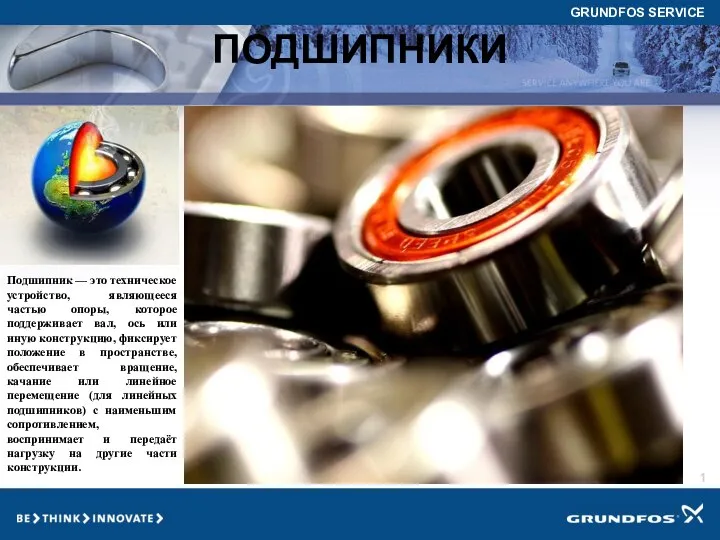 Подшипники
Подшипники Ременные передачи
Ременные передачи Логарифмы в физике
Логарифмы в физике Фотоэффект. Самостоятельная работа
Фотоэффект. Самостоятельная работа Электрический ток в вакууме. Электронные пучки. Электронно-лучевая трубка
Электрический ток в вакууме. Электронные пучки. Электронно-лучевая трубка Устройство швейной машины Yamata
Устройство швейной машины Yamata Электрическая цепь. Электрическая схема
Электрическая цепь. Электрическая схема